9. Funktionsvärden

Bestäm funktionsvärdena för funktionen $f(x)=x^2-2$ då $x=2$ och då $x=2,5$.

Värdet av en funktion får vi genom att placera in värdet på variablens plats.

Exempel 1 Bestäm funktionsvädet för $f(x)=3x-5$ då $x$ får värdena $-3$, $1$ och $5$.

Lösning

Vi får att

$\begin{array}{rl} -3: & f(-3)=3(-3)-5=-9-5=-14 \\ 1: & f(1)=3\cdot 1-5=3-5=-2 \\ 5: & f(5)=3\cdot 5 -5 = 15-5=10\\ \end{array}$

Exempel 2 Låt $g(x)=2x-6$.

Bestäm funktionsvärdet för $x=4$.
Den punkt som ger funktionsvärdet 4.

Lösning

Vi får att $g(4)=2\cdot 4 -6 = 8-6=2$.
Här söker vi den $x$-koordinat som ger att funktionsvärdet är 4, alltså $g(x)=4$.

Vi får att

$\begin{array}{rcll} 4 & = & 2x-6 & \mid +6\\ 4+6 & = & 2x \\ 2x & = & 10 & \mid /2\\ x & = & \dfrac{10}{2}=5 \\ \end{array}$

$x$-koordinaten 5 ger funktionsvärdet 4.

Nollställen för en funktion

Funktionens nollställen är de punkter där grafen skär $x$-axeln. Det sker då $f(x)=0$, som betyder att $y$-koordinaten har värdet 0. När vi söker nollställen svarar vi antingen som en punkt eller som en $x$-koordinat.

Exempel 3 Bestäm nollstället för funktionen $h(x)=4x-8$.

Lösning

Vi löser ekvationen

$\begin{array}{rcll} 4x -8 & = & 0 & \mid +8\\ 4x & = & 8 & \mid /4 \\ x & = & \dfrac{8}{4}=2 \end{array}$

Nollstället är $(2,0)$.

Exempel 4 Bestäm nollställena för $f(x)=2x^2-6x$.

Lösning

Vi löser ekvationen

$\begin{array}{rcll} 2x^2-6x & = & 0 & \mid \text{ Utbrytning}\\ 2x(x-3) & = & 0 & \mid\text{ Nollregel} \\ \end{array}$

$2x=0 \Leftrightarrow x=0$ eller $x-3=0 \Leftrightarrow x=3$.

Vi har två nollställen, $x=0$ och $x=3$.

Funktioner klassificerar vi som antingen jämna eller udda genom att se på den högsta exponenten för funktionen. Jämna funktioner är funktioner vars högsta exponent är ett jämt tal: $2, 4, 6, 8 \ldots$ och udda funktioner har ett udda tal: $1, 3, 5, 7, \ldots$.

Funktionsvärden och nollställen på GeoGebra

Uppgifter

Bestäm följande värde genom att avläsa från grafen.
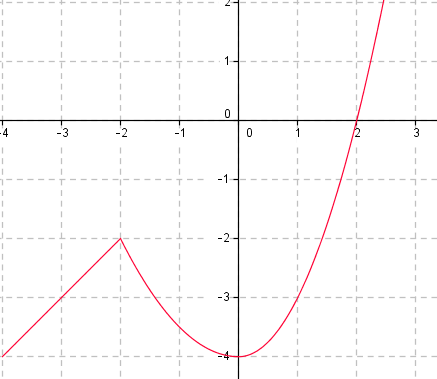
1. $f(1)$
  
  -3
2. $f(-2)$
  
  -2
3. $f(x)=0$
  
  $f(x)=0$ då $ x = 2$.
4. $f(x)=-4$
  
  $f(x)=-4$ då $x = -4$ eller $ x =0$.
Rita grafen av funktionen $f(x)=x^3+1$ på GeoGebra och svara på följande frågor.
1. Bestäm nollstället för funktionen.
  
  Nollstället är i punkten $x=-1$ och $ x=0 $.
2. $f(1)$
  
  2
3. $f(x)=1$
  
  $f(x)=1$ då $ x = 0 $.
Låt $h(x)=-2x+3$. Bestäm grafiskt genom att rita funktionen på GeoGebra.
1. vädet för funktionen $h$ då $x=2$.
  
  -1
2. vädet för funktionen $h$ då $x=0$
  
  3
3. nollställena för funktionen $h$
  
  Då $x=\dfrac{3}{2}$.
Bestäm funktionsvärden för $f(x)=3x-5$.

Räkna, ersätt $x$ med siffrorna i uttrycket.

Se exempel 1 och 2. Se dessutom Funktionsvärden och nollställen med GeoGebra.
1. $f(0)$
  
  $f(0)=3\cdot 0 - 5 = -5$
2. $f(2)$
  
  1
3. $f(10)$
  
  25
4. $f(2000)$
  
  5995
Låt $g(x)=2x^2-4x+7$. Bestäm
1. $g(-4)$
  
  55
2. $g(-1)$
  
  13
3. $g(0)$
  
  7
4. $g(25)$
  
  1157
För vilket värde på $x$ får funktionen $h(x)=6x-5$ värdet 3?

Se exempel 2 och Funktionsvärden och nollställen med GeoGebra.

$\begin{array}{rcll} 6x-5 & = & 3 & \mid +5 \\ 6x & = & 8 & \mid /6 \\ x & = & \dfrac{8}{6} = \dfrac{4}{3} \\ \end{array}$
För vilket värde på $x$ får funktionen $g(x)=2x^2-8$ värdet $-6$?

Vi löser ekvationen

$\begin{array}{rcll} 2x^2-8 & = & -6 & \mid +8 \\ 2x^2 & = & 2 & \mid /2 \\ x^2 & = & \dfrac{2}{2}=1 & \mid \sqrt{\;} \\ x & = & \pm 1\\ \end{array}$

Då $x = \pm 1$.
Bestäm nollställena för $f(x)=4x-2$.

Se exempel 3 och Funktionsvärden och nollställen med GeoGebra.

$\begin{array}{rcll} 4x-2 & = & 0 & \mid +2 \\ 4x & = & 2 & \mid /4 \\ x & = & \dfrac{2}{4} = \dfrac{1}{2} \\ \end{array}$
Bestäm nollställena för $f(x)=\dfrac{3}{4}x+\dfrac{2}{3}$.

Vi söker de punkter där funktionsvärdet får värdet 0.

Se exempel 3, 4 och Funktionsvärden och nollställen med GeoGebra.

$\begin{array}{rcll} \dfrac{3}{4}x+\dfrac{2}{3} & = & 0 & \mid -\dfrac{2}{3} \\ \\ \dfrac{3}{4}x & = & -\dfrac{2}{3} & \mid \cdot \dfrac{4}{3} \\ \\ \dfrac{3}{4}x\cdot \dfrac{4}{3} & = & -\dfrac{2}{3} \cdot \dfrac{4}{3} \\ \\ x & = & -\dfrac{8}{9} \\ \end{array}$
Bestäm nollställena för $f(x)=5x^2-5$.

Se exempel 4 och Funktionsvärden och nollställen med GeoGebra.

$\begin{array}{rcll} 5x^2-5 & = & 0 \\ 5x^2 & = & 5 & \mid /5 \\ x^2 & = & 1 & \mid \sqrt{\quad} \\ x & = & \sqrt{1} = \pm 1 \\ \end{array}$

Funktionens nollställen är $x=-1$ och $x=1$.
Bestäm nollställena för $f(x)=\dfrac{2}{5}x^2-\dfrac{2}{3}x$.

Bryt ut det gemensamma och fortsätt med nollregeln.

Se exempel 4 och Funktionsvärden och nollställen med GeoGebra.

$\begin{array}{rcll} \dfrac{2}{5}x^2-\dfrac{2}{3}x & = & 0 \\ \\ x(\dfrac{2}{5}x -\dfrac{2}{3}) & = & 0 & \mid \text{Vi bryter ut det gemensamma och tillämpar nollregeln.}\\ \\ \end{array}$

Nu gäller att

$x= 0$ eller $\dfrac{2}{5}x-\dfrac{2}{3}=0$.

$\begin{array}{rcll} \dfrac{2}{5}x-\dfrac{2}{3} & = & 0 \\ \\ \dfrac{2}{5}x & = & \dfrac{2}{3} & \mid \cdot \dfrac{5}{2} \\ \\ \dfrac{2}{5}x\cdot \dfrac{5}{2} & = & \dfrac{2}{3}\cdot \dfrac{5}{2} \\ \\ x & = & \dfrac{5}{3} \end{array}$

Nollställena är $x=0$ och $x=\dfrac{5}{3}$.
Låt $M(a)=a^3+3a^2-2a+5$. Bestäm funktionsvärdet då
1. $a=2$
  
  $M(2) = 2^3 + 3\cdot 2^2 - 2\cdot 2 + 5 = 8+3\cdot 4-4+5 =21$
2. $a=-3$
  
  $M(-3)=(-3)^3 + 3 \cdot (-3)^2-2\cdot (-3) + 5 = -27+3\cdot 9+4+5 = 11$
Van Praag och Frijters gjorde 1999 en studie kring vad människor vill tjäna som lön. De kom fram att för varje dollar som man får i lön vill man egentligen ha 1,4 gånger mera.
Van Praag och Frijters, 1999
1. Skapa en funktion som anger den lön som en person vill ha.
  
  Eftersom man vill ha 1,4 gånger sin lön är funktionen $ f(x)= 1,4x $.
2. Eftersom 1 $ nästan är 1 € kan vi utnyttja funktionen för att bestämma följande.
  Medianlönen i Finland år 1999 var 3 140 €. Vilken summa vill man då egentligen ha?
  
  https://www.tilastokeskus.fi/tup/suoluk/suoluk_palkat.html, 2020
  
  Vi får $ f(3140) = 1,4 \cdot 3140 = 4396 $ €.
3. Hur stor lön har de personerna som drömmer om en lön som är 5 000 €?
  
  Vi får ekvationen $ f(x) = 5000 $, alltså $ 1,4x = 5000 $ som har lösningen $ x = 3571,42\ldots $.
  
  Alltså 3571 €.
Schor undersökte 1999 sambandet med hur mycket människor tittar på tv och hur mycket extra hushåller spenderar pengar. Hon kom fram till att för varje extra timme som människor tittar på tv spenderar de 4 $ extra per vecka.
Schor, 1999

I Finland såg över 4-åringar år 2019 i medeltal på 162 minuter tv.

https://www.finnpanel.fi/tulokset/tv/vuosi/katsaikakan/viimeisin/
1. Skapa en funktion som anger hur mycket extra man spenderar beroende på sitt tv-tittande. Du kan arbeta med 160 minuter.
  
  160 minuter är $ \dfrac{160}{60} = 2\dfrac{2}{3} $ timmar.
  
  Eftersom man spenderar 4 $ extra per timme över medeltalet får vi funktionen $ f(x)= 4(x - \dfrac{8}{3}) $ eller $ f(x)= 4(x - 2\dfrac{2}{3}) $.
2. Hur mycket extra spenderar en familj som ser på 4,5 timmar tv per vecka?
  
  Vi får $ f(4,5) = 4 \cdot (4,5 - \dfrac{8}{3}) = 7,33 $ €.
3. Hur många timmar tv per vecka ser den familj som spenderar 20 $ mera?
  
  Vi får ekvationen $ f(x) = 20 $, alltså $ 4(x - \dfrac{8}{3}) = 20 $ som har lösningen $ x = 7,66\ldots $.
  
  Alltså 7 timmar 40 minuter per dygn.

Bestäm om funktionen är jämn eller udda.

Påstående	Jämn funktion	Udda funktion
$f(x)=3x^3-x$
$g(x)=-x^2+4$
$h(x)=x^2+3x-1$
$i(x)=x^5-6x^4-x$
$j(x)=x^7-4x^6-3x+7$
$k(x)=(x-2)^2$

Se slutet av teorin.

Påstående	Jämn funktion	Udda funktion
$f(x)=3x^3-x$
$g(x)=-x^2+4$
$h(x)=x^2+3x-1$
$i(x)=x^5-6x^4-x$
$j(x)=x^7-4x^6-3x+7$
$k(x)=(x-2)^2$

Hur skiljer sig en jämn funktion från en udda funktion? Använd dig av GeoGebra appletten som finns nedan och ändra på gradtalet för funktionen genom att dra i glidaren för $n$.

Se slutet av teorin och det som du lärde dig i uppgiften ovan.

Jämna funktioner, med exponenten $2, 4, 6, \ldots$ ser nästan alla likadana ut. De påminner om parabeln, betyder att de avtar, sedan händer det något och sedan är funktionen växande.

Udda funktioner, med exponenten $1, 3, 5, \ldots$. De igen påminner om $f(x)=x$ och $g(x)^3$. De växer hela tiden men kan avta vid något intervall.

Påstående	Jämn funktion	Udda funktion
\(f(x)=3x^3-x\)
\(g(x)=-x^2+4\)
\(h(x)=x^2+3x-1\)
\(i(x)=x^5-6x^4-x\)
\(j(x)=x^7-4x^6-3x+7\)
\(k(x)=(x-2)^2\)

Påstående	Jämn funktion	Udda funktion
\(f(x)=3x^3-x\)
\(g(x)=-x^2+4\)
\(h(x)=x^2+3x-1\)
\(i(x)=x^5-6x^4-x\)
\(j(x)=x^7-4x^6-3x+7\)
\(k(x)=(x-2)^2\)