Repetition: 4. Funktioner

Diskutera parvis vad följande begrepp har och göra med funktioner

Linje
Parabel
Riktingskoefficient
Funktionsvärde
Nollställe
Växande funktion
Avtagande funktion

Uppgifter

Svara utgående från grafen nedan på följande frågor.

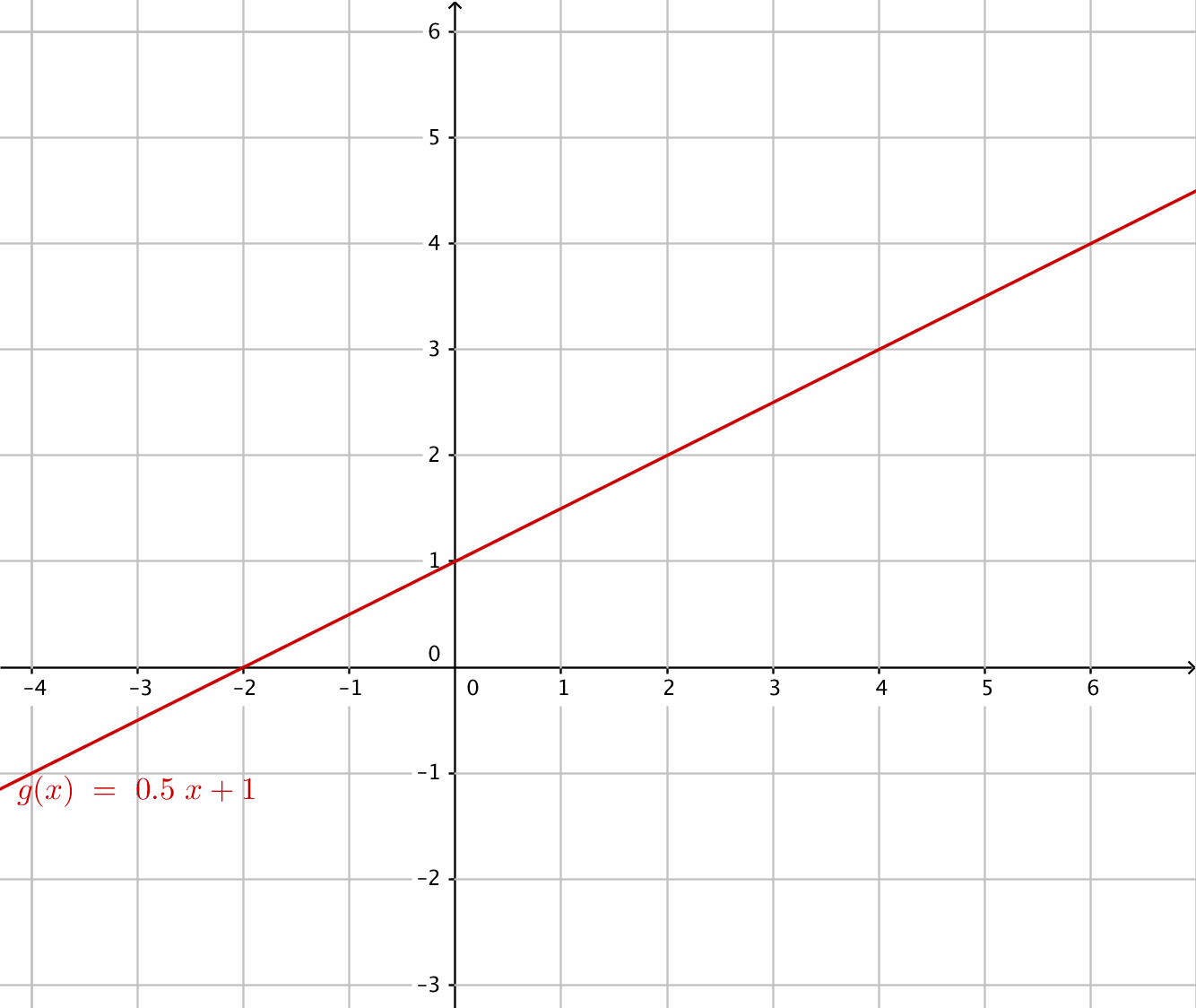
Bestäm
1. funktionsvärdet i punkten \(x=2\).
  
  Vi går till \( x = 2 \). Sedan tittar vi uppåt och nedåt och söker funktionen. Från funktionen går vi mot \(y\)-axeln. Funktionsvärde är 2.
2. Funktionsvärdet i punkten 4 är 3.
  
  Funktionsvärdet i punkten 4 är 3.
3. nollstället för funktionen.
  
  Vi söker de punkter som funktionen skär \(x\)-axeln, i dessa punkter har funktionen värdet noll. Nollstället är i punkten (-2,0).
Svara utgående från grafen nedan på följande frågor.

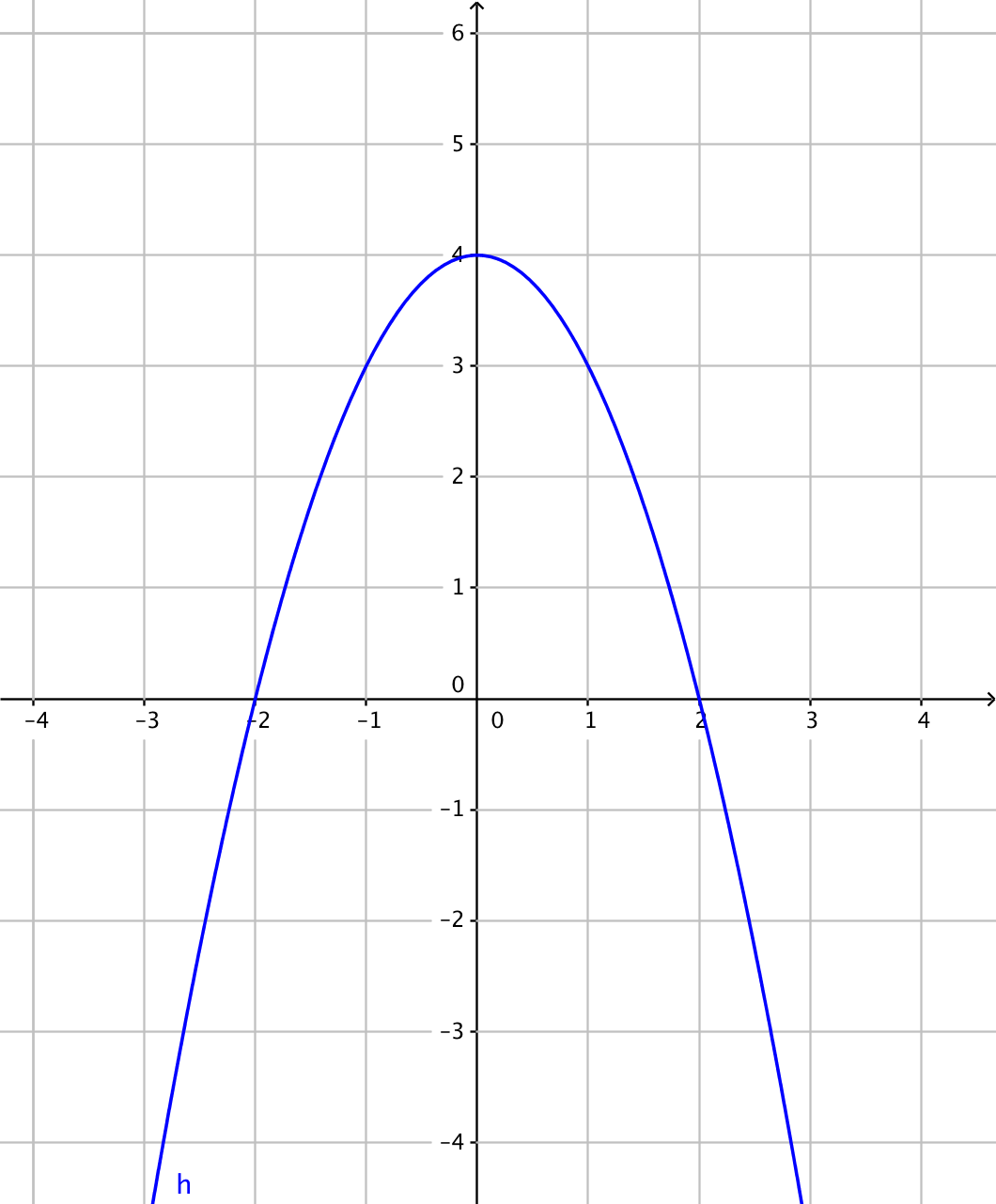
Bestäm
1. \(h(1)\)
  
  \(h(1)=3\)
2. \(h(x)=4\)
  
  Vi söker de punkter som ger funktionsvärdet 4. Alltså då \(x=0\).
3. nollställena
  
  Nollställena är i \(x=-2\) och i \(x=2\).
4. när funktionen är avtagande.
  
  Då \(x\geq 0\).

Välj rätt alternativ för funktionerna. Välj vid behov flera alternativ per påstående.

Påstående	Riktingskoefficenten har värdet -2.	Riktingskoefficenten har värdet -1.	Riktingskoefficenten har värdet 1.	Riktingskoefficenten har värdet 2.	Nollstället är \(x=0\).	Nollstället är \(x=1\).

Påstående	Riktingskoefficenten har värdet -2.	Riktingskoefficenten har värdet -1.	Riktingskoefficenten har värdet 1.	Riktingskoefficenten har värdet 2.	Nollstället är \(x=0\).	Nollstället är \(x=1\).

Använd dig av funktionen i bilden och svara på följande frågor.

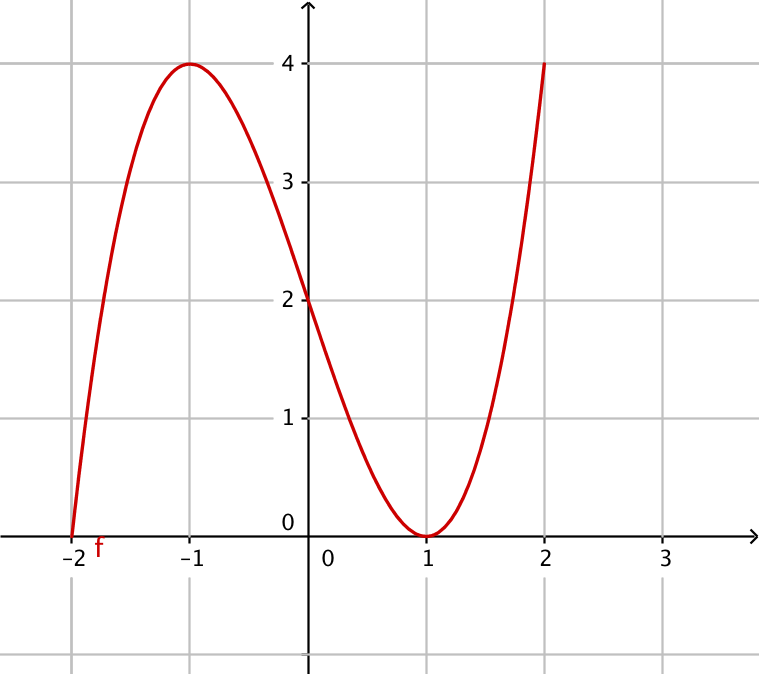
Bestäm när funktionen är
1. växande
  
  \(-2 \leq x \leq -1\) och \(1 \leq x \leq 2\)
2. avtagande
  
  \(-1 \leq x \leq 1\)
3. konstant?
  
  Då \(x=-1\) eller \(x=1\). Ur ett matematisk perspektiv kan vi kalla den konstant i dessa punkter.
4. Funktionens definitionsmängd.
  
  Funktionen är definierad då \( -2 \leq x \leq 2 \). (De tal som vi sätter in i funktionen).
5. Funktionens värdemängd?
  
  Funktionens värdemängd är \( 0 \leq y \leq 4 \). De värden som funktionen antar.
  
  Vi kan även skriva det som \( V_f \in [0,4] \).
Använd dig av funktionen i bilden och svara på följande frågor.

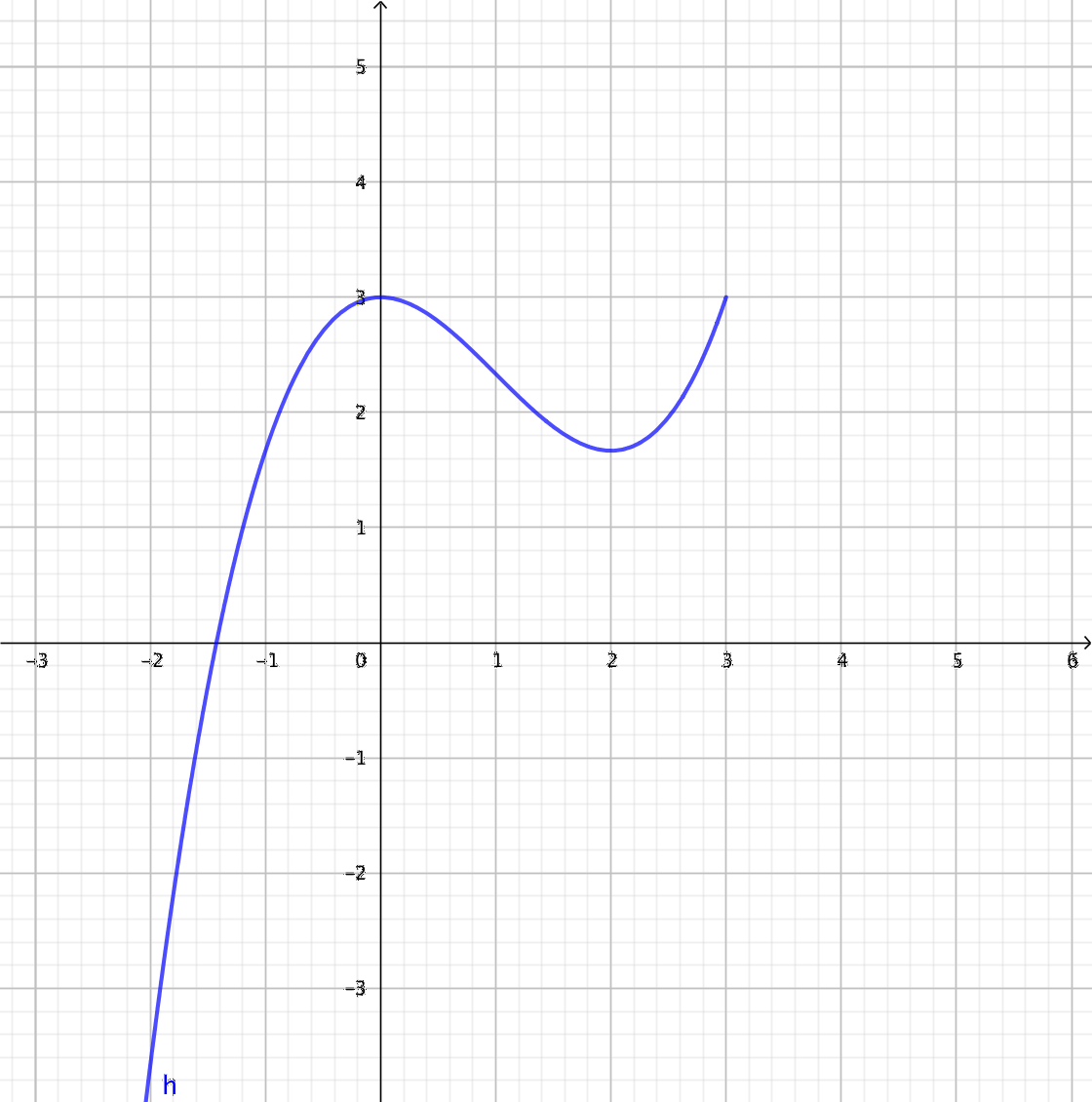
Bestäm när funktionen är
1. växande
  
  Från (minus) oändligheten fram till \( x = 0 \) och \(2 \leq x \leq 3\)
2. avtagande
  
  \(0 \leq x \leq 2\)
3. konstant?
  
  Då \(x=0\) eller \(x=2\). Ur ett matematisk perspektiv kan vi kalla den konstant i dessa punkter.
4. Funktionens definitionsmängd.
  
  Funktionen är definierad för tal som är mindre än 3.
5. Funktionens värdemängd?
  
  Funktionens värdemängd är alla reella tal mindre än 3.
  
  Vi kan även skriva det som \( V_h \in [-\infty,3] \).
Använd dig av funktionen i bilden och svara på följande frågor.

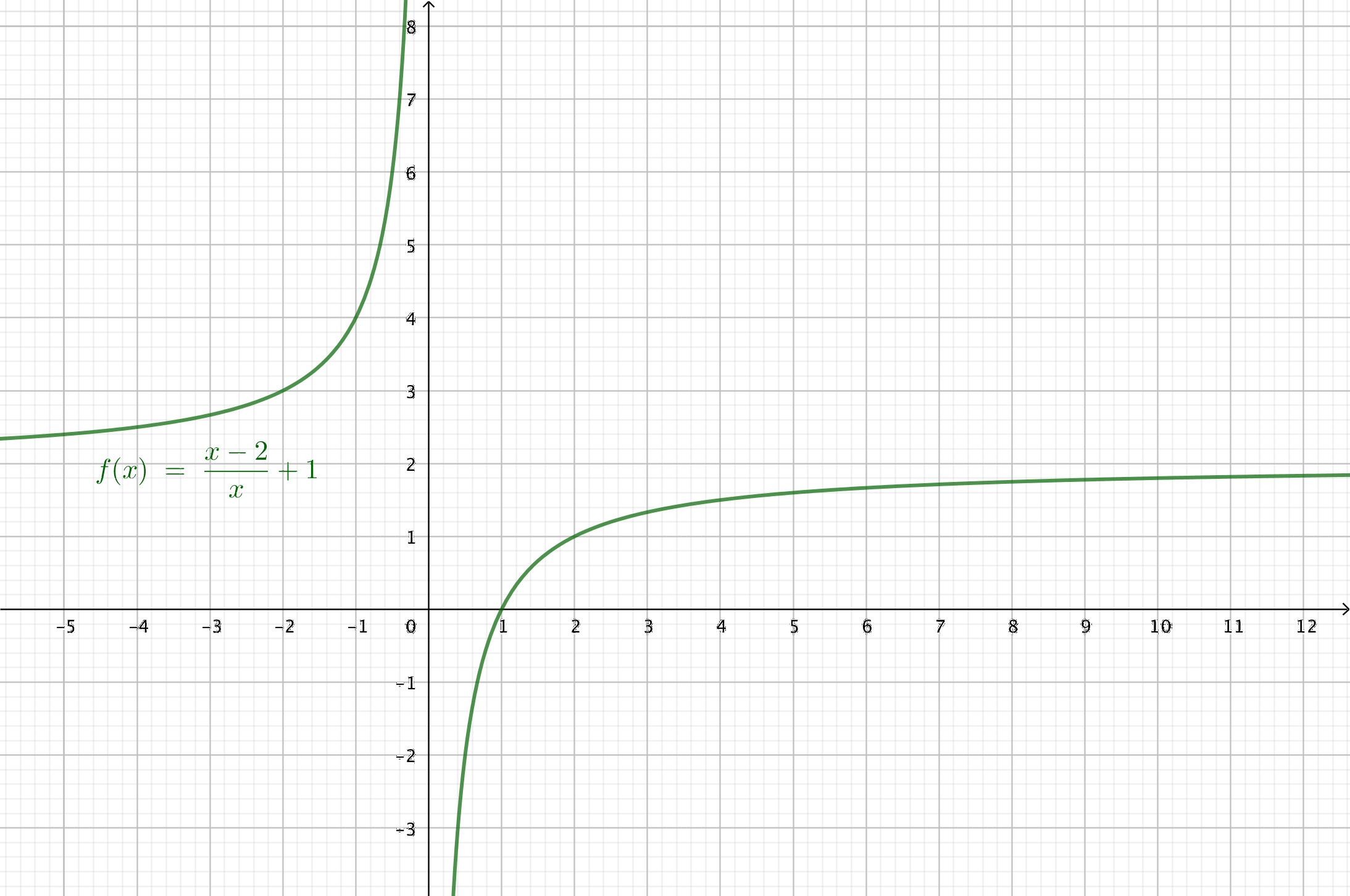
Bestäm när funktionen är
1. växande
  
  Funktionen är hela tiden växande. Vi kan även tala om att den är växande i sin värdemängd.
2. avtagande
  
  Den avtar aldrig.
3. konstant?
  
  Den är inte heller konstant.
4. Funktionens definitionsmängd.
  
  Funktionen är definierad i alla reella tal utom \( x = 0 \). Nämnarens nollställe.
5. Funktionens värdemängd?
  
  Funktionens värdemängd är alla reella tal.
6. Funktionens nollställen?
  
  Funktionens nollställe är \( x = 1 \).
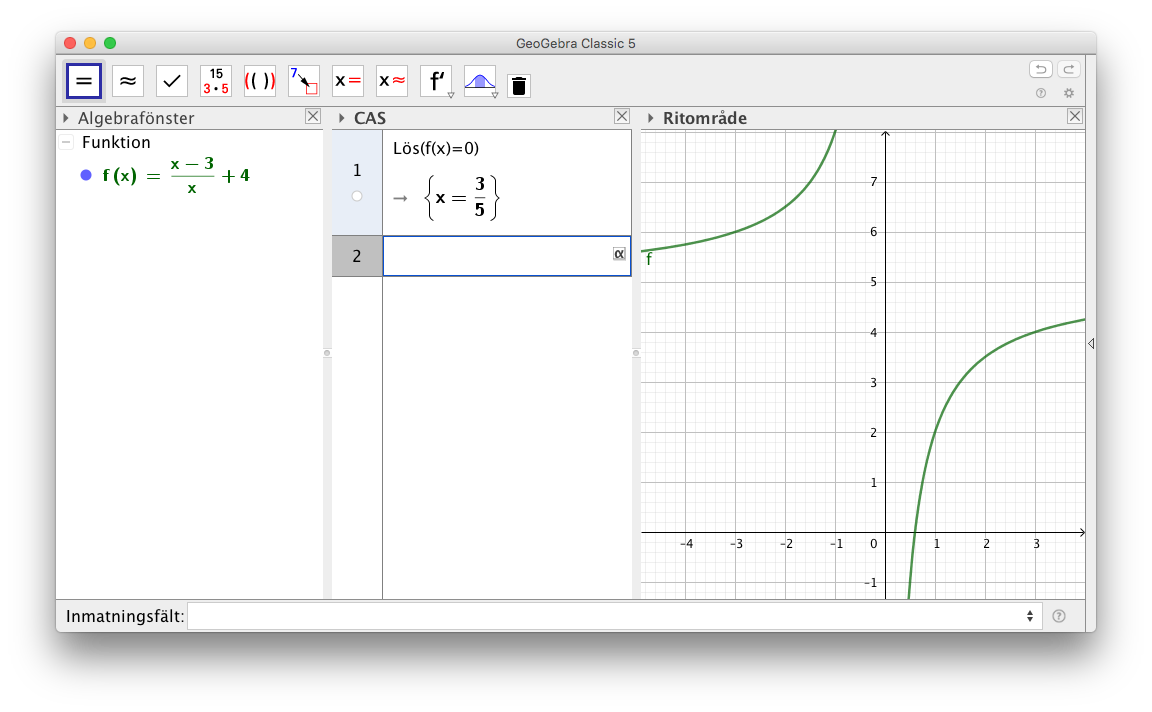
Lös nollstället för funktionen \( f(x)=\dfrac{x-3}{x} +4 \). Kontrollera din lösning genom att rita upp funktionen på tex GeoGebra (eller motsvarande) och lös nollstället mha räknarprogram.

Nollstället är den punkt där funktionen får värdet noll. Vi har en nämnare med ett \( x \), nämnaren får inte få värdet noll. Funktionen är inte definierad i \( x = 0 \).

Nollstället

\( \begin{array}{rcl} \dfrac{x-3}{x}+ 4 & = & 0 \\ \dfrac{x-3}{x} & = & -4 \\ \dfrac{x-3}{x} & = & -4 \\ x-3 & = & -4x \\ x+4x & = & 3 \\ 5x & = & 3 \\ x & = & \dfrac{3}{5} \\ \end{array} \)

Då vi ritar funktioen på GeoGebra får vi. (Skriv in uttrycket i Inmatningsfält:)

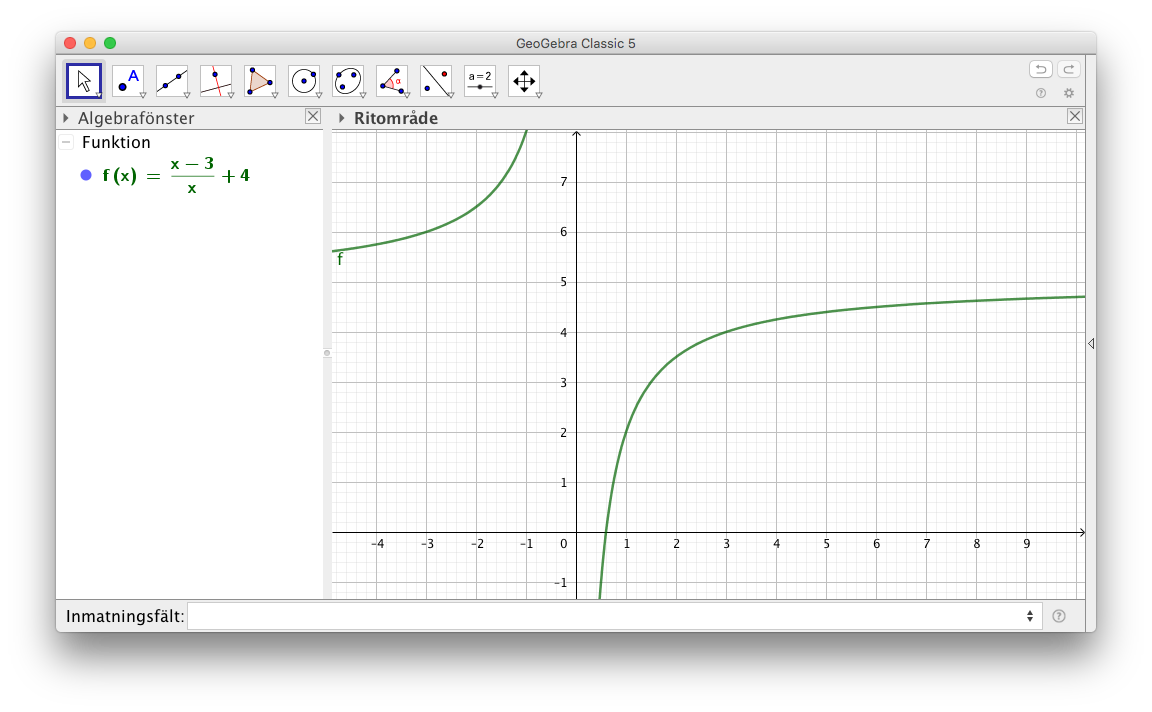
Ekvationen kan vi lösa i CAS.