Repetition: 3. Matematiskt tänkande och matematiska metoder

Uppgifter

1. Kombinera rätt geometrisk figur med rätt definition. Välj bland

   Fyrhörning

   Kvadrat

   Parallellogram

   Parallelltrapets

   Rektangel

   Romb

   Benämning	Påstående
   	Har fyra sidor.
   	Har fyra sidor där två sidor är parallella.
   	Har fyra sidor där motstående sidor är parallella.
   	Har fyra lika långa sidor.
   	Har fyra sidor där motstående sidor är parallella och vinklarna räta.
   	Har fyra lika långa sidor och räta vinklar.

   Lösning

   Benämning	Påstående
   Fyrhörning	Har fyra sidor.
   Parallelltrapets	Har fyra sidor där två sidor är parallella.
   Parallellogram	Har fyra sidor där motstående sidor är parallella.
   Romb	Har fyra lika långa sidor.
   Rektangel	Har fyra sidor där motstående sidor är parallella och vinklarna räta.
   Kvadrat	Har fyra lika långa sidor och räta vinklar.

2. Välj rätt alternativ för figuerna. Du kan kryssa i flera val för varje figur.

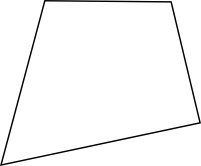
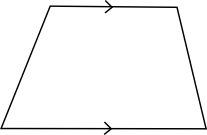
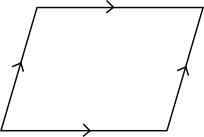
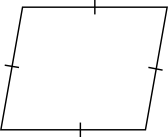
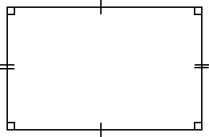
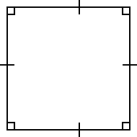
   Påstående	Fyrhörning	Kvadrat	Parallellogram	Parallelltrapets	Rektangel	Romb

   Lösning

   Påstående	Fyrhörning	Kvadrat	Parallellogram	Parallelltrapets	Rektangel	Romb

3. Lös följande ekvation, \( 4x - 9 = 2(x+5) \) och korrigera felen nedan.

   \( \begin{array}{rcl} 4x - 9 & = & 2(x+5) \\ 4x - 9 & = & 2x + 5 \\ 4x + 2x & = & 5 - 9 \\ 6x & = & -4 \\ x & = & -\dfrac{6}{4} = -\dfrac{3}{2} \\ \end{array} \)

   Lösning

   Den rätta lösningen är

   \( \begin{array}{rcl} 4x - 9 & = & 2(x+5) \\ 4x - 9 & = & 2x + 10 \\ 4x - 2x & = & 10 - 9 \\ 2x & = & 1 \\ x & = & \dfrac{1}{2} \\ \end{array} \)

   Felen är

   • Rad 2. \( 2 \cdot 5 = 10 \) är inte uträknat.
   • Rad 3. Termerna är inte de motsatta, \( +2x \) borde vara \( -2x \) och \( -9 \) borde vara 9.
   • Rad 5. Divisionen är fel. Det skall delas med talet framför \( x \). Det borde ha delats med 6.

4. Ordna uträkningarna i rätt ordning så att lösningen av ekvationen är logisk och korret.

   Välj bland följande uttryck

   \( 4x-4 = 3x+6 \)

   \( x = 10 \)

   \( 4x -3x = 6 +4 \)

   Uttryck	Ordningsföljd
   \( 4(x-1) = 3(x+2) \)	(1.)
   	(2.)
   	(3.)
   	(4.)

   Lösning

   Uttryck	Ordningsföljd
   \( 4(x-1) = 3(x+2) \)	(1.)
   \( 4x-4 = 3x+6 \)	(2.)
   \( 4x -3x = 6 +4 \)	(3.)
   \( x = 10 \)	(4.)

5. Ordna uträkningarna i rätt ordning så att lösningen av ekvationen är logisk och korret.

   Välj bland följande uttryck

   \( - 3x = 10 \)

   \( x-2 = 8+4x \)

   \( \dfrac{4(x-2)}{4} = 4(2+x) \)

   \( x = -\dfrac{10}{3} \)

   \( x - 4x = 8 +2 \)

   Uttryck	Ordningsföljd
   \( \dfrac{x-2}{4} = 2+x \)	(1.)
   	(2.)
   	(3.)
   	(4.)
   	(5.)
   	(6.)

   Lösning

   Uttryck	Ordningsföljd
   \( \dfrac{x-2}{4} = 2+x \)	(1.)
   \( \dfrac{4(x-2)}{4} = 4(2+x) \)	(2.)
   \( x-2 = 8+4x \)	(3.)
   \( x - 4x = 8 +2 \)	(4.)
   \( - 3x = 10 \)	(5.)
   \( x = -\dfrac{10}{3} \)	(6.)

6. Daniel tycker om att simma. När han simmar alternar han mellan bröst och crawl. Han simmar i en bassägn om 25 m och om han byter simstil så gör han det vid varje 25 m längd.

   Efter att han simmat ett tag konstaterar han följande: "Då jag har simmat 75 m har jag simmat 66 % av sträckan crawl och resten bröst. Efter 100 m har jag simmat 75 % av sträckan som cralw och resten bröst."

   Han simmar högst 50 m av en stil i ett sträck. Hur har han simmat?

   Lösning

   Det första påståendet ger oss att han har simmat 25 m bröst och 50 m crawl. Då kan han ha simmat:

   • crawl, bröst och crawl
   • crawl, crawl och bröst
   • bröst, crawl och crawl

   För att det andra skall gälla får vi :

   • crawl, bröst, crawl och crawl
   • crawl, crawl, bröst, crawl
   • bröst, crawl, crawl och crawl

   Alltså har han simmat: "crawl, bröst, crawl och crawl" eller "crawl, crawl, bröst, crawl"

7. Varför får man inte dividera med noll?

   Lösning

   Vi börjar med att se på \(\dfrac{12}{4} = 3 \), som betyder att \(3\cdot 4 = 12 \).

   Allmänt betyder det att \(\dfrac{a}{b}=c \Leftrightarrow c\cdot b =a \).

   Om vi tillåter \(b=0 \) får vi att

   \(1 \cdot 0 = \) något,

   \(2 \cdot 0 = \) något annat och

   \(3 \cdot 0 = \) något tredje.

   Men vi vet från tidigare att då vi multiplicerar med noll skall vi få svaret noll, tex \(2 \cdot 0 = 0 \) och \(3\cdot 0 =0 \).

   Då kan vi inte ha fall där vi inte vet vad noll gånger något är.

   Därför får vi inte dividera med noll.