13. Repetition
Som det sista för kursen är att repetera.
Uppgifter
- Kombinera rätt primitivfunktion med rätt funktion. Välj bland följande primitiva funktioner:
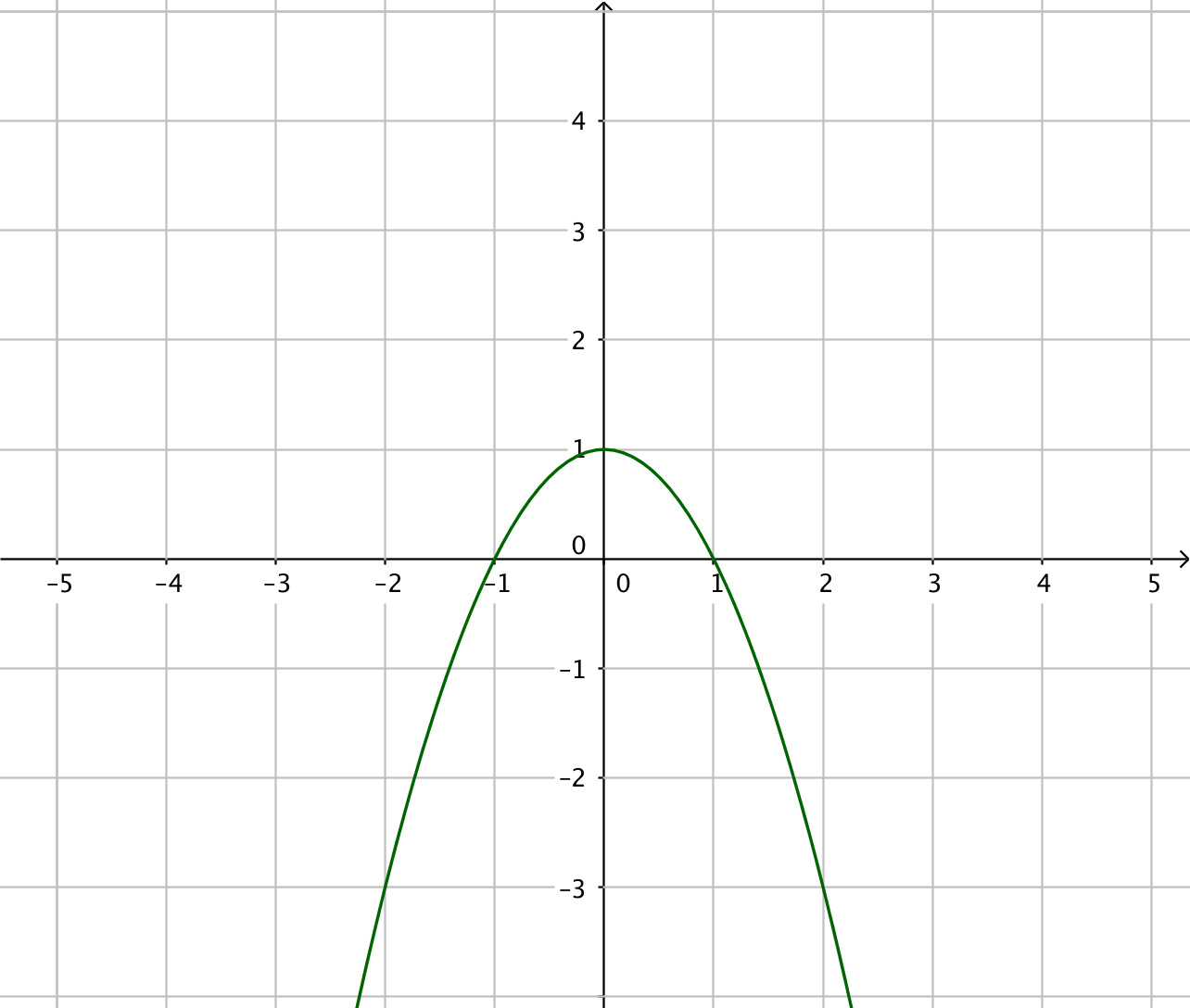
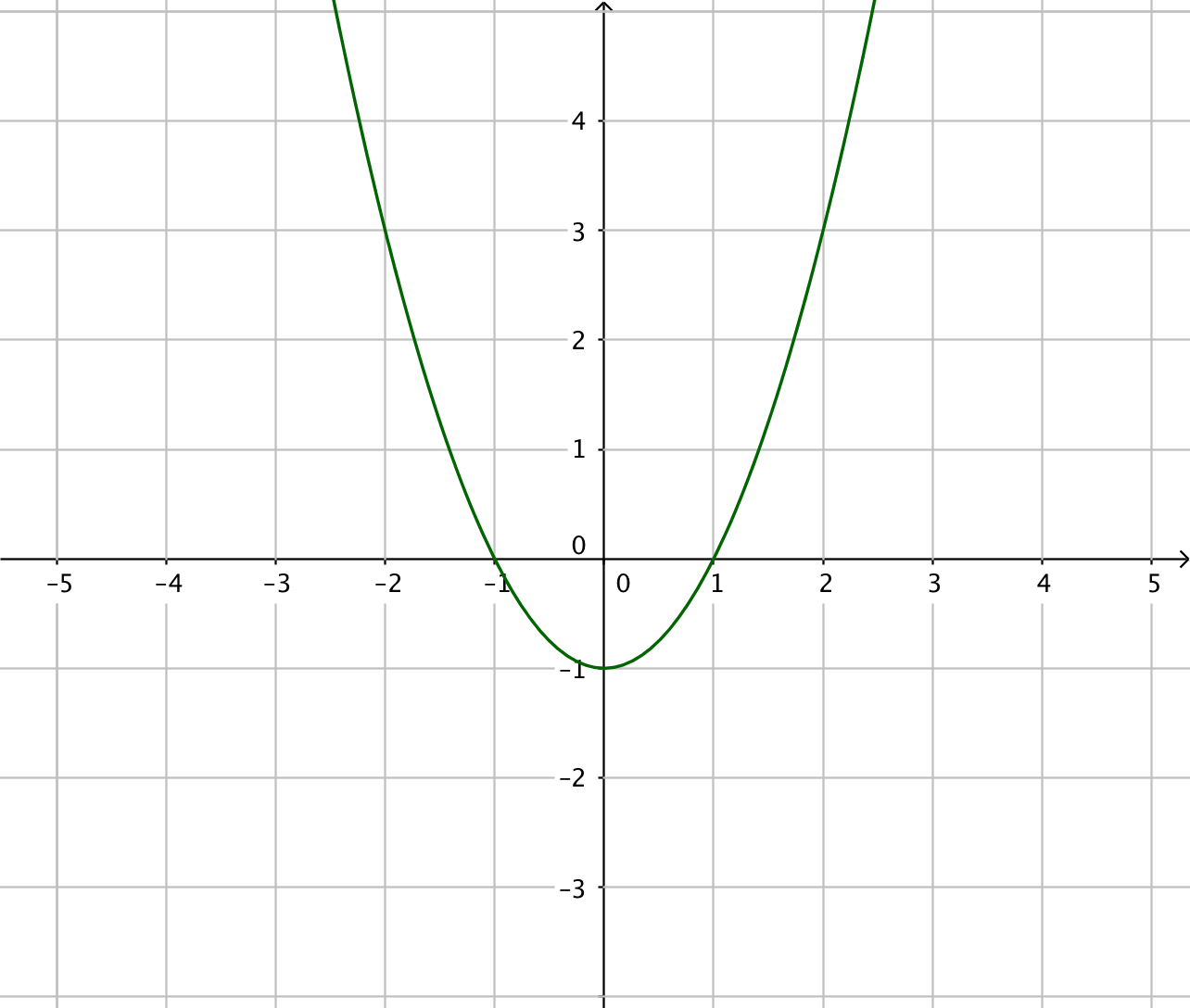
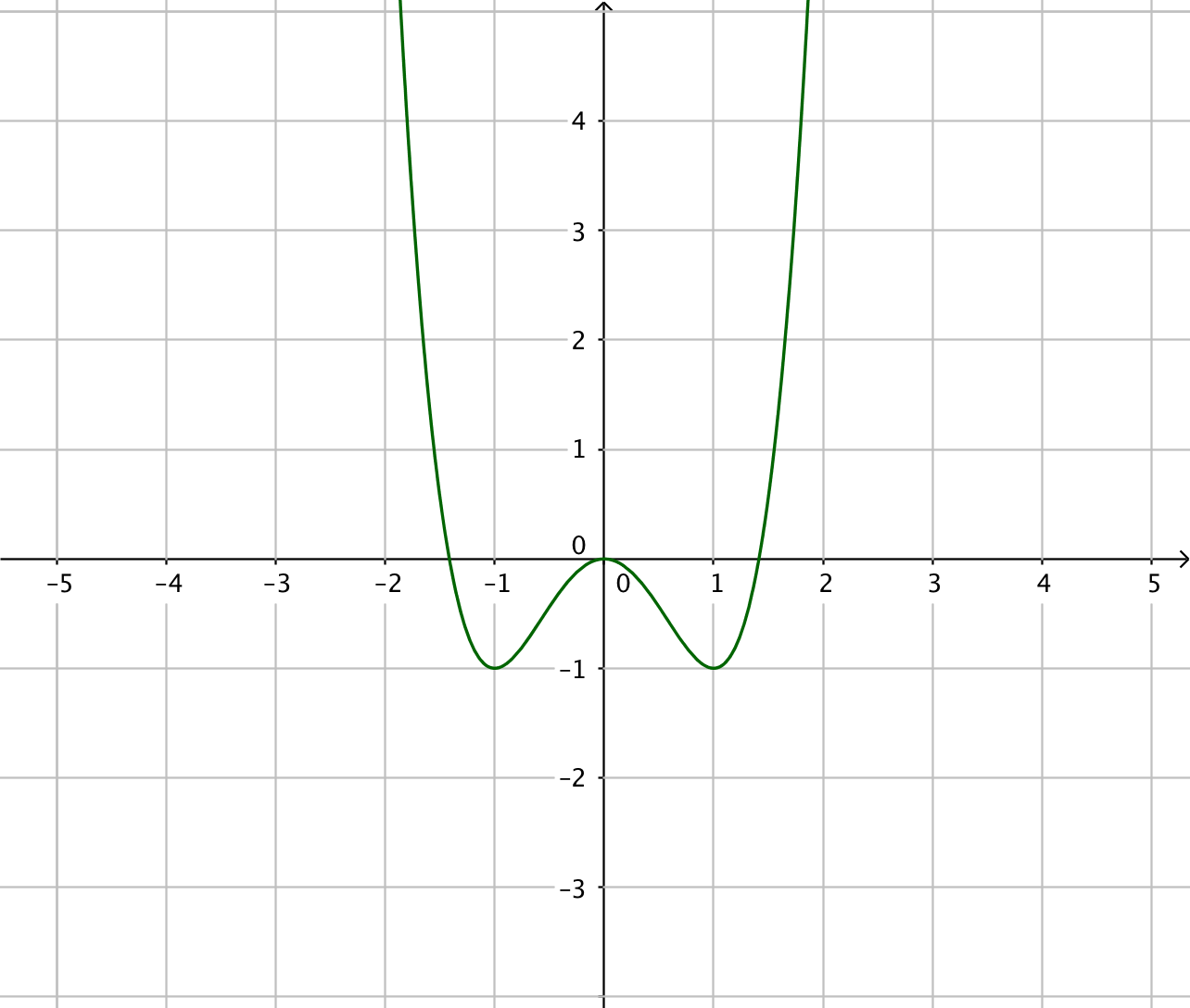
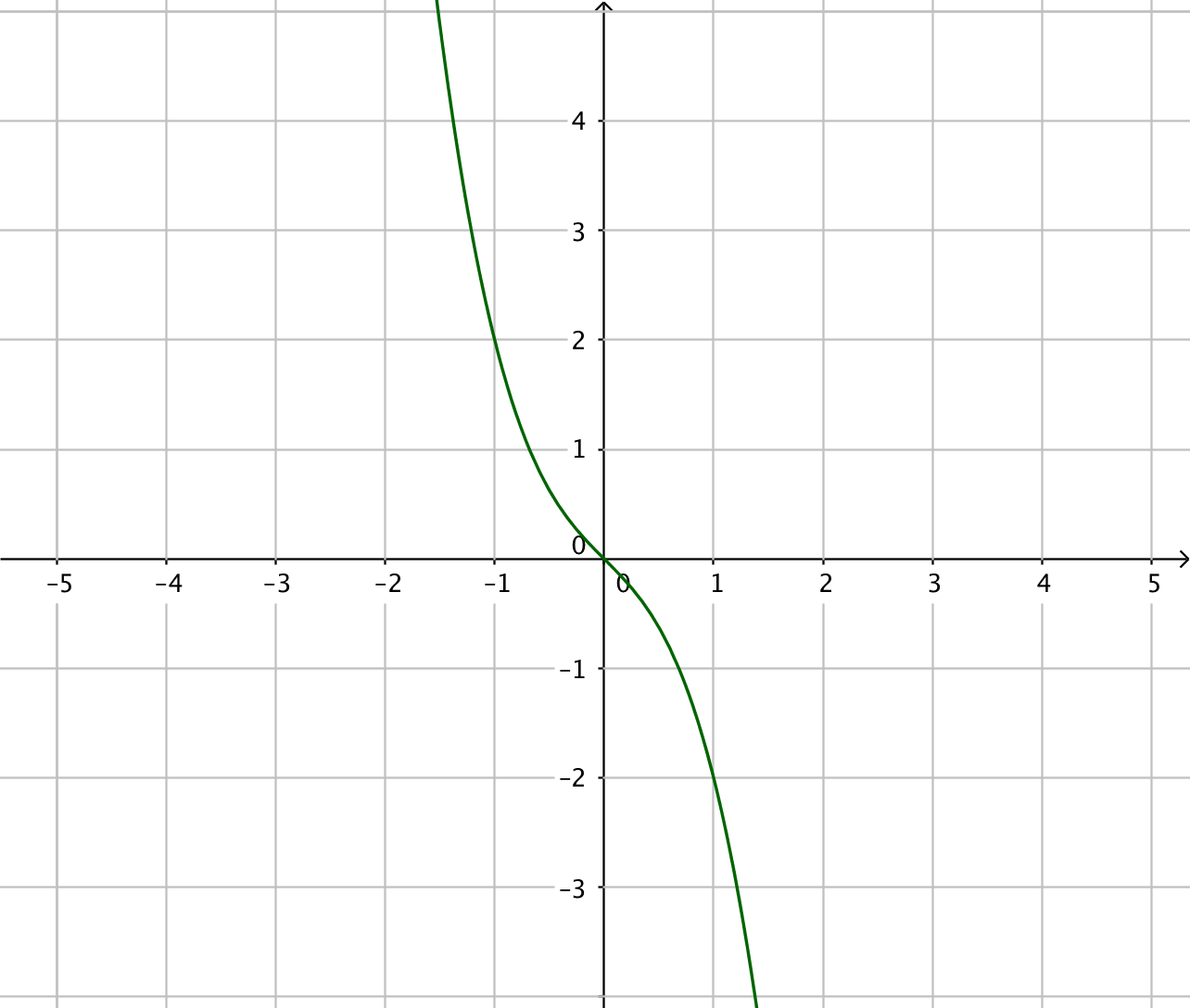
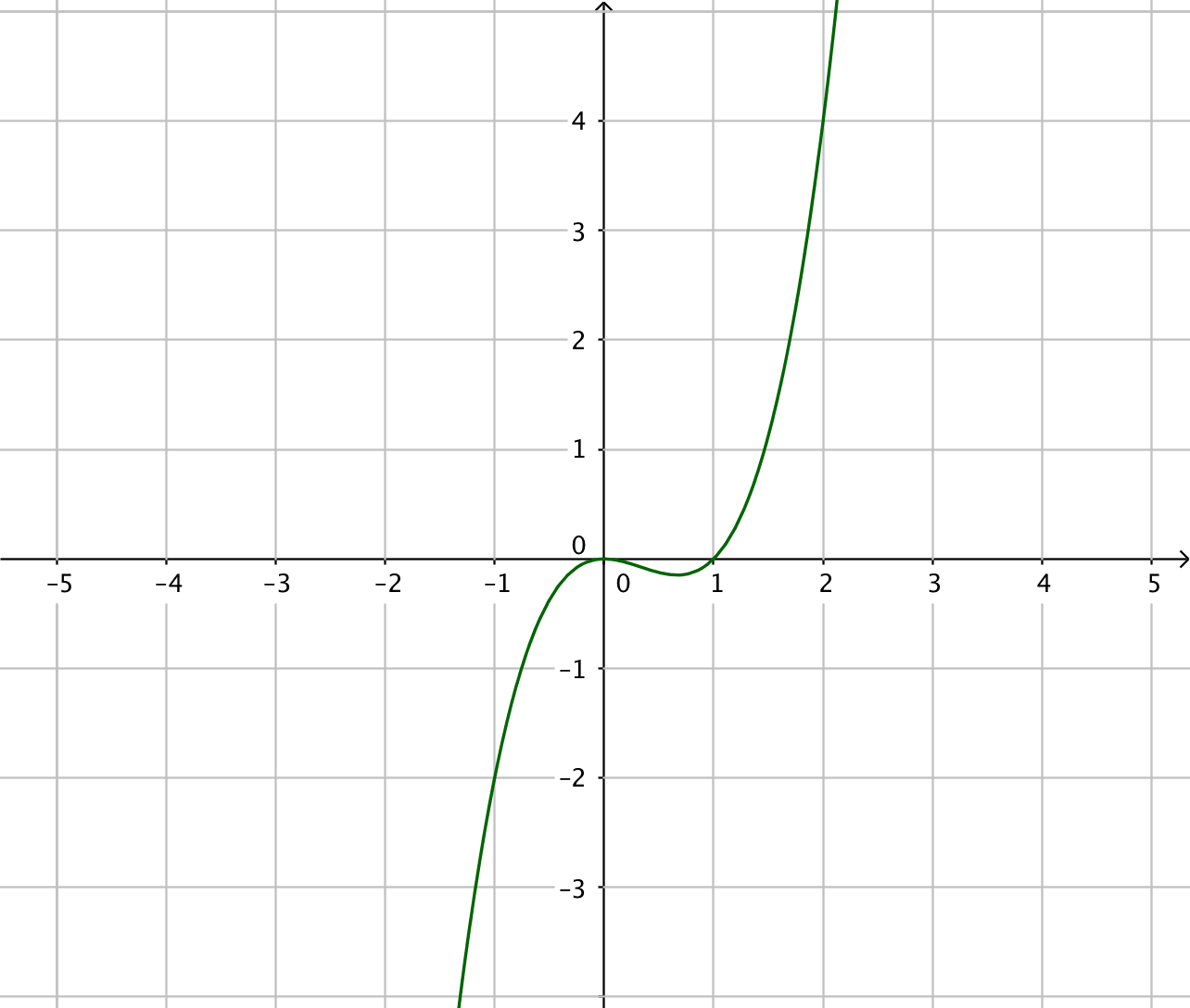
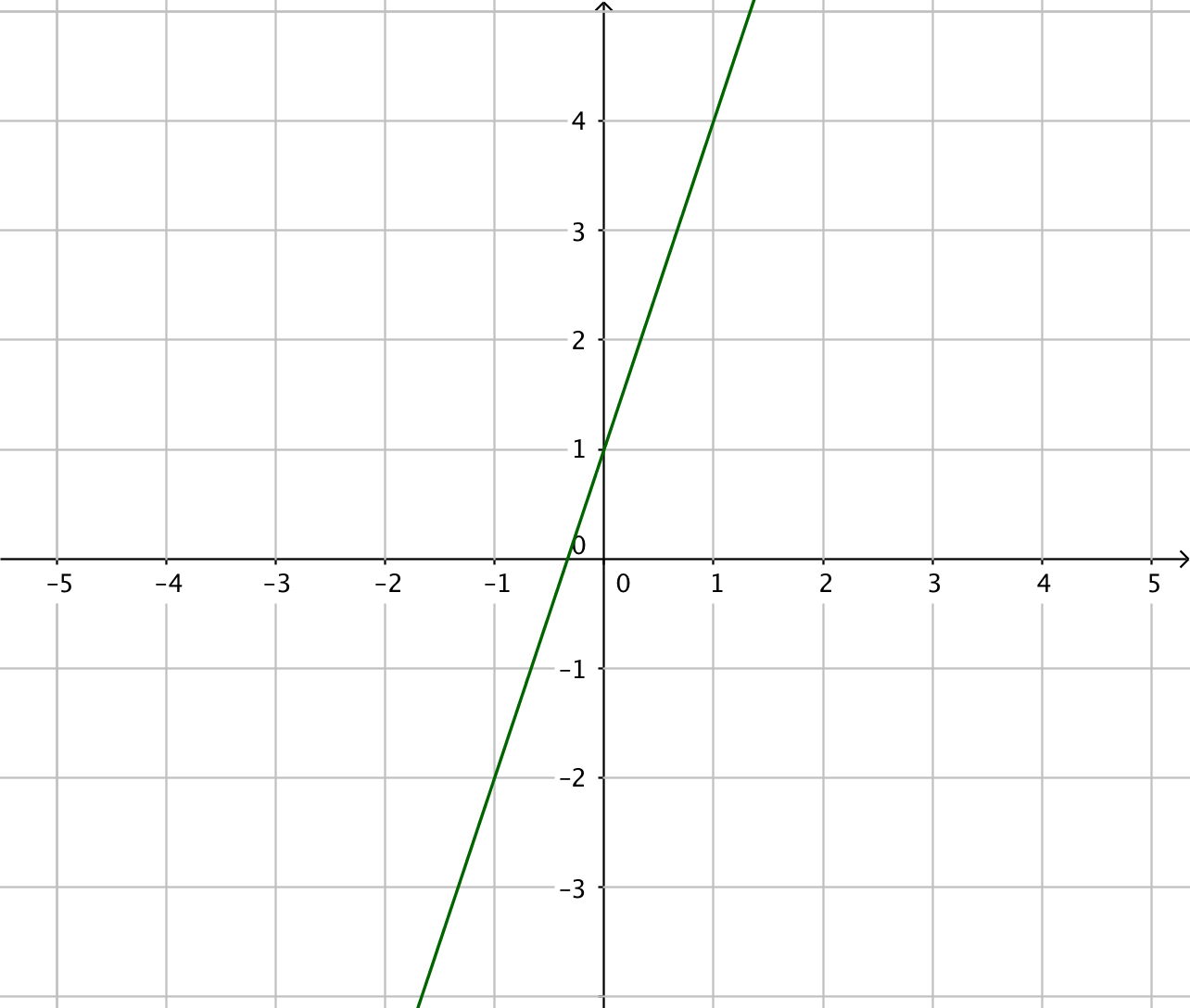
Primitiv funktion Funktion 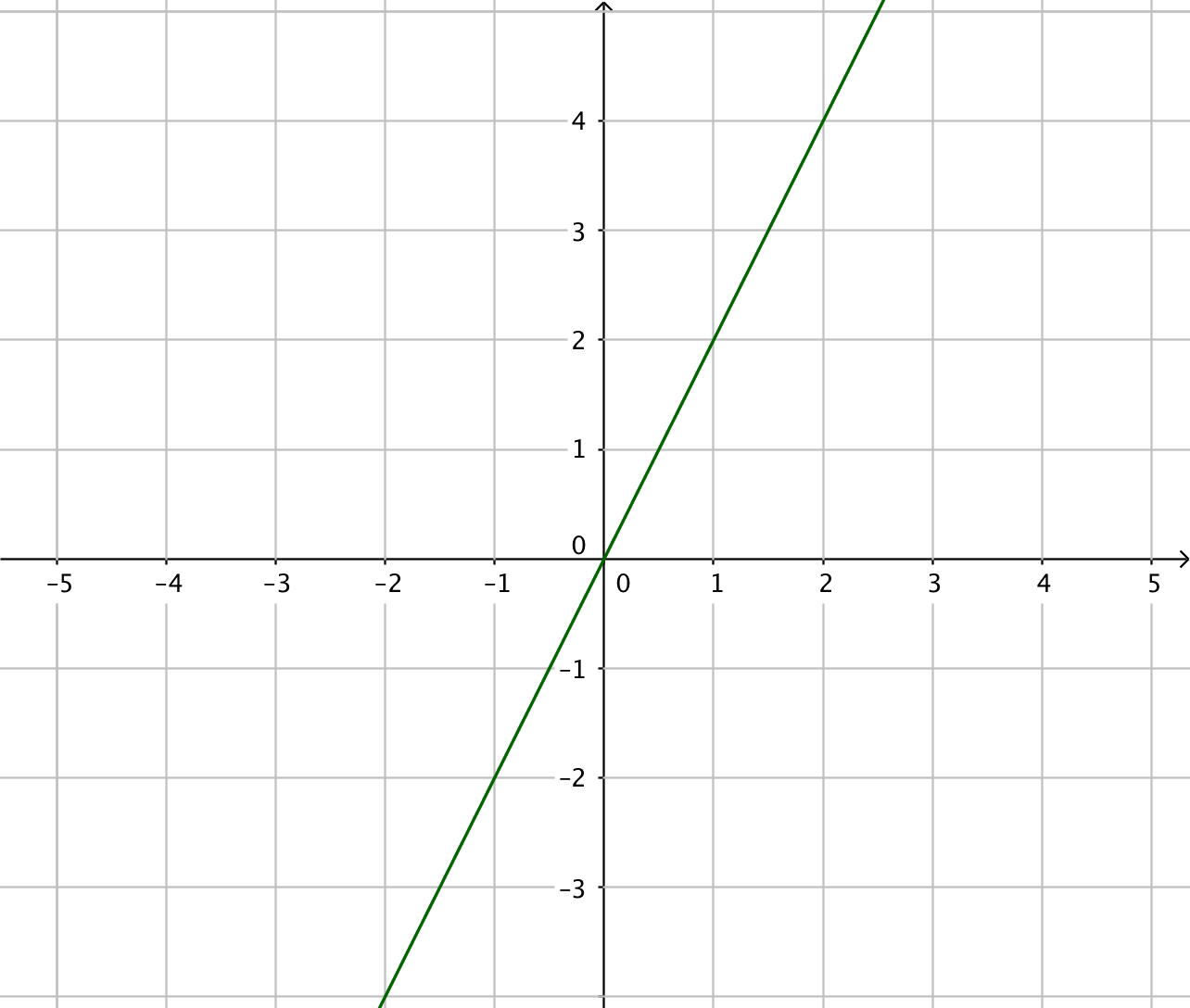
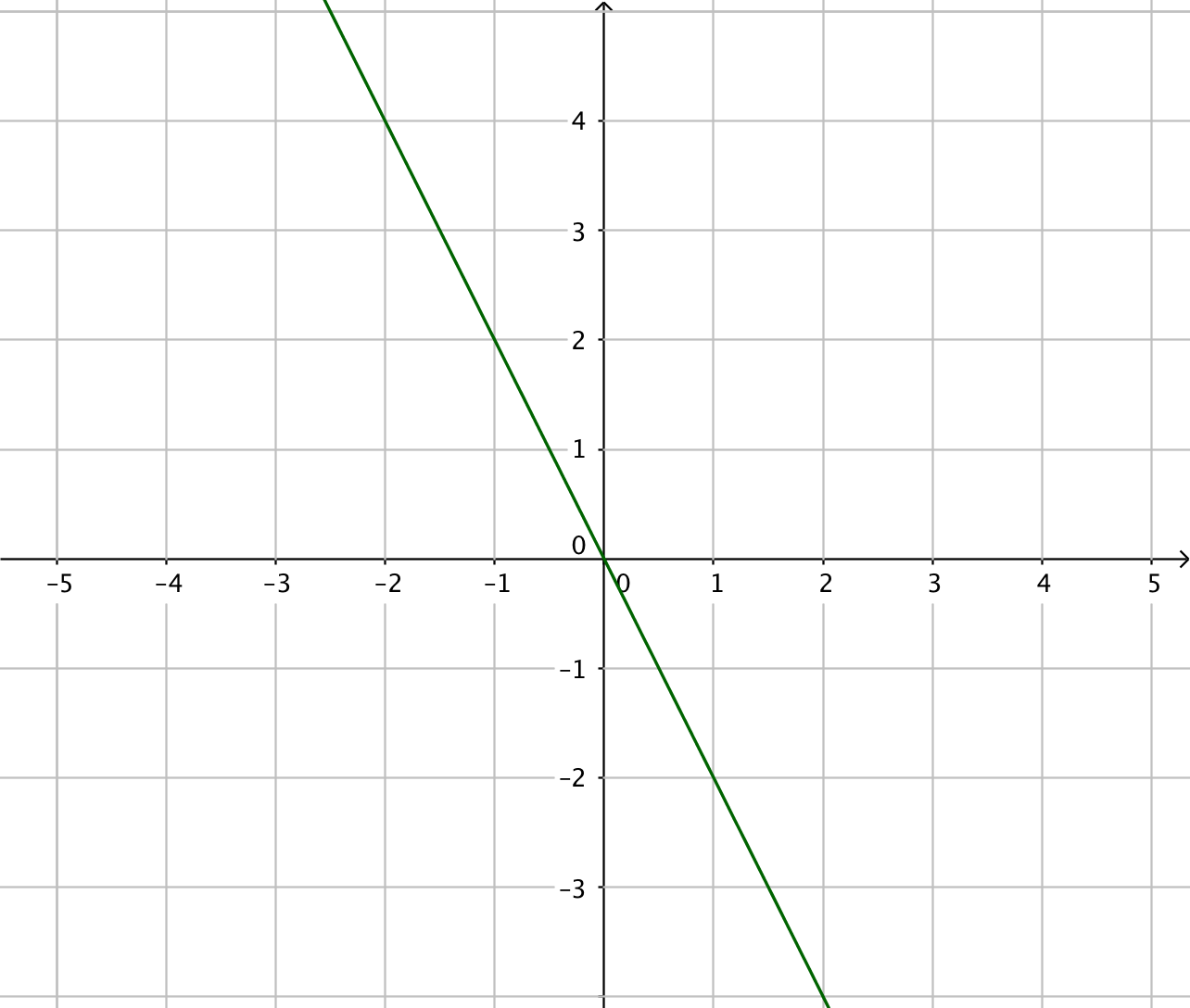
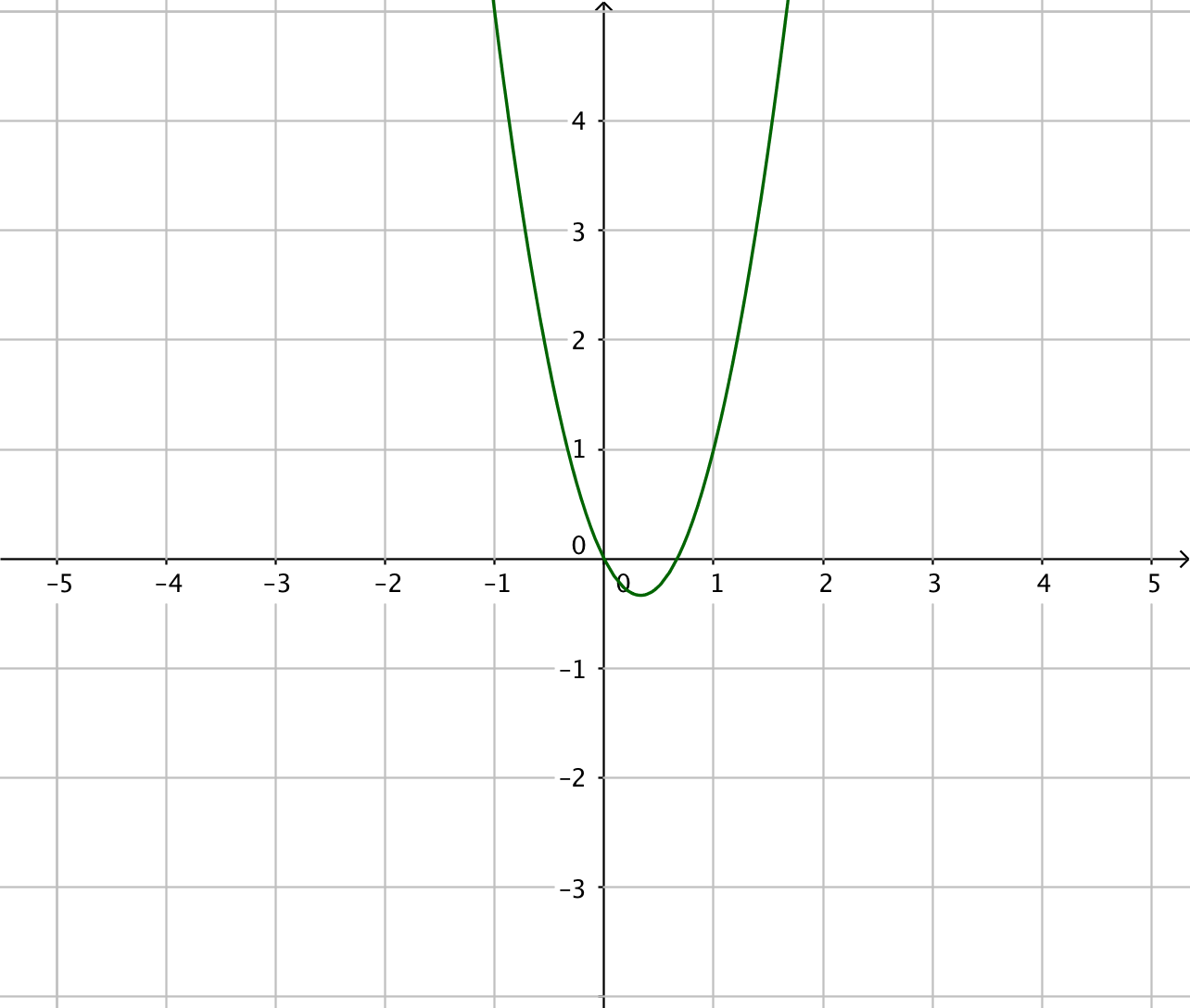
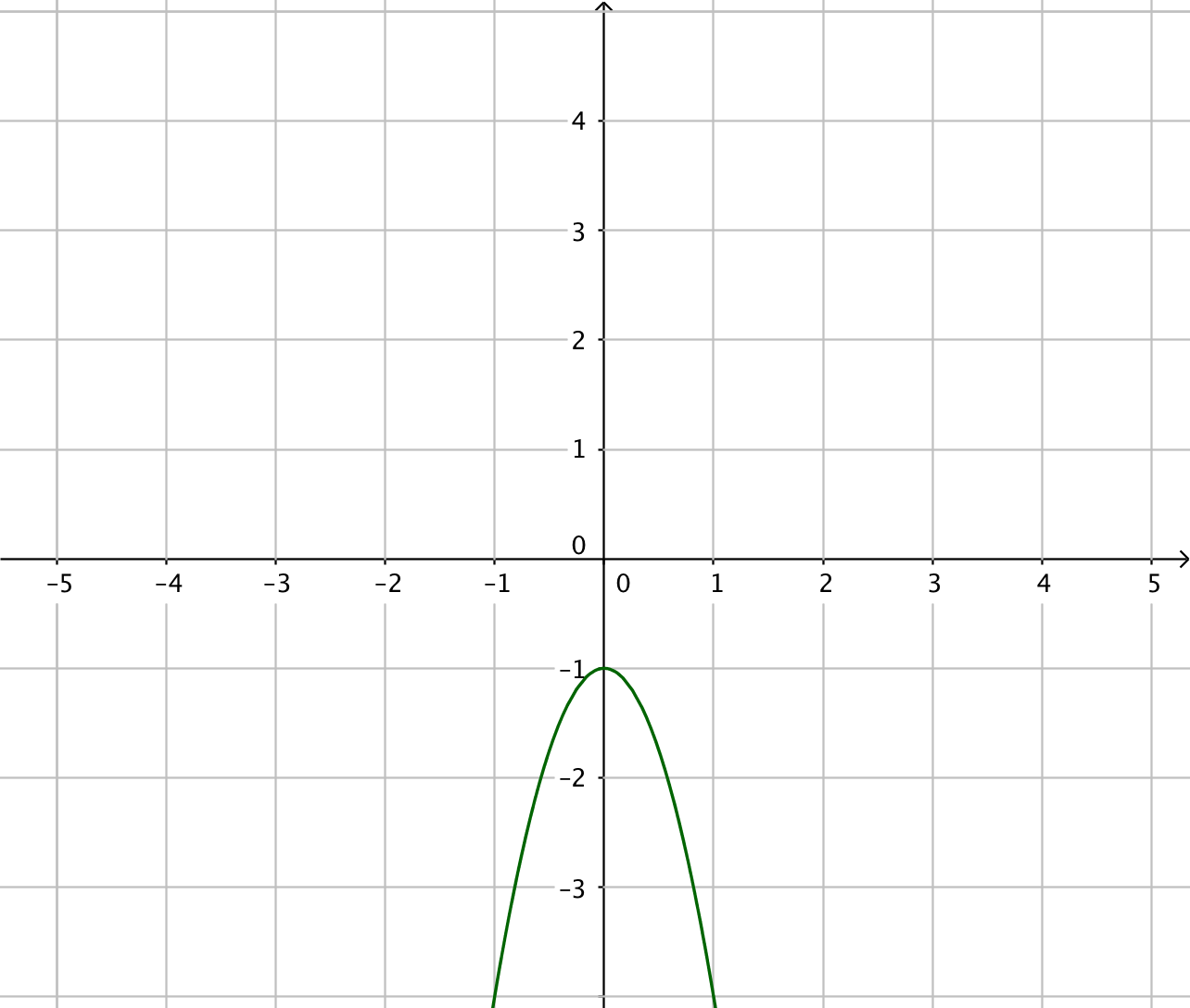
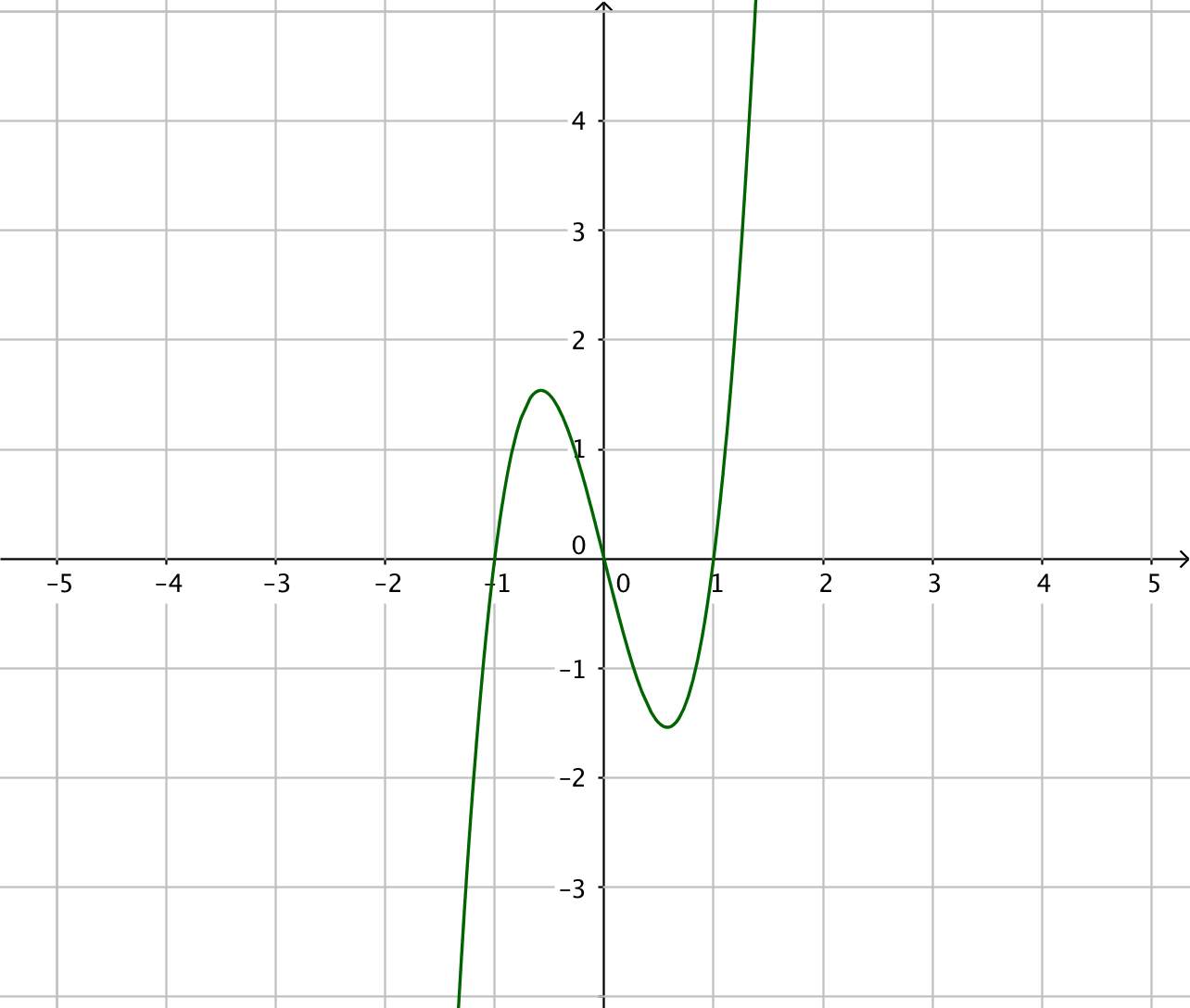
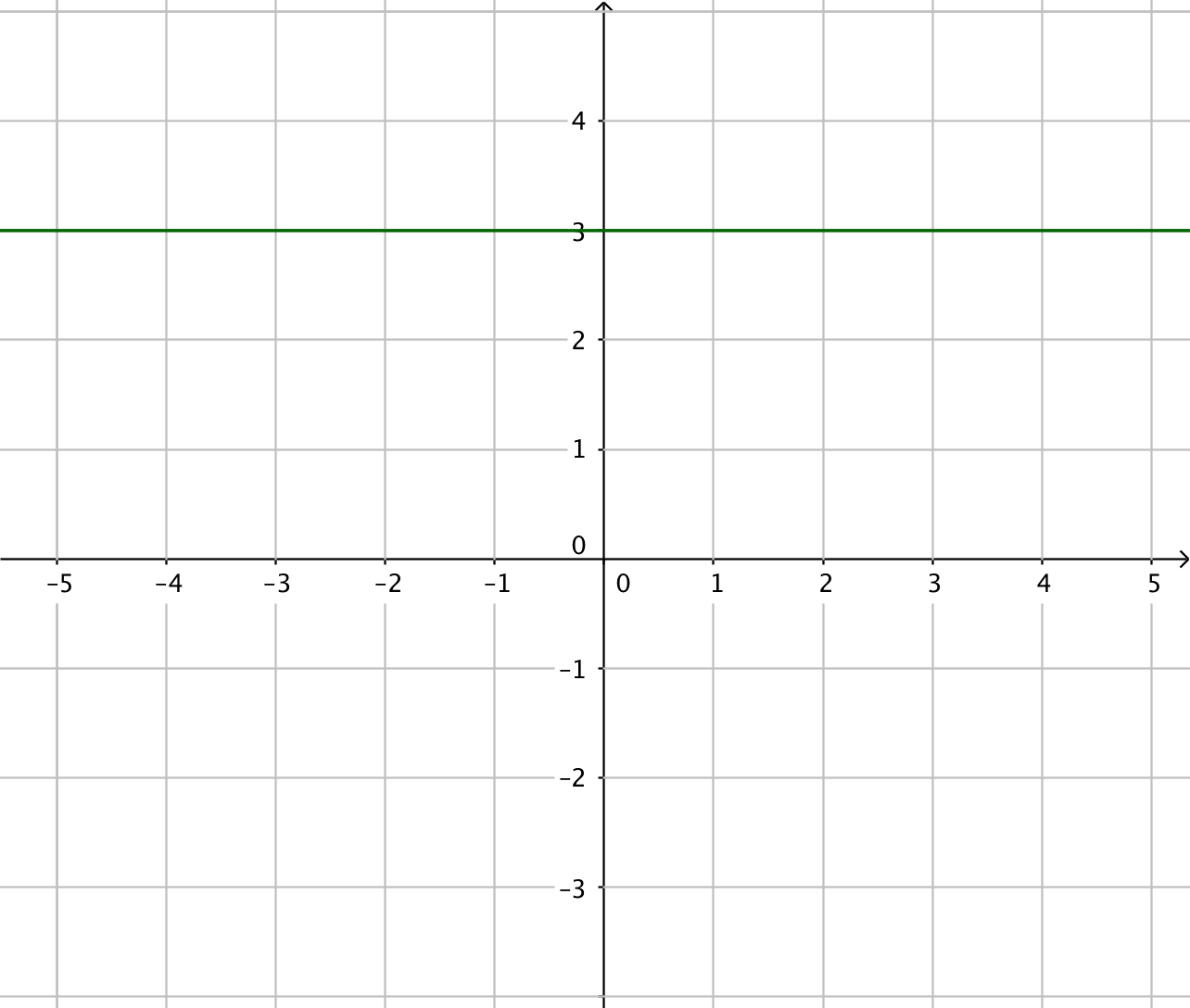
Tänk som så att du har derivatafunktionerna till höger. Vilken funktion har du deriverat för att komma till funktionen till höger? Arbeta med gradtalen, jämför dem! Vad händer med gradtalen då du deriverar?
Primitiv funktion Funktion 











- Bestäm den primitiva funktionen för följande uttryck.
Dessa är av sådan typ att du borde klara av att lösa dem utan räknare.
- \( 6x^2 - 4 \)
\( 2x^3-4x+C \)
- \( \dfrac{2}{3x} \)
\( \dfrac{2}{3} \ln \mid x \mid + C \)
- \( \cos 3x \)
\( \dfrac{1}{3}\sin(3x)+C \)
- \( e^{2x} \)
\( \dfrac{1}{2}e^{2x}+C \)
- \( x\cos x^2 \)
\( \dfrac{1}{2}\sin x^2 + C \)
- \( e^{4x-1} \)
\( \dfrac{1}{4}e^{4x-1} + C \)
- \( 6x^2 - 4 \)
- Bestäm följande integraler för hand. Kontrollera din lösning med CAS.
- \( \displaystyle\int (3e^{2x} + e^{-x}) \text{ d}x \)
Kom ihåg att ha den inre funktionens derivata framför!
\( \displaystyle\int (3e^{2x} + e^{-x}) \text{ d}x = \displaystyle\int (3\cdot\dfrac{1}{2}\cdot 2e^{2x} + (-1)(-1)e^{-x}) \text{ d}x = \dfrac{3}{2}e^{2x}-e^{-x} + C \).
- \( \displaystyle\int (\sin 2x -2 \cos\dfrac{x}{2}) \text{ d}x \)
Kom ihåg att ha den inre funktionens derivata framför!
\( \displaystyle\int (\sin 2x -2 \cos\dfrac{x}{2}) \text{ d}x = \displaystyle\int (\dfrac{1}{2}\cdot 2\sin 2x -2\cdot2\cdot\dfrac{1}{2}\cos\dfrac{x}{2}) \text{ d}x = \dfrac{1}{2}(-\cos 2x) -4\sin\dfrac{x}{2} + C \)
- \( \displaystyle\int (3e^{2x} + e^{-x}) \text{ d}x \)
- Bestäm de primitiva funktionerna så att de går genom en bestämd punkt.
- \( f(x) = 3x^2 + 5 \) så att den primitiva funktionen går genom \( (1,3) \).
\( F(x) = x^3 + 5x + C \).
Genom punkten \( (1,3) \) betyder att \( 1^3 +5\cdot 1 + C = 3 \), alltså \( C = -3 \). Alltså \( F(x) = x^3 + 5x + -3 \).
- \( f(x) = 12x^2 -14x \) så att den primitiva funktionen går genom \( (2,4) \).
\( F(x) = 4x^3 - 7x^2 + C \).
Genom punkten \( (2,4) \) betyder att \( 4\cdot 2^3 -7\cdot 2^2 + C = 4 \), alltså \( C = 0 \). Alltså \( F(x) = 4x^3 - 7x^2 \).
- \( f(x) = \cos (x) \) så att den primitiva funktionen går genom \( (\pi,1) \).
\( F(x) = \sin (x) + C \).
Genom punkten \( (\pi,1) \) betyder att \( \sin (\pi) + C = 1 \), alltså \( C = 1 \). Alltså \( F(x) = \sin (x) + 1 \).
- \( f(x) = 3x^2 + 5 \) så att den primitiva funktionen går genom \( (1,3) \).
- Bestäm den primitiva funktionen för \( f(x) = \dfrac{1}{x^3}-\dfrac{9}{x} \), där \( x > 0 \) och vars största värde är 0.
Den primitiva funktionen är \( F(x) = -\dfrac{1}{2x^2} - 9\ln x +C \).
För nollstället gäller att \( f(x) = 0\). Alltså \( \pm\dfrac{1}{3} \). Eftersom \( x > 0 \) har vi \( x = \dfrac{1}{3} \).
\( F(x) \) skall genom punkten \( (\dfrac{1}{3},0) \).
Vi får att \( F(x) = -\dfrac{1}{2x^2} - 9\ln x +\dfrac{9}{2} -9\ln 3 \).
- Bestäm storleken av arean som bildas mellan \( f(x)=-x^2+3x \) och \( x \)-axeln i intervallet \( [0,2] \).
\( \displaystyle\int_0^2 -x^2+3x \mathrm{ d}x = \bigg/_0^2 -\dfrac{1}{3}x^3+3\dfrac{1}{2}x^2 = (-\dfrac{1}{3}\cdot 2^3+3\dfrac{1}{2}\cdot 2^2)-(-\dfrac{1}{3}\cdot 0^3+3\dfrac{1}{2}\cdot 0^2) = 3\dfrac{1}{3} \).
- Bestäm storleken av arean som bildas mellan \( f(x)=\dfrac{2}{x} \) och \( x \)-axeln i intervallet \( [1,4] \).
\( \displaystyle\int_1^4 \dfrac{2}{x} \mathrm{ d} x = \bigg/_1^4 2\ln x = 2(\ln 4- \ln 1) = 2\ln 4 = 2\ln 2^2 = 4 \ln 2 \).
- Bestäm storleken av arean som bildas mellan \( f(x)=\sin \dfrac{x}{2} \) och \( x \)-axeln i intervallet \( [0,\pi] \).
\( \displaystyle\int_0^{\pi} \sin\dfrac{x}{2} \mathrm{ d}x = 2\displaystyle\int_0^{\pi} \dfrac{1}{2}\sin\dfrac{x}{2} \mathrm{ d}x =2 \bigg/_0^{\pi} -\cos \dfrac{x}{2} = -2(\cos \dfrac{\pi}{2}-\cos \dfrac{0}{2}) =-2(0-1) = 2 \).
- För vilket värde på \( a \) gäller att arean som bildas mellan \( f(x)=\dfrac{1}{2}x+1 \) och \( x \)-axeln i intervallet \( [1,a] \), \( a > 1 \), får värdet 4?
Vi får ekvationen \( \displaystyle\int_1^a \dfrac{1}{2}x+1 \mathrm{ d} x = 4 \) som har lösningen \( a=3 \).
- Bestäm storleken av arean som bildas mellan \( f(x)=x^2-2x+1 \) och \( g(x)=x+1 \).
Skärningspunkterna \( x^2-2x+1 = x+1 \) är 0 och 3.
Arean är \( \displaystyle\int_0^3 x+1-(x^2-2x+1)\mathrm{ d}x = \displaystyle\int_0^3 -x^2+3x \mathrm{ d} x = \bigg/_0^3 -\dfrac{1}{3}x^3+\dfrac{3}{2}x^2 = 4,5 \).
- Bestäm storleken av arean som bildas mellan \( f(x)=x^2+4x \) och \( g(x)=2x+3 \).
Skärningspunkterna är \( x^2+4x=2x+3 \Leftrightarrow x=-3 \) och \( x=1 \).
Arean är \( \displaystyle\int_{-3}^1 2x+3-(x^2+4x) \mathrm{ d} x =\displaystyle\int_{-3}^1 -x^2 -2x+3 \mathrm{ d} x = \bigg/_{-3}^1 -\dfrac{1}{3}x^3-x^2+3x = 10\dfrac{2}{3} \).
- Bestäm storleken av det ändliga området som bildas mellan koordinataxlarna och kurvorna \( y = 2 \ln x \) och \( y = 2 \).
Rita upp funktionerna på dator och konstatera att du behöver den inversa funktionen för \( y = 2 \ln x \).
Den inversa funktionen är \( x = e^{\frac{y}{2}} \), alltså \( f^{-1}(x)= e^{\frac{y}{2}} \).
Gränserna för integreringen är \( x=0 \) och \( x=2 \). Försäkra dig över dessa gränser!
Arean är \( \displaystyle\int_0^2 e^{\frac{y}{2}} \text{ d}x = 2e-2 \) a.e.
- För vilket värde på \( a \) gäller att arean som bildas mellan funktionen \( f(x) = \dfrac{1}{3x+a} \), \( x \)-axeln och linjerna \( x = 0 \) och \( x = 1 \) har storleken \( \ln 2 \)?
Vi får ekvationen \( \displaystyle\int_0^1 \dfrac{1}{3x+a} \text{ d}x = \ln 2 \).
Se till att du kan lösa ekvationen för hand, och på dator. Du har en sammansatt funktion!
Vi får \( \dfrac{1}{3} \bigg/_0^1 \ln (3x+a) = \ln 2 \). Kom ihåg att \( 3 \ln 2 = \ln 2^3 \).
Sätt in gränserna och få \( a = \dfrac{3}{7} \).
- Funktionen \( f(x) = 3x^2 +ax \) har en primitiv funktion vars nollställen är -2 och 1. Bestäm värdet för konstanten \( a \) och den primitiva funktionen för \( f \).
\( a = 6 \), den primitiva funktionen är \( F(x) = x^3+3x^2-4 \).
Den primitiva funktionen för \( f \) är av typ \( F(x) = x^3+\dfrac{1}{2}ax^2 +C \).
Från villkoret \( F(-2) = 0 \) och \( F(1) = 0 \) får vi ekvationerna \( -8+2a+C =0 \) och \( 1 + \dfrac{1}{2}a+C =0 \). Vi får \( a = 6 \) och \( C = -4 \).
- Funktionen \( f(x)=3x^2+1 \) då \( 0\leq x \leq 1 \) roterar kring \( x \)-axeln. Bestäm storleken av volymen som bildas för kroppen.
Volymen är \( \pi \displaystyle\int_0^1 (3x^2+1)^2 \mathrm{ d} x = \pi\displaystyle\int_0^1 9x^4+6x^2+1 \mathrm{ d} x = \pi \bigg/_0^1 \dfrac{9}{5}x^5 + 2x^3+x = \dfrac{24\pi}{5} \).
- För en polynomfunktion av tredje grad vet vi att derivatafunktionen har endast ett nollställe. Nollstället är i 2. Om funktionen \( f \) vet vi dessutom att \( f(1) = 0 \) och att \( f''(0) = 4 \). Bestäm funktionsvärdet \( f(-1) \).
Funktionsvärdet \( f(-1) = 8\dfrac{2}{3} \).
Vi vet att \( f'(x) = a(x-2)^2\), alltså \( f''(x) = 2a(x-2) \) och att \( f(x) = \dfrac{1}{3}a(x-2)^3+C \).
Villkoret \( f''(0) = 4 \) ger oss att \( a = -1 \) och villkoret \( f(1) = 0 \) ger oss att \( C=-\dfrac{1}{3} \).
Alltså är \( f(x) = -\dfrac{1}{3}(x-2)^3 -\dfrac{1}{3} \).
- Funktionen av \( f(x)=\cos x+2 \) roterar kring \( y=1 \) då \( x=\in [-\pi,\pi] \). Bestäm volymen av den kropp som uppstår.
Vi flyttar \( f \) neråt så att rotationen sker runt \( x \)-axeln. Den funktion som vi arbetar med är \( \cos x +2 -1 = \cos x +1 \).
Volymen är \( \pi \displaystyle\int_{-\pi}^{\pi} (\cos x +1)^2 =3\pi^2 \).
- Området mellan kurvan \( y = \dfrac{1}{x} \) och linjerna \( y = 2 \) och \( x = 2 \) roterar kring linjen \( y = 2 \). Bestäm volymen av kroppen som uppstår.
Kurvan \( y = \dfrac{1}{x} \) skär linjen \( y = 2 \) i \( x = \dfrac{1}{2} \).
Då kurvan roterar kring linjen \( y = 2 \) har tvärsnittsareorna värdet \( \pi (2-\dfrac{1}{x})^2 \) vid variablen \( x \).
Volymen för kroppen är \( V = \pi \displaystyle\int_{\frac{1}{2}}^2 (2-\dfrac{1}{x})^2 \text{ d}x = \pi(\dfrac{15}{2}-8\ln2) \approx 6,14 \).
Se till att du kan integera för hand och med hjälp av dator.
- Bottenarean för en kropp är en cirkel, vars radie är 4. När man bildar tvärsnittsareor får man liksidiga trianglar. Bestäm volymen av kroppen.
På avståndet \( x \) är halva längden för en sida på triangeln \( y = \sqrt{4^2-x^2} \).
Med hjälp av Pythagoras får vi att höjden, \( h = \sqrt{3}y \).
Funktionen som ger tvärsnittsarean är \( A(x) = \sqrt{3}(16-x^2) \).
Volymen är \( V = \displaystyle\int_{-4}^{4} A(x) \textrm{ d}x = \ldots = \dfrac{256{\sqrt{3}}}{3} \approx 148 \).
- För vilket värde på \( a \) får arean som bildas mellan \( f(x)=\sin^2 x \cos x \) och \( x \)-axeln i intervallet \( [0,a] \) värdet \( \dfrac{1}{24} \)?
Du skall lösa ekvationen \( \displaystyle\int_0^a \sin^2x \cos x \text{ d}x = \dfrac{1}{24} \).
Ritar du upp funktionen märker du att den har en viss symmetri. Integralen från 0 till \( \dfrac{\pi}{2} \) har värdet \( \dfrac{1}{3} \). Det betyder att det värde på \( a \) som vi söker är mindre än \( \dfrac{\pi}{2} \).
Integrera och lös ekvationen. Du kommer fram till \( a = \dfrac{\pi}{6} \).
Löser du ekvationen på CAS så tag och stäng in lösningarna i ett intervall, det gör saken lättare.
- Bottnet för en kropp är en halvcirkel vars radie är 4. Tvärsnittsareorna för kroppen är kvadrater som är vinkelräta mot diagonalen. Bestäm volymen för kroppen.
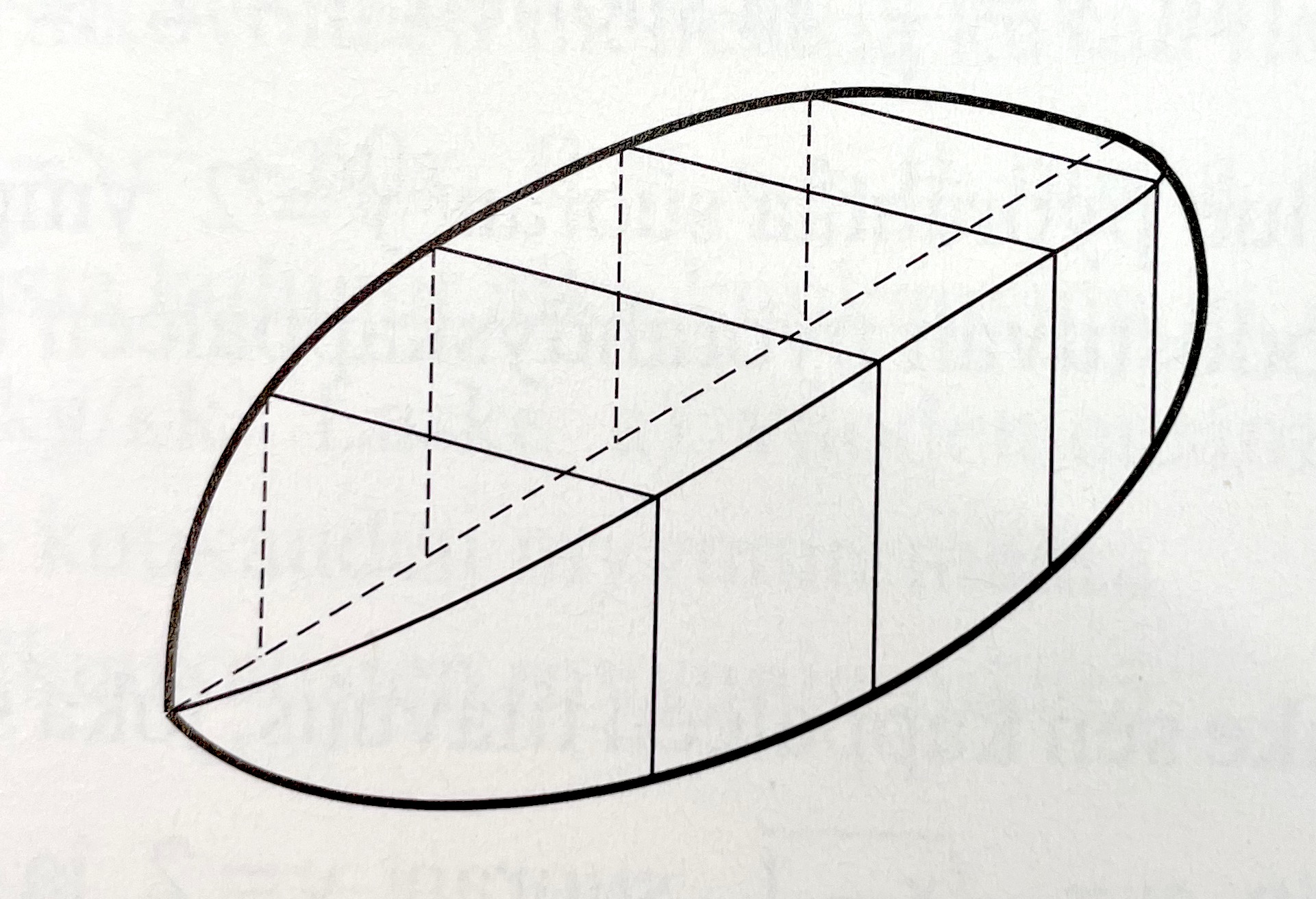
Placera mitten av diagonalen i origo. Då är längden av sidan för tvärsnittskvadraterna \( \sqrt{16-x^2} \).
Volymen är \( V = \displaystyle\int_{-4}^4 \sqrt{16-x^2}^2 \text{ d}x = \dfrac{256}{3} = 85\dfrac{1}{3} \).
- Bestäm storleken av det område som bildas mellan \( y \)-axeln och \( f(x)=\sqrt{x-1} \) då \( 1\leq x \leq 5 \).
Den inversa funktion som vi arbetar med är \( y=\sqrt{x-1} \Leftrightarrow y^2=x-1 \Leftrightarrow x = y^2+1 \)
För \( f(1)=0 \) och \( f(5)=2 \).
Området har storleken \( \displaystyle\int_0^2 y^2+1 \mathrm{ d}y = \bigg/_0^2 \dfrac{1}{3}y^3+y =(\dfrac{1}{3}\cdot 2^3+2)-(\dfrac{1}{3}\cdot 0^3+0) = 4\dfrac{2}{3} \).