10. Arean mellan två funktioner

Bestäm arean som bildas mellan \( f(x)=x^2-3x+3 \) och \( g(x)=-x+6 \).

Lösning

Området som bildas är skillnaden mellan \( \displaystyle\int -x+6 \mathrm{ d}x \) och \( \displaystyle\int x^2-3x+3\mathrm{ d}x \).

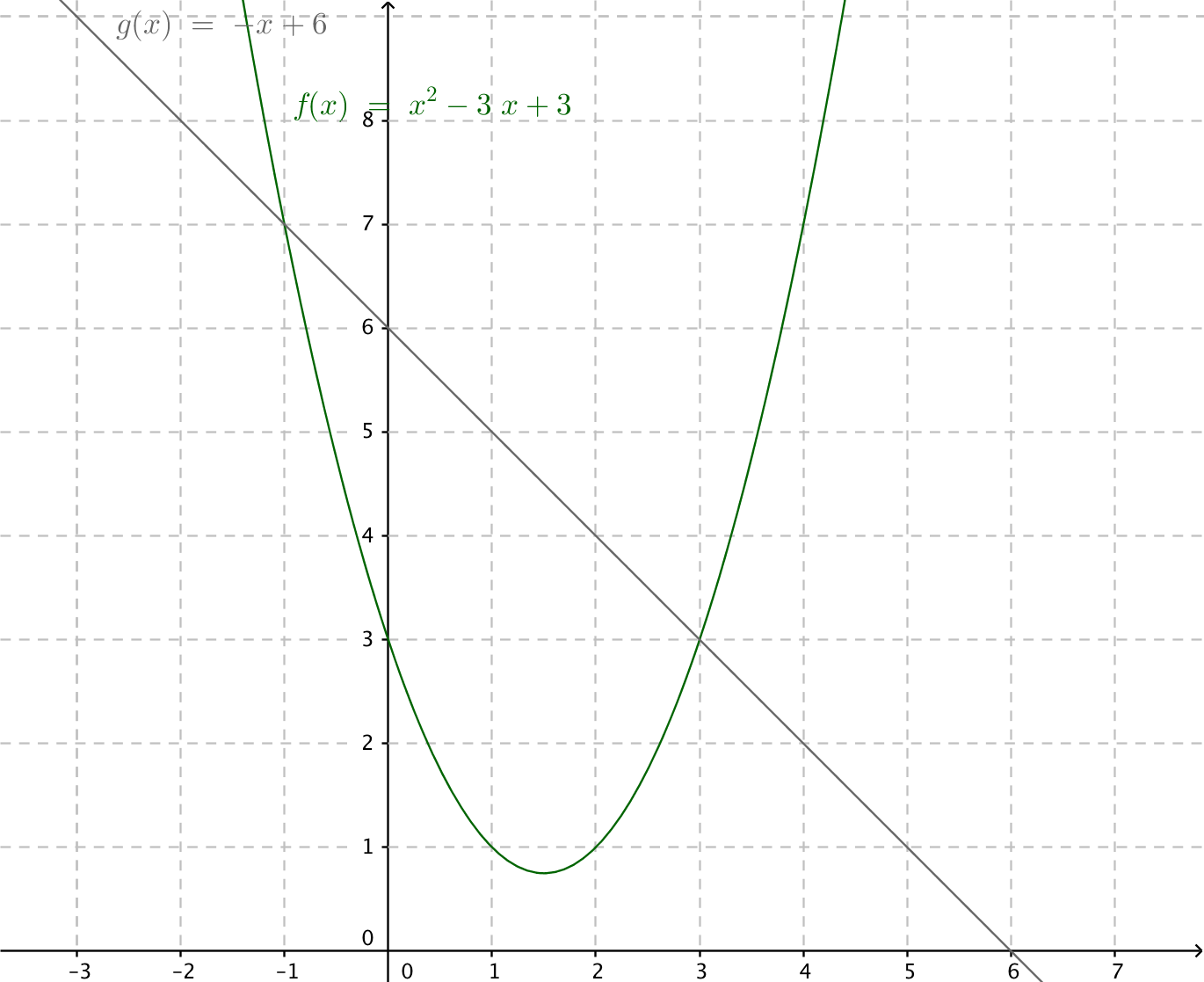
Vi behöver skärningspunkterna,

\( \begin{array}{rcl} f(x) & = & g(x) \\ x^2-3x+3 & = & -x+6 \\ x^2 -2x-3 & = & 0 \\ x & = & \dfrac{2\pm \sqrt{(-2)^2-4\cdot 1 (-3)}}{2\cdot 1} \\ x & = & \dfrac{2\pm 4}{2}\\ \end{array} \)

Skärningspunkterna är \( x=-1 \) och \( x=3 \).

Arean är

\( \begin{array}{rcl} \displaystyle\int_{-1}^3 -x+6 \mathrm{ d}x -\displaystyle\int_{-1}^3 x^2-3x+3 \mathrm{ d}x & = & \displaystyle\int_{-1}^3 -x+6 -(x^2-3x+3) \mathrm{ d}x\\ & = & \displaystyle\int_{-1}^3 -x^2+2x+3 \mathrm{ d}x \\ & = & \bigg/_{-1}^3 -\dfrac{1}{3}x^3+x^2+3x \\ & = & (-\dfrac{1}{3}\cdot 3^3+3^2+3\cdot 3)- (-\dfrac{1}{3}\cdot (-1)^3+(-1)^2+3\cdot (-1))\\ & = & 9-(-1\dfrac{2}{3}) = 10\dfrac{2}{3}\\ \end{array} \)

Då vi bestämmer arean mellan två funktioner, \( f(x) \) och \( g(x) \) i intervallet \( [a,b] \) där \( f(x) > g(x) \) räknar vi som \( A=\displaystyle\int_a^b f(x)-g(x) \mathrm{ d}x \).

Om det är så att en del av den gemensamma arean blir under \( x \)-axeln kan vi flytta funktionerna uppåt genom att addera till ett \( n \).

Storleken av arean ändras inte genom att vi flyttar funktionerna uppåt. Vi får då att \( \displaystyle\int_a^b (f(x)+n)-(g(x)+n) \mathrm{ d}x = \displaystyle\int_a^b f(x)+n -g(x)-n \mathrm{ d} x = \displaystyle\int_a^b f(x)-g(x) \mathrm{ d} x \).

Exempel 1 Mellan \( f(x)=\sin 2x \) och \( g(x)=\cos 2x \) uppstår oändligt många areor. Bestäm storleken av en area.

Lösning

Funktionerna beter sig som följande:

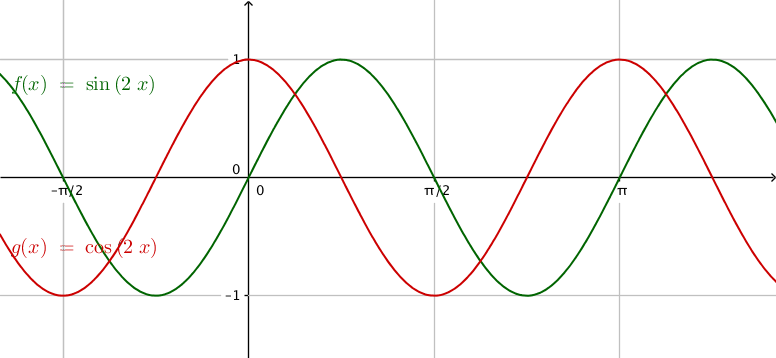
Först söker vi skärningspunkterna,

\( \begin{array}{rcll} \sin 2x & = & \cos 2x & | /\cos2x\not=0 \\ \dfrac{\sin 2x}{\cos 2x} & = & 1 \\ \tan 2x & = & 1\\ 2x & = & \dfrac{\pi}{4} + n\cdot \pi\\ x & = & \dfrac{\pi}{8} + n\cdot \dfrac{\pi}{2}, n\in \mathbf{Z}\\ \end{array} \)

En area bildas mellan skärningspunkterna \( \dfrac{\pi}{8} \) och \( \dfrac{\pi}{8} + 1 \cdot \dfrac{\pi}{2} = \dfrac{5\pi}{8} \).

Arean är

\( \begin{array}{rcl} \displaystyle\int_{\dfrac{\pi}{8}}^{\frac{5\pi}{8}} \sin 2x - \cos 2x \mathrm{ d} x & = & \displaystyle\int_{\dfrac{\pi}{8}}^{\frac{5\pi}{8}} \dfrac{1}{2}\cdot 2\sin 2x - \dfrac{1}{2}\cdot 2\cos 2x \mathrm{ d} x \\ & = & \dfrac{1}{2}\displaystyle\int_{\dfrac{\pi}{8}}^{\frac{5\pi}{8}} 2\sin 2x - 2\cos 2x \mathrm{ d} x \\ & = & \dfrac{1}{2}\bigg/_{\dfrac{\pi}{8}}^{\frac{5\pi}{8}} -\cos2x -\sin 2x \\ & = & -\dfrac{1}{2}\bigg/_{\dfrac{\pi}{8}}^{\frac{5\pi}{8}} \cos2x +\sin 2x \\ & = & -\dfrac{1}{2}[ (\cos 2\cdot \dfrac{5\pi}{8} + \sin 2\cdot\dfrac{5\pi}{8})-(\cos 2\cdot \dfrac{\pi}{8} + \sin 2\cdot\dfrac{\pi}{8})] \\ & = & -\dfrac{1}{2}[(-\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{2}})-(\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}})] \\ & = & -\dfrac{1}{2}(-\dfrac{2}{\sqrt{2}}-\dfrac{2}{\sqrt{2}})\\ & = & -\dfrac{1}{2}\cdot (-\dfrac{4}{\sqrt{2}}) \\ & = & \dfrac{2}{\sqrt{2}} = \sqrt{2} \approx 1,41 \\ \end{array} \)

Uppgifter

Bestäm arean som bildas mellan följande funktioner.
1. \( y=x^2-2 \) och \( y = -2x^2+1 \).
  
  Situationen är följande
  
  Skräningspunkterna är \( x^2 -2 = -2x^2 +1 \), \( x_1 = -1 \) och \( x_2 = 1 \). Se till att du löser dem, inte avläser från grafen.
  
  \( \begin{array}{rcl} A & = & \displaystyle\int_{-1}^{1} -2x^2+1 - (x^2-2) \textrm{ d}x \\ & = & \displaystyle\int_{-1}^{1} -3x^2+3 \textrm{ d}x \\ & = & \bigg/_{-1}^{1} -x^3+3x \\ & = & -1^3+3\cdot 1 -(-(-1)^3+3(-1)) \\ & = & -1 + 3 -(1-3) = 4 \text{ a.e.}\\ \end{array} \)
2. \( y = x-2 \) och \( y=-x^2+3x+1 \).
  
  Situationen är följande
  
  Skräningspunkterna är \( x -2 = -x^2 +3x+1 \), \( x_1 = -1 \) och \( x_2 = 3 \). Se till att du löser dem, inte avläser från grafen.
  
  \( \begin{array}{rcl} A & = & \displaystyle\int_{-1}^{3} -x^2+3x+1 -(x-2) \textrm{ d}x \\ & = & \displaystyle\int_{-1}^{3} -x^2+2x+3 \textrm{ d}x \\ & = & \bigg/_{-1}^{3} -\dfrac{1}{3}x^3+x^2+3x \\ & = & -\dfrac{1}{3}\cdot 3^3+3^2+3\cdot 3 -(-\dfrac{1}{3}\cdot (-1)^3+(-1)^2+3(-1)) \\ & = & 9 -(-1\dfrac{2}{3}) = 10\dfrac{2}{3} \text{ a.e.}\\ \end{array} \)
3. \( y=-x^2+x+2 \) och \( y = x^2 -x -2 \).
  
  Situationen är följande
  
  Skräningspunkterna är \( -x^2+x+2 = x^2 -x-2 \), \( x_1 = -1 \) och \( x_2 = 2 \). Se till att du löser dem, inte avläser från grafen.
  
  \( \begin{array}{rcl} A & = & \displaystyle\int_{-1}^{2} -x^2+x+2 -(x^2-x-2) \textrm{ d}x \\ & = & \displaystyle\int_{-1}^{2} -2x^2+2x+4 \textrm{ d}x \\ & = & \bigg/_{-1}^{2} -2\dfrac{1}{3}x^3+x^2+4x \\ & = & -2\dfrac{1}{3}\cdot 2^3+2^2+4\cdot 2 -(-2\dfrac{1}{3}\cdot (-1)^3+(-1)^2+4(-1)) \\ & = & 6\dfrac{2}{3} - (-2\dfrac{1}{3}) = 9 \text{ a.e.} \\ \end{array} \)
Bestäm storleken av arean som uppstår mellan \( f(x)=-x^2+5x+1 \) och \( g(x)=2x+1 \) i intervallet \( [1,3] \).

Vi får \( \displaystyle\int_1^3 -x^2+5x+1-(2x+1) \mathrm{ d} x = \displaystyle\int_1^3 -x^2+3x \mathrm{ d}x = \bigg/_1^3 -\dfrac{1}{3}x^3+\dfrac{3}{2}x^2 = 3\dfrac{1}{3} \) a.e.
Bestäm storleken av arean som uppstår mellan \( f(x)=-x^2+5x \) och \( g(x)=-x+5 \).

Skärningspunkterna är 1 och 5. Arean är \( \displaystyle\int_1^5 -x^2+5x-(-x+5) \mathrm{ d} x= \displaystyle\int_1^5 -x^2 +6x -5 \mathrm{ d} x = \bigg/_1^5 -\dfrac{1}{3}x^3+3x^2-5x = 10\dfrac{2}{3} \) a.e.
Bestäm storleken av arean som uppstår mellan \( f(x)=-x^2+2x+4 \) och \( g(x)=x^2-4x+4 \).

Skärningspunkterna är 0 och 3 (bestäm dem!). Arean är \( \displaystyle\int_0^3 -x+2x+4 -(x^2-4x+4) \mathrm{ d}x = \displaystyle\int_0^3 -2x^2+6x \mathrm{ d}x = \bigg/_0^3 -\dfrac{2}{3}x^3+3x^2 = 9 \) a.e.
Bestäm storleken av arean som bildas mellan parabeln \( y = x^2 \), tangenten för \( f \) som går genom punkten \( (1,1) \) och \( y \)-axeln.

Situationen är följande

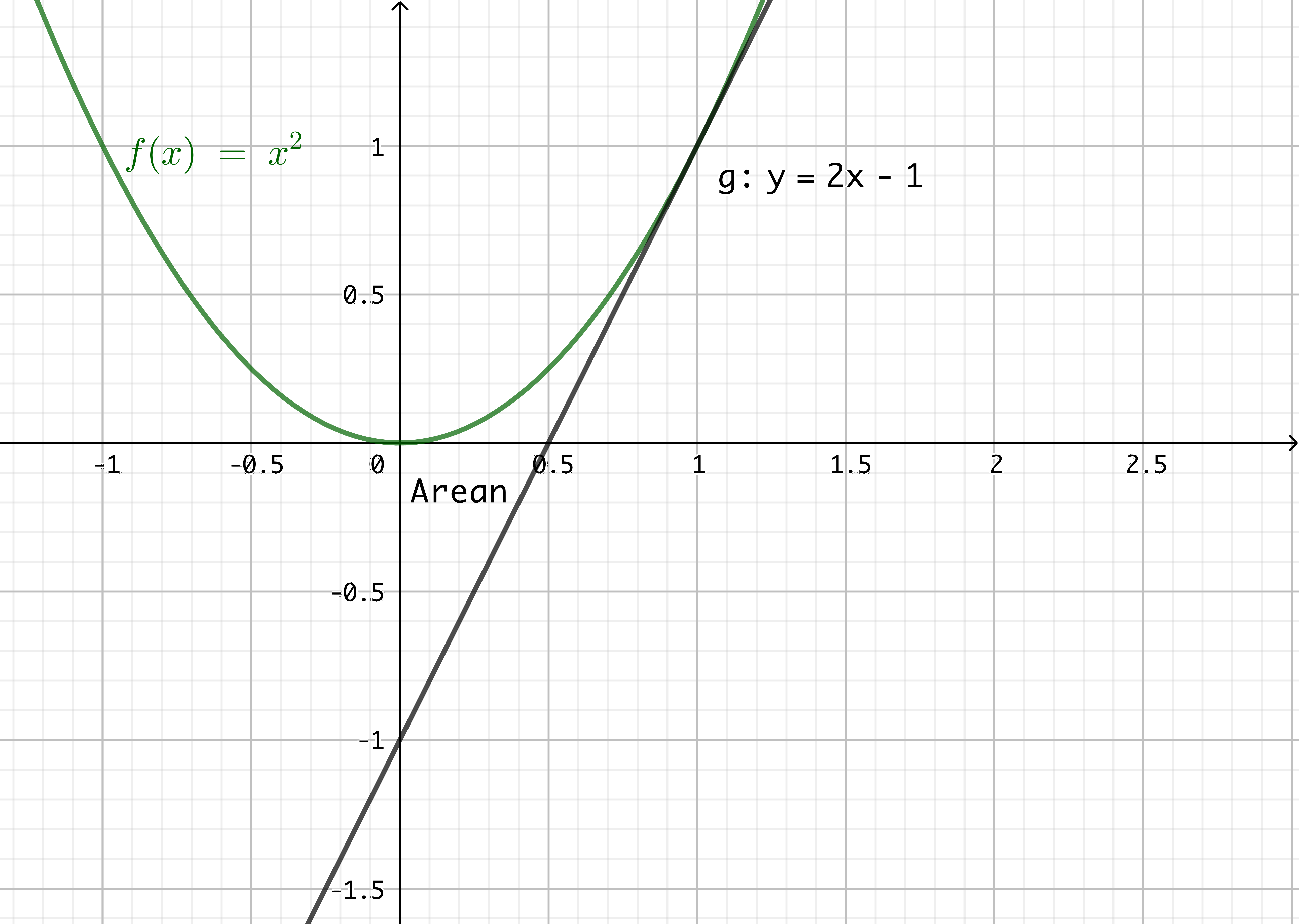
Storleken av arean är \( \displaystyle\int_0^1 x^2-(2x-1) \mathrm{ d}x = \dfrac{1}{3} \).
Bestäm storleken av arean som uppstår mellan \( y=e^{-x} \), \( y=e^{\frac{x}{2}} \) och \( x=3 \).

Börja med att rita upp situationen!

Skärningspunkten för \( e^{-x} \) och \( e^{\frac{x}{2}} \) är \( x=0 \).

Storleken av arean är \( \displaystyle\int_0^3 e^{\frac{x}{2}}-e^{-x} \mathrm{ d}x = \bigg/_0^3 2e^{\frac{x}{2}} -(-e^{-x}) =2e^{\frac{3}{2}}+\dfrac{1}{e^3}-3\approx 1,53 \) a.e.
Mellan funktionerna \( \sin 2x \) och \( \cos 2x \) uppstår oändlig många likformiga areor. Bestäm arean av ett område.

Börja med att rita bild.

Skärningspunkterna för funktionerna är \( x = \dfrac{\pi}{8} + n\cdot \dfrac{\pi}{2} \), där \( n \) är ett heltal.

Tag ett intervall och bestäm vilken funktion som är ovan. Bilda sedan ett uttryck och integrera det. Kom fram till \( \sqrt{2} \).
Bestäm storleken av arean som uppstår mellan \( f(x)=-x+3 \) och \( g(x)=\dfrac{1}{x} \).
Denna uppgift löser du lättast på räknare. Du märker snart varför.

Skärningspunkterna är \( f(x)=g(x) \Leftrightarrow x=\dfrac{3\pm\sqrt{5}}{2} \).

Arean är \( \displaystyle\int_{\frac{3-\sqrt{5}}{2}}^{\frac{3+\sqrt{5}}{2}} -x+3-\dfrac{1}{x} \mathrm{ d}x =\bigg/_{\frac{3-\sqrt{5}}{2}}^{\frac{3+\sqrt{5}}{2}} -\dfrac{1}{2}x^2+3x-\ln x \approx 1,43 \).
För vilket värde på konstanten \( a \) gäller att det området som bestäms av \( f(x)=ax \) och \( g(x)=x^2 \) har värdet 36?

Skärningspunkten mellan \( f \) och \( g \) är

\( \begin{array}{rcl} ax & = & x^2 \\ x^2-ax & = & 0 \\ x(x-a) & = & 0\\ \end{array} \)
Alltså \( x=0 \) och \( x=a \).

Vi får att för arean gäller

\( \begin{array}{rcl} \displaystyle\int_0^a ax-x^2 \mathrm{ d}x & = & 36 \\ \bigg/_0^a \dfrac{a}{2}x^2-\dfrac{1}{3}x^3 & = & 36 \\ (\dfrac{a^3}{2}-\dfrac{a^3}{3})-(\dfrac{a}{2}\cdot 0^2-\dfrac{1}{3}\cdot 0^3) & = & 36 \\ \dfrac{a^3}{6}-0 & = & 36 \\ a & = & \sqrt[3]{3\cdot 36} = 6\\ \end{array} \)

Eftersom funktionerna är symmetriska kring \( x \)-axeln gäller att \( a=\pm 6 \).
Bestäm storleken av området som bildas mellan \( y=x^2 \), tangenten för \( y=x^2 \) i punkten \( (1,1) \) och \( y \)-axeln.

Tangenten för \( f(x)=x^2 \) i punkten \( 1 \) har riktningskoefficienten \( f'(1) = 2\cdot 1 = 2 \). Tangentens ekvation är \( y-y_0 = k(x-x_0) \Leftrightarrow y=2x-1 \).

Skärningspunkten för \( f(x)=x^2 \) och \( y=2x-1 \) är \( x^2=2x-1 \Leftrightarrow x=1 \).

För att bestämma arean integrerar vi från \( x=0 \) till \( x=1 \). Arean är \( \displaystyle\int_0^1 x^2-(2x-1) \mathrm{ d}x = \displaystyle\int_0^1 x^2-2x+1 \mathrm{ d} x = \bigg/_0^1 \dfrac{1}{3}x^3-x^2+x =(\dfrac{1}{3}\cdot 1^3-1^2+1)-(\dfrac{1}{3}\cdot 0^3-0^2+0) = \dfrac{1}{3} \) a.e.
Ett område bestäms av \( f(x)=\dfrac{1}{x^2} \), \( g(x)=\dfrac{1}{x^3} \) och linjerna \( x=a \) och \( x=2a \) där \( a > 0 \). För vilket värde på \( a \) har området ett så stort värde som möjligt?

Linjerna utgör gränserna. Så arean är \( \displaystyle\int_a^{2a} \dfrac{1}{x^2} -\dfrac{1}{x^3} \mathrm{ d}x =\bigg/_a^{2a} \dfrac{1}{-1}x^{-1} -\dfrac{1}{-2}x^{-2}= \bigg/_a^{2a} -\dfrac{1}{x}+\dfrac{1}{2x^2} = -\dfrac{1}{2a}+\dfrac{1}{2(2a)^2}-(-\dfrac{1}{a}+\dfrac{1}{2\cdot a^2}) = \dfrac{1}{2a}-\dfrac{3}{8a^2} \).

Det vad vi har är en funktion som ger arean. Vi betecknar den \( A(a)=\dfrac{1}{2a}-\dfrac{3}{8a^2} \). För att bestämma största värde undersöker vi funktionen. \( A'(a)=-\dfrac{1}{2a^2}+\dfrac{3}{4a^3} \). \( A'(a)=0 \) då \( a=\dfrac{3}{2} \).

Då \( A'(1)= \dfrac{1}{4} > 0 \) och \( A'(2)=-\dfrac{1}{32} < 0 \) är \( a=\dfrac{3}{2} \) ett maximum.
Funktionen \( f(x)=x^3 \) och normalen för funktionen i punkten \( (a,a^3) \), \( a > 0 \), avbegränsar ett område. Vilket värde närmar sig områdets area då \( a \) närmar sig noll från höger?

Vi har följande situation.

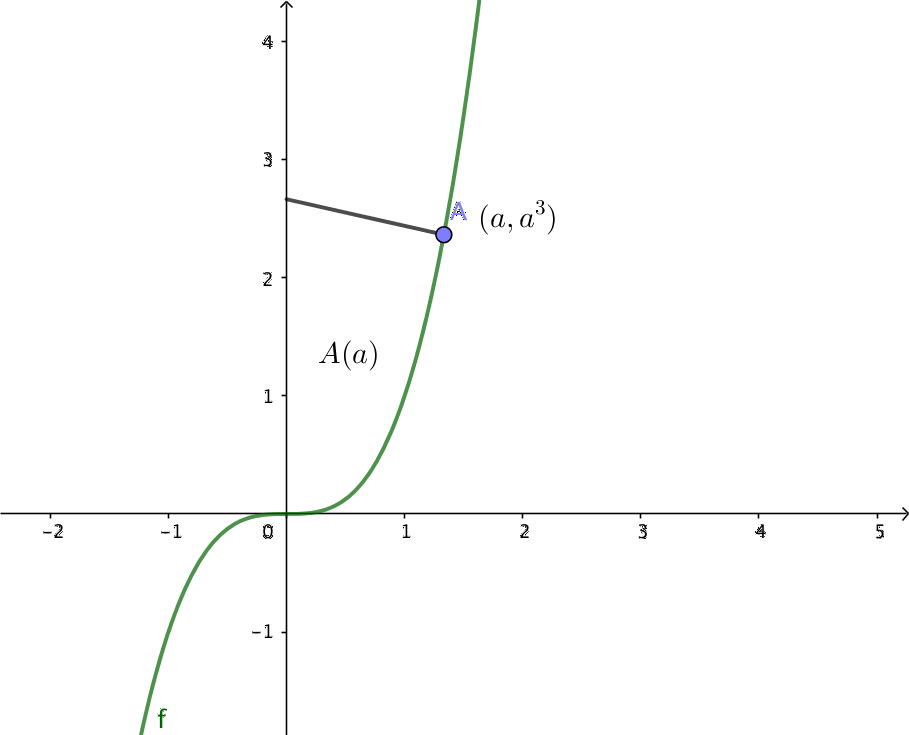
Normalen ekvation är av typ \( y-y_0 = k(x-x_0) \). Punkten som tangenten går igenom är \( (a,a^3) \).

\( f'(x) = 3x^2 \). Tangentens riktningskoefficient i punkten \( a \) är \( 3a^2 \), normalens riktningskoefficient är \( -\dfrac{1}{3a^2} \).

Normalens ekvaiton är \( y = -\dfrac{1}{3a^2}x +\dfrac{1}{3a}+a^3 \).

Områdets area är från \( 0 \) till \( a \). Vi får

\( \begin{array}{rcl} A(a) & = & \displaystyle\int_{0}^{a} -\dfrac{1}{3a^2}x +\dfrac{1}{3a}+a^3 - x^3 \textrm{ d}x \\ & = & \bigg/_{0}^{a} -\dfrac{1}{6a^2}x^2 +\dfrac{1}{3a}x+a^3x -\dfrac{1}{4} x^4 \\ & = & \dfrac{3}{4}a^4 + \dfrac{1}{6} \\ \end{array} \)

Då \( a \) närmar sig 0 från höger får vi \( \lim_{a \to 0_{+}} \dfrac{3}{4}a^4 + \dfrac{1}{6} = \dfrac{3}{4}\cdot 0^4 +\dfrac{1}{6} = \dfrac{1}{6} \).