12. Allmänna volymer

Som det sista behandlar vi ännu volymer där tvärsnittsarean bildas av en funktion. Denna funktion integrerar vi över ett intervall för att få volymen för kroppen.

Exempel 1 Ett museum ser uppifrån ut som en cirkel med diametern 100 m. Tvärsnitten för muséet är rektanglar som är dubbelt så breda som höga. Bestäm volymen för museet.

Lösning

Från sidan ser det ut som

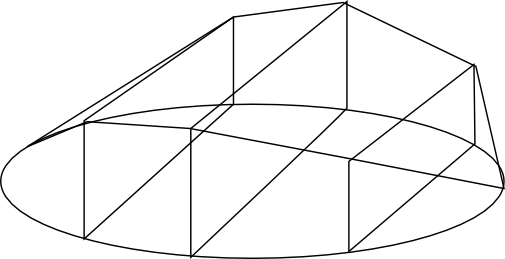
och uppifrån som

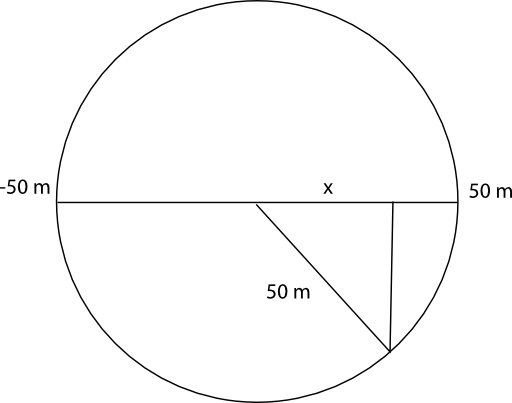
Arean för ett tvärsnitt är \( A(x)= \sqrt{50^2-x^2}\cdot 2\sqrt{50^2-x^2} = 2(50^2-x^2) \).

Volymen är

\( \begin{array}{rcl} \displaystyle\int_{-50}^{50} A(x) \mathrm{ d} x & = & 2\displaystyle\int_0^{50} A(x) \mathrm{ d} x \\ & = & 2\displaystyle\int_0^{50} 2(50^2-x^2) \\ & = & 4\displaystyle\int_0^{50} 50^2-x^2 \\ & = & 4\bigg/_0^{50} 2500x-\dfrac{1}{3}x^3 \\ & = & 4 [(2500\cdot 50-\dfrac{1}{3}\cdot 50^3)-(2500\cdot 0-\dfrac{1}{3}\cdot 0^3)]\\ & = & 333333,33 \text{ m}^3 \\ & \approx & 330000 \text{ m}^3\\ \end{array} \)

Exempel 2 Bestäm volymen för en pyramid med bottensidan \( a \) och höjden \( h \) .

Lösning

Vi tar och tänker oss pyramiden i ett koordinatsystem, där toppen är i origo och bottenarean är på avståndet \( a \). Pyramidens volym består av oändligt många kvadratiska skivor, där den nedersta har arean \( a^2 \).

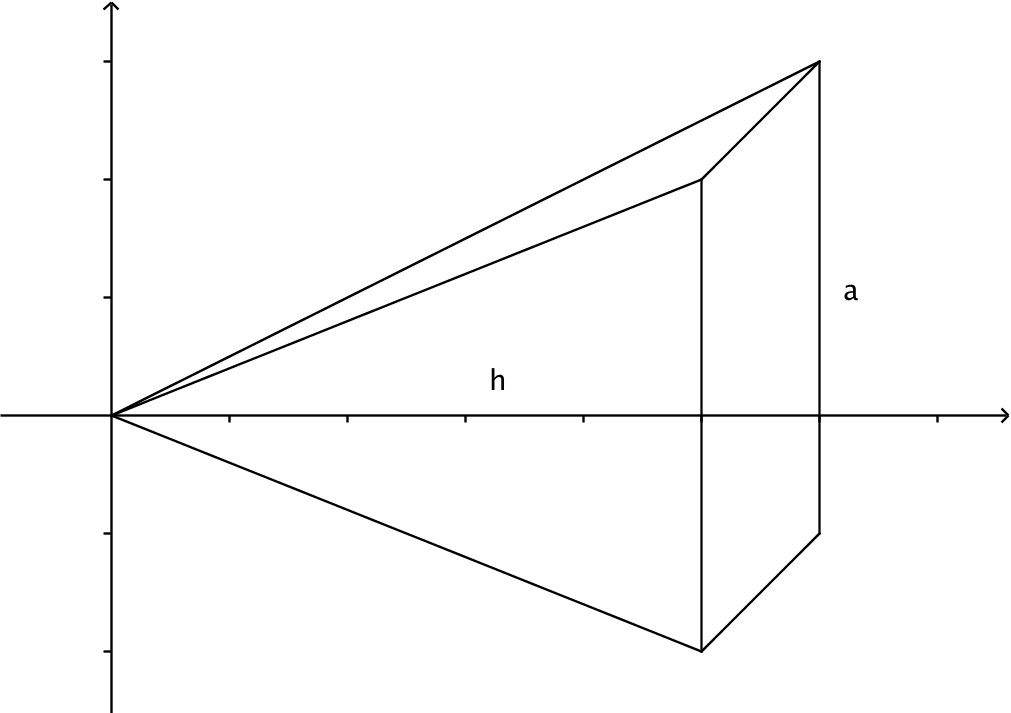
Vi kan addera ihop dessa kvadratiska sidor med hjälp av integrering från \( 0 \) till \( h \).

På ett visst avstånd \( x \) gäller att höjden \( y \) är likformig med \( a \) och \( h \). Vi får att \( \dfrac{A(x)}{a^2}=\dfrac{x^2}{h^2} \Leftrightarrow A(x)=\dfrac{x^2a^2}{h^2} \).

Volymen är \( \displaystyle\int_0^h A(x) \mathrm{ d} x = \displaystyle\int_0^h \dfrac{a^2}{h^2} x^2 \mathrm{ d} x = \dfrac{a^2}{h^2} \bigg/_0^h \dfrac{a^2}{h^2} \dfrac{1}{3}x^3 =\dfrac{a^2}{h^2}(\dfrac{1}{3}\cdot h^3 -\dfrac{1}{3}\cdot 0^2) = \dfrac{1}{3}ha^2 \).

För att bestämma volymer med hjälp av integraler behöver vi en funktion som anger arean vid en bestämd punkt. Sedan är det bara att integrera. Volymen får vi som

\( \displaystyle\int_a^b A(x)\mathrm{ d}x \).

Uppgifter

Tvärsnittsarean i cm² för en batong följer på ett ungefär funktionen \( A(x) = 11x-0,35x^2 \), var \( 0 \leq x \leq 30 \). Bestäm volymen för batongen.

Vi får \( V = \displaystyle\int_{0}^{30} 11x-0,35x^2 \textrm{ d}x = 1800 \) cm³.

Alltså 1,8 dm³ eller 1,8 l.
Höjden för en förpackning är 0,5 m och tvärsnittsarean som följer bottnet är kvadratisk av sig. På höjden \( x \) är längden för sidan \( 2x+1 \) meter. Bestäm volymen av förpackningen.

Funktionen som ger tvärsnittsarean är \( A(x) = (2x+1)^2 \).

\( V = \displaystyle\int_0^{0,5} (2x+1)^2 \textrm{ d}x = 1,166\ldots \) m³
.
Alltså 1,2 m³
Tvärsnitten för en vas består av kvadratiska skivor där sidan har längden \( 3+\sqrt{x} \) på höjden \( x \) cm. Bestäm vasens volym då den är 25 cm hög.

Arean för en tvärsnittsarea är \( A(x)=(3+\sqrt{x})^2 \) där \( 0\leq x \leq 25 \).

Volymen är \( \displaystyle\int_0^{25} A(x) \mathrm{ d}x = \displaystyle\int_0^{25} (3+\sqrt{x})^2 \mathrm{ d} x = \displaystyle\int_0^{25} 9+6\sqrt{x} +x \mathrm{ d} x = \bigg/_0^{25} 9x + 6\cdot \dfrac{2}{3}\cdot x \sqrt{x} +\dfrac{1}{2}x^2 = 1037,5 \text{ cm}^3 = 1,04 \text{ dm}^3 \).
Formen för en kropp följer kurvan \( \dfrac{4}{x} \) då \( 1\leq x \leq 4 \) så att tvärsnittsarean bildar liksidiga trianglar där höjden är \( \dfrac{4}{x} \). Bestäm volymen för kroppen.

På avståndet \( x \) är höjden för tvärsnittet \( \dfrac{4}{x} \).
Antingen kan vi utnyttja likformighet eller Pythagoras för att få ett förhållande mellan basytan och höjden.

Då höjden är \( h = f(x) \) och basytans längd är \( b \) kan vi bilda förhållandet \( \dfrac{h}{b} \). Eftersom triangeln är liksidig kan vi arbeta med Typtriangel 2. Då gäller att \( \dfrac{h}{b} = \dfrac{\sqrt{3}}{2} \). Då \( h = f(x) \) får vi att basytan är \( \dfrac{4}{x}=\dfrac{b\sqrt{3}}{2} \Leftrightarrow b=\dfrac{8}{x\sqrt{3}} \).

Arean för tvärsnitten är \( A(x)=\dfrac{1}{2}\cdot \dfrac{8}{x\sqrt{3}} \cdot \dfrac{4}{x} = \dfrac{16}{x^2\sqrt{3}} \).

Volymen är \( \displaystyle\int_1^4 A(x)=\mathrm{ d} x = \displaystyle\int_1^4 \dfrac{16}{x^2\sqrt{3}} \mathrm{ d}x = \dfrac{16}{\sqrt{3}} \bigg/_1^4 -\dfrac{1}{x} = 4\sqrt{3} \).
Bottnet för en idrottshall har formen av en cirkel vars diameter är 84 meter. Tvärsnittsarean för idrottshallen bildar kvadrater. Bestäm volymen för idrottshallen.

Vi placerar \(x\)-axeln så att den går längs med diametern så att origo är i mitten av hallen. Vi punkten \( x \) har tvärsnittsareorna längden \( 2\sqrt{42^2-x^2} \) där \( -42 \leq x \leq 42 \).

Volymen är \( \displaystyle\int_{-42}^{42}(2\sqrt{42^2-x^2})^2 \textrm{ d}x \approx 395 100 \text{ m}^3 \).
Längderna i centimeter för sidorna för en matförpackning med kvadratiska tvärsnittsareor följer funktionen \( x+5 \). Bestäm höjden för förpackningen med en mm noggrannhet då man vill att den skall rymma 4,5 dl.

4,5 dl motsvaras av 450 cm³.

Storleken av tvärsnittsarean är \( A(x)=(x+5)^2 \).

Vi får ekvationen \( \displaystyle\int_0^a (x+5)^2 = 450 \) som har lösningen \( a\approx 6,38 \) cm.

Alltså 6,4 cm.
Höjden för en kruka är 1,0 m. Tvärsnitten paralella med bottenytan bildar kvadrater. På höjden \( x \) meter är sidans längd \( e^x \). Bestäm volymen för krukan.

Funktionen som ger tvärsnittet är \( A(x) = (e^x)^2 = e^{2x} \).

Volymen är \( \displaystyle\int_0^{1} e^{2x} \textrm{ d}x = \dfrac{e^2-1}{2} \approx 3,1945 \) m³.

Alltså 3200 liter.
Tvärsnittet av ett tält är en likbent triangel där basen är är en och en halv gånger så lång som höjden. Tältet är 3,0 m långt och gavlarna har höjden 1,0 m och 1,5 m. Takåsen i tältet har formen av en parabel med toppen i den lägre gavelns hörn.

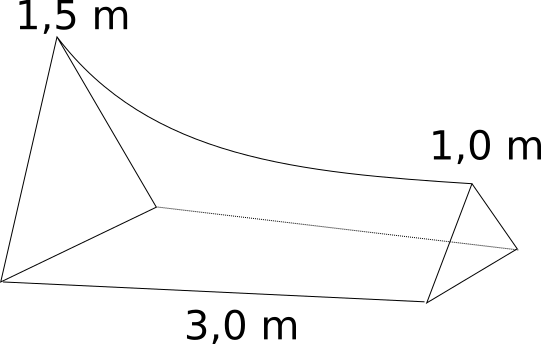
Beräkna tältets volym i liter.

Arean för en triangel är \( A=\dfrac{1}{2}bh \). Då vi vet höjden \( h \) är basen \( 1,5h \). Alltså är \( A=\dfrac{1}{2}\cdot 1,5 h^2 = \dfrac{3}{4}h^2 \).
Höjden för tältet följer en parabel. Vi flyttar parabeln så att toppen av parabeln går genom origo. Då går parabeln genom punkterna \( (0,0) \) och \( (3;0,5) \). Parabelns ekvation är \( f(x)=\dfrac{1}{18}x^2 \). Då vi lyfter upp den ett steg får vi \( f(x)=\dfrac{1}{18}x^2+1 \).

Funktionen som ger tvärsnittsarean är \( A(x)=\dfrac{3}{4} (\dfrac{1}{18}x^2+1)^2 \).

Volymen är \( \displaystyle\int_0^3 A(x) \mathrm{\, d} x = \displaystyle\int_0^3 \dfrac{3}{4} (\dfrac{1}{18}x^2+1)^2 \mathrm{\, d} x = 3,1125 \text{ m}^3 \).

Alltså 3 100 liter.
Tvärsnittsytorna för en kropp är likformiga bottenarean. Bottenarean har ytan \( A \) och höjden för kroppen är \( h \). Bestäm volymen för kroppen.

Vi får volymen \( \displaystyle\int_0^h A \textrm{ d}x= \bigg/_0^h Ax = Ah-A\cdot0 = Ah \).

Märk att du har härlett fram formeln för volymen för ett prisma.
Härled volymen för en rak cirkulär kon.

Vi placerar konen med spetsen i origo och höjden längs med \( x \)-axeln.

Vi höjden \( h \) är basarean \( \pi r^2 \), vid en höjd \( x \) är basarean \( A(x) \). Dessa är likformiga och vi får att \( \dfrac{A(x)}{\pi r^2}=(\dfrac{x}{h})^2 \). Vidre får vi att \( A(x)=\dfrac{\pi r^2 x^2}{h^2} \).

Volymen är \( \displaystyle\int_0^h A(x)\mathrm{ d}x = \displaystyle\int_0^h \dfrac{\pi r^2 x^2}{h^2} \mathrm{ d}x = \dfrac{\pi r^2}{h^2}\displaystyle\int_0^h x^2 \mathrm{ d}x = \dfrac{\pi r^2}{h^2} \bigg/_0^h \dfrac{1}{3}x^3 = \dfrac{\pi r^2}{3h^2}(h^3-0^3) = \dfrac{1}{3}\pi r^2 h \).