7. Tangent
Vårt nästa steg inom derivering är att bestämma tangenter för funktioner. Med hjälp av dessa tangenter, och speciellt deras riktningskoefficienter, kan vi börja analysera funktioner.
Exempel 1 Bestäm ekvationen för tangenten för funktionen \( f(x)=\dfrac{1}{3}x^3-2x-3 \) i punkten 1.
Exempel 2 Bestäm de tangenter som har riktningskoefficienten 1 för funktionen \( f(x)=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2+x \).
Då vi bestämmer derivatans värde i någon punkt så bestämmer vi värdet för tangentens riktningskoefficient i denna punkt. Derivatan ger riktningskoefficienten för tangenten.
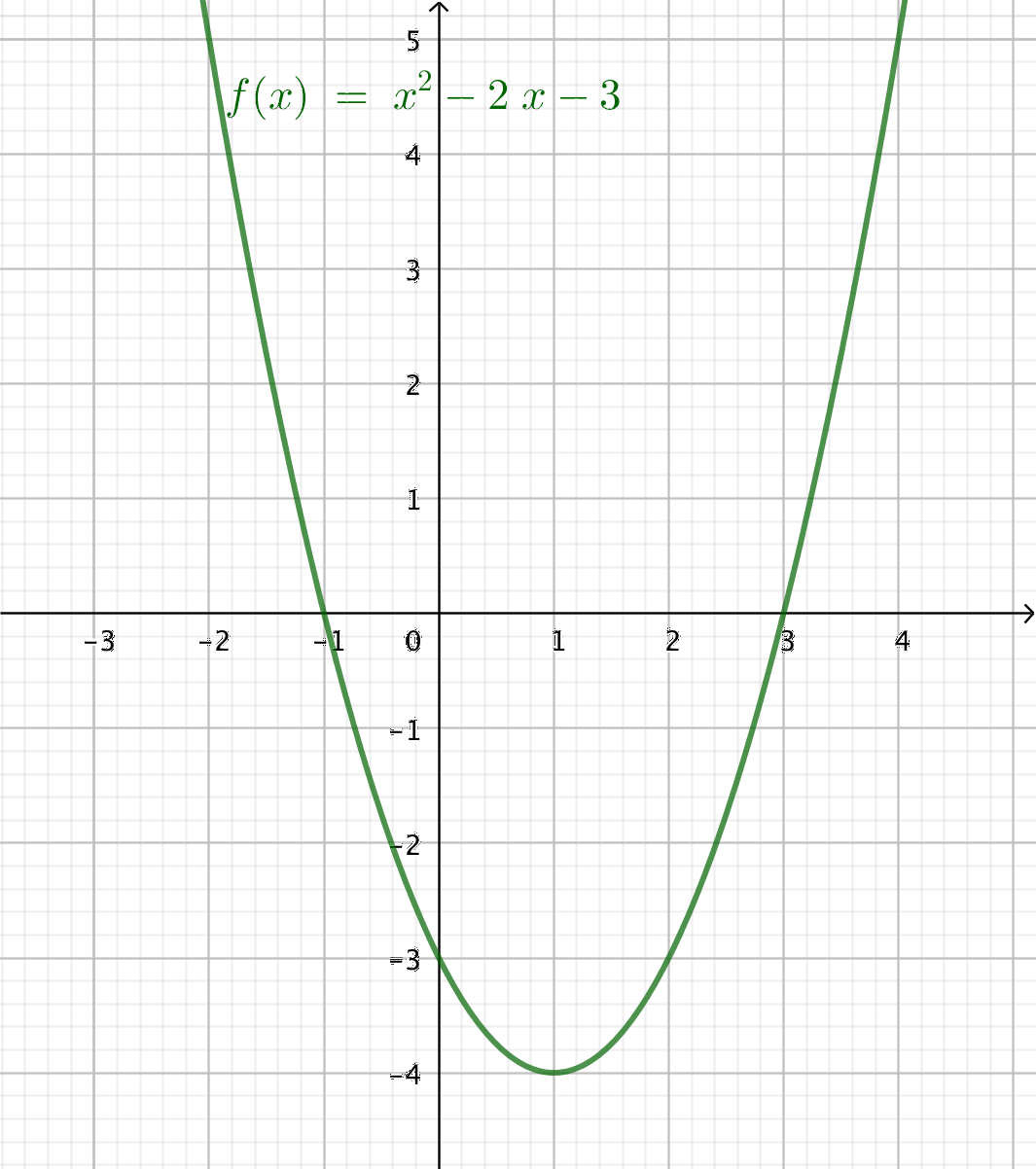
Exempel 3 Bestäm toppen för parabeln som bestäms av \( f(x) = x^2-2x-3 \).
Lösning
Eftersom parabeln byter riktning vid toppen söker vi toppens koordinat med hjälp av derivatan. I toppen är derivatans värde 0.
Vi börjar med att derivera, \( f'(x)=2x-2\).
Sedan söker vi derivatans nollställe, \( f'(x)=0 \). Alltså \( 2x-2=0 \), då \( x = 1 \).
Till sist bestämmer vi \( y \)-koordinaten, \( f(1)=1^2-2\cdot 1 -3 = -4 \).
Toppens koordinat är \( (1,-4) \).
Uppgifter
- Bestäm för funktionen \( f(x) = x^2-3x \) ekvationen för
- tangenten
Tangentens ekvation är av typ \( y-y_0 = k(x-x_0) \).
Då \( x = 1 \) är \( f(1) = 1^2-3\cdot 1 = -2 \).
Tangenten går genom \( (1,-2) \).
Derivatafunktionen är \( f'(x) = 2x-3 \).
Riktningskoefficenten för tangenten är \( f'(1) = 2\cdot 1 -3 = -1 \).
Tangentens ekvation är \( y-(-2)=-1(x-1) \Leftrightarrow y = -x-1 \).
- normalen
Punkten är samma som ovan, \( (1,-2) \).
För riktningskoefficienterna gäller att \( k_t \cdot k_n = -1 \). Alltså är riktningskoefficienten för normalen \( 1 \).
Vi får ekvationen \( y-(-2) = 1(x-1) \Leftrightarrow y = x-3 \).
- tangenten
- Bestäm för funktionen \( f(x) = x^3+2 \) ekvationen för
- tangenten
Punkten \( (0,2) \) är på funktionen. Testa själv!
Derivatafunktionen är \( f'(x) = 3x^2 \).
Tangenten i punkten \( x = 0 \) har riktningskoefficienten 0.
Tangentens ekvation är av typ \( y-y_0 =k(x-x_0) \).
Alltså \( y-2 =0(x-0) \Leftrightarrow y = 2 \).
- normalen
Eftersom tangenten saknar riktningskoefficient är normalen lodrät, av typ \( x = \ldots \).
Normalen skall genom punkten \( (0,2) \). Alltså är dess ekvation \( x = 0\).
- tangenten
- Bestäm ekvationen för tangenten för funktionen \( f(x)=x^2-x \) i punkten \( x=1 \).
\( f'(x)=2x-1 \).
Riktningskoefficienten är \( k=f'(1)=2\cdot 1 -1 = 1 \).
\( y \)-koordinaten är \( f(1) =1^2-1=0 \).
Punkten är som tangenten går igenom är (1,0).
Tangentens ekvation är \( y-y_0=k(x-x_0) \Leftrightarrow y-0=1(x-1) \Leftrightarrow y=x-1 \).
- Bestäm för funktionen \( f(x)=-x^2+6 \) ekvationen för tangenten i punkten \( x=2 \).
\( f'(x)=-2x \).
Riktningskoefficenten är \( f'(2)=-2\cdot 2 = -4 \).
\( y \)-koordinaten för tangenten är \( f(2)=-2^2+6=-4+6=2 \).
Tangenten går genom punkten \( (2,2) \).
Tangentens ekvation är \( y-y_0 =k(x-x_0) \Leftrightarrow y-2=-4(x-2) \Leftrightarrow y=-4x+10 \).
- Bestäm tangentens ekvation för funktionen \( f(x)=x^3-2x+2 \) i punkten \( x=-1 \).
\( f'(x)=3x^2-2 \)
\( k=f'(-1)=3(-1)^2-2 = 1 \).
Tangentens \( y \)-koordinat får vi via \( f(-1)=(-1)^3-2(-1)+2 =3 \). Tangenten går genom punkten \( (-1,3) \).
Tangentens ekvation är \( y-y_0=k(x-x_0) \Leftrightarrow y-3=1(x-(-1)) \Leftrightarrow y=x+4 \).
- Bestäm ekvationen för tangenten för funktionen \( f(x)=-x^3+x^2-x \) i punkten \( x=2 \).
\( f'(x)=-3x^2+2x-1 \).
Tangenten är \( k=f'(2)=-3\cdot 2^2+2\cdot 2-1 = -9 \).
Punkten som tangenten går igenom: \( f(2)= -2^3+2^2-2=-6 \). Punkten är \( (2,-6) \).
Tangentens ekvation är \( y-y_0=k(x-x_0) \Leftrightarrow y-(-6)=-9(x-2) \Leftrightarrow y=-9x+12 \).
- Bestäm de tangenter som har riktningskoefficienten 1 för funktionen \( f(x)=x^2+x \).
\( f'(x)=2x+1 \)
Vi löser ekvationen \( f'(x)=1 \) som har lösningen \( x=0 \).
\( y \)-koordinaten är då \( f(0)=0 \).
Tangentens ekvation är \( y-y_0=k(x-x_0) \Leftrightarrow y-0=1(x-0) \Leftrightarrow y=x \).
- Bestäm de tangenter för funktionen \( f(x)=\dfrac{1}{2}x^2-x \) vars riktningskoefficient har värdet 2.
\( f'(x)=\dfrac{1}{2}\cdot 2 x-1 = x-1 \)
De punkter där derivatans värde är 2 är \( f'(x)=2 \Leftrightarrow x-1 =2 \Leftrightarrow x=3 \)
\( y \)-koordinaten är \( f(3)=\dfrac{1}{2}\cdot 3^2-3 = \dfrac{3}{2} \).
Punkten är \( (3, \dfrac{3}{2}) \).
Tangentens ekvation är \( y-y_0 =k(x-x_0) \Leftrightarrow y-\dfrac{3}{2} = 2(x-3) \Leftrightarrow y=2x-4\dfrac{1}{2} \).
- Bestäm de tangenter som har riktningskoefficienten \( -1 \) för funktionen \( f(x)=\dfrac{1}{3}x^3+x^2-x \).
\( f'(x)=x^2+2x-1 \).
Vi löser ekvationen \( f'(x)=-1 \Leftrightarrow x^2+2x-1 = -1 \) som har lösningarna \( x=0 \) och \( x=-2 \).
Punkterna för tangenterna är är \( (0,0) \) och \( (-2,\dfrac{10}{3}) \) och tangenterna är \( y=-x \) och \( y=-x+\dfrac{4}{3} \).
- Bestäm de tangenter som har riktningskoefficienten 0 för funktionen \( f(x)=x^4-2x^2 \). Vad händer vid dessa punkter för funktionen?
\( f’(x)=4x^3-4x \). Vi löser ekvationen \( f'(x)=0 \Leftrightarrow 4x^3-4x = 0 \) som har lösningarna \( x=0 \) och \( x=\pm 1 \).
Tangenterna är \( y=0 \) och \( y=-1 \).
Vid dessa punkter byter funktionen riktning.
- Låt \( f(x)=-x^2-5x-7 \). Bestäm koordinaterna för parabelns topp.
Vi får \( f'(x) = -2x-5 \).
De punkter där \( f \) byter riktning är \( f'(x) = 0 \), alltså \( -2x-5 = 0 \) som är \( x = -2,5 \).
\( y \)-koordinaten är \( f(-2,5) = -(-2,5)^2-5(-2,5)-7 = -0,75 \).
Parabelns topp är i \( (-2,5 ; -0,75) \).
- Bestäm toppen för parabeln \( f(x)=-x^2+6x-9 \).
Vi får \( f'(x) = -2x+6 \)
De punkter där funktionen byter riktning är, \( f'(x) = 0 \), alltså \( -2x+6 = 0 \) som ger \( x = 3 \).
\( y \)-koordinaten är \( f(3) = -3^2+6\cdot 3 -9 = 0 \).
Toppens koordinat är \( (3,0) \).
Eftersom \( f(x) = -x^2+6x-9 = -(-x+3)^2 \) hittar man \( x \)-koordinaten även denna väg.
- Bestäm tangenten för funktionen \( f(x)=x^2 \) som går genom punkten \( (3,0) \).
Tangentens ekvation är av typ \( y-y_0 = k(x-x_0) \).
De tangenter som är på parabeln går genom punkterna \( (a,a^2) \).
Parabelns riktningskoefficeinter är av typ \( f'(x) = 2x \). Genom punkten \( a \) är riktningskoefficienten \( 2a \).
Tangentens ekvation är \( y-a^2 = 2a(x-a) \). Tangenten skall genom punkten \( (3,0) \).
Vi får ekvationen \( 0-a^2=2a(3-a) \) som har lösningarna \( a = 0 \) och \( a = 6 \).
Tangenternas ekvationer är \( y = 0 \) och \( y = 12x-36 \).
- Visa att toppen för parabeln \( f(x) = 2x^2 +6x + a \) är oberoende av värdet på \( a \).
Derivatafunktionen är \( f'(x) = 4x+6 \).
Eftersom derivatafunktionen ger de punkter där funktionen byter riktning, och vår derivatafunktion inte innehåller ett \( a \) är koordinaterna för parabeln oberoende av \( a \).