12. Derivatan av produkten mellan två funktioner
När vi deriverar produkten mellan två funktioner använder vi oss av produktregeln.
Låt oss ta funktionerna \( f \) och \( g \). Derivatan av produkten är \( D(fg) = f'g+g'f \).
Bevis
Vi tar funktionen \( h(x) \) som är produkten av \( f(x) \) och \( g(x) \), alltså \( h(x)= f(x)g(x) \). Vi skall visa att \( h'(x)=f'(x)g(x) + f(x)g'(x) \).
\( \begin{array}{rl} h'(x)= & \lim_{h \to 0} \dfrac{h(x+h)-h(x)}{h} \\ = & \lim_{h \to 0} \dfrac{f(x+h)g(x+h)-f(x)g(x)}{h} \\ = & \lim_{h \to 0} \dfrac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} \\ = & \lim_{h \to 0} \dfrac{[f(x+h)-f(x)]g(x+h)+f(x)[g(x+h)-g(x)]}{h} \\ = & \lim_{h \to 0} \dfrac{f(x+h)-f(x)}{h} \cdot \lim_{h\to 0} g(x+h)+ \lim_{h\to 0}f(x)\cdot \lim_{h\to 0}\dfrac{g(x+h)-g(x)}{h} \\ = &f'(x)g(x)+f(x)g'(x)\\ \end{array} \)
Alltså \( Df(x)g(x)=f'(x)g(x)+g'(x)f(x) \)
Exempel 1 Bestäm \( D(x^2-1)(x+1) \) genom att använda produktregeln.
När vi deriverar funktioner som består av en funktion gånger en annan funktion så får vi först förenkla och sedan derivera. Eller så får vi derivera med hjälp av produktregeln.
Derivatan av produkten mellan två funktioner är \( D f(x)g(x)=f'(x)g(x)+g'(x)f(x) \).
Vi kan också använda oss av notationen \( Dfg = f'g + g'f \).
Uppgifter
- Derivera genom att använda dig av produktregeln.
- \( (x-1)(x^2+1) \)
\( 2x(x-1)+1(x^2+1)=3x^2-2x+1 \)
- \( (-x^2+1)(2-x) \)
\( -(-x^2 +1) - 2x(2-x)=3x^2-4x-1 \)
- \( (x-1)(x^2+1) \)
- Bestäm
- \( D(x-2)(2-x) \)
\( -1(x - 2) +1(2-x)=-2x+4 \)
- \( D(2x^3-2x)(x^2+x) \)
\( (2x+1)(2x^3-2x)+(6x^2-2)(x^2+x)= 10x^4 + 8x^3 - 6x^2 - 4x \)
- \( D(x-1)(x+1) \)
\( (x-1)+(x+1)=2x \) eller via \( D(x^2-1)=2x \).
- \( D(x-2)(2-x) \)
- Bestäm \( D(x-2)^2 \).
\( D(x-2)(x-2)=1(x-2)+1(x-2)=2x-4 \) eller som \( D(x^2-4x+4)=2x-4 \).
- Bestäm \( D 2x(x+1) \)
Vi får \( D 2x(x+1) = 2(x+1) + 2x\cdot 1 = 2x +2 +2x = 4x+2\).
- Bestäm \( D x(x-1)(x+1) \).
Vi får \( D x(x-1)(x+1) = Dx(x^2-1) = 1(x^2-1)+x\cdot 2x = x^2-1+2x^2 = 3x^2 -1 \).
- Grafen av derivatafunktionen \( f'(x) \) ser du i bilden nedan.
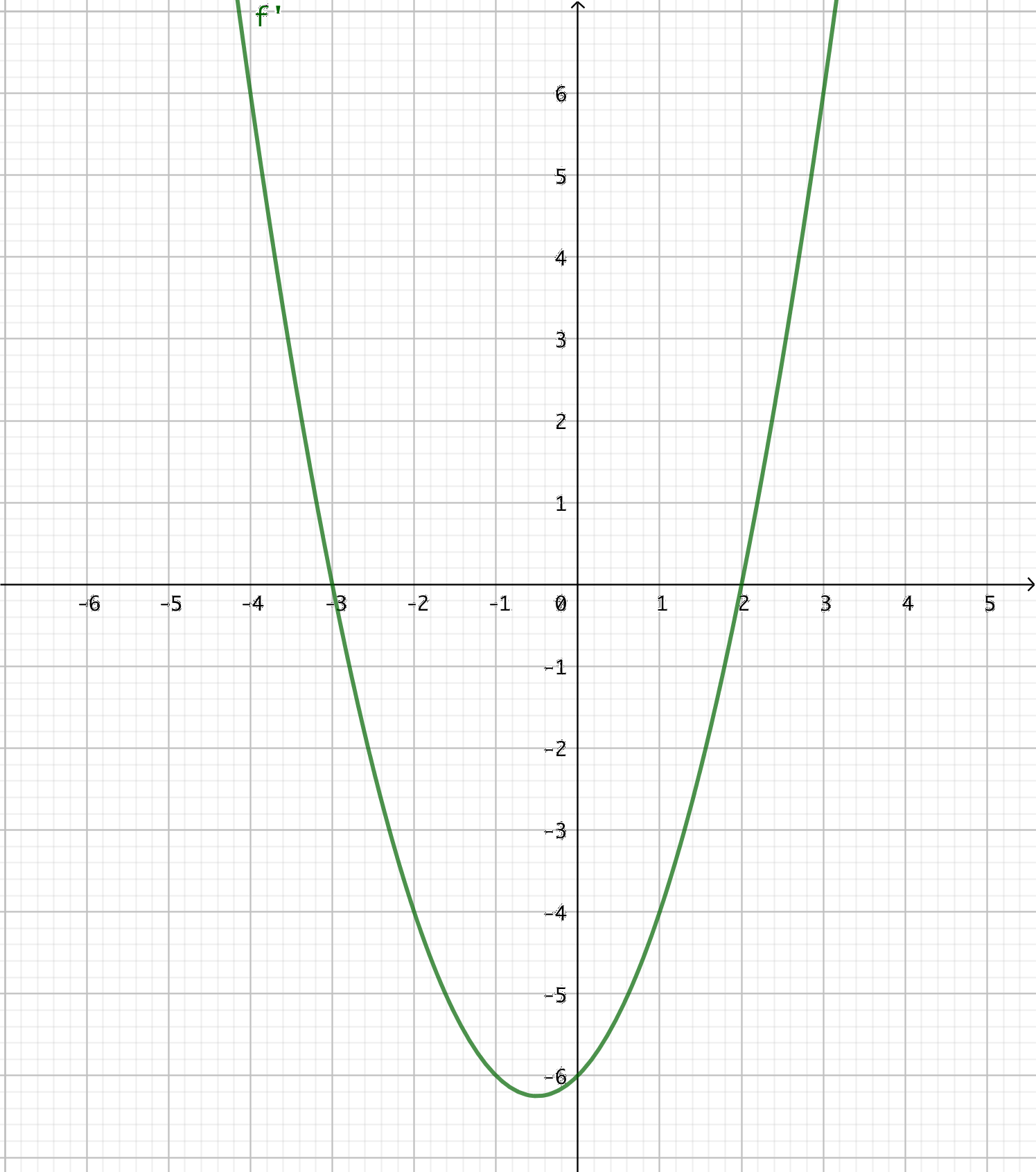
Vad kan du berätta om funktionen \( f \)?
Eftersom derivatafunktionen har nollställena \( x = -3 \) och \( x = 2 \) och går från positiv till negativ eller negativ till positiv byter funktionen \( f \) riktning där.
I intervallen \( x < -3 \) och \( x > 2 \) är \( f' \) positiv, då är \( f \) växande.
I intervallet \( -3 < x < 2 \) är \( f' \) negativ, då är \( f \) avtagande.
Eftersom \( f' \) är en parabel är \( f \) en tredjegradsfunktion.
- Grafen av derivatafunktionen \( f'(x) \) ser du i bilden nedan.

Vad kan du berätta om funktionen \( f \)?
Eftersom derivatafunktionen har nollstället \( x = 1 \) men alltid är positiv har \( f \) en terasspunkt där.
\( f' \) är positiv i alla punkter utom i \( x = 1 \). Alltså är \( f \) växande.
Med andra ord så har vi en strängt växande funktion som har en terasspunkt i \( x = 1 \).
Eftersom \( f' \) är en parabel är \( f \) minst en tredjegradsfunktion.
- Grafen av derivatafunktionen \( f'(x) \) ser du i bilden nedan.

Vad kan du berätta om funktionen \( f \)?
Derivatafunktionen har nollställena \( x = -2 \) och \( x = 0 \). Vid \( x = -2 \) går derivatafunktionen från positiv till negativ, där byter funktionen \( f \) riktning. Vid \( x = 0 \) är \( f' \) negativ, där har vi en terasspunkt. Vi har ett dubbelnollställe.
Då \( x < -2 \) är \( f' \) positiv, då är \( f \) växande.
I intervallet \( -2 < x < 0 \) och \( x > 0 \) är \( f' \) negativ, då är \( f \) avtagande.
Eftersom \( f' \) är av tredje grad är \( f \) minst en fjärdegradsfunktion.
- Bestäm minsta värde för funktionen \( f(x)=(x-1)(x+2) \).
\( f'(x)=1(x+2)+1(x-1)=2x+1 \) som har nollstället \( x=-\dfrac{1}{2} \). Eftersom vi har en parabel som öppnar sig uppåt hittar vi minsta stället i \( f(-\dfrac{1}{2})=(-\dfrac{1}{2}-1)(-\dfrac{1}{2}+2) = -\dfrac{9}{4} \).
- Bestäm extremvärden för funktionen \( f(x)=(x^2-x)(x-1) \).
Extrempunkterna är i \( x=\dfrac{1}{3} \) och \( x=1 \).
Då \( x=\dfrac{1}{3} \) har vi värdet \( f(\dfrac{1}{3})=\dfrac{4}{27} \).
Då \( x=1 \) har vi värdet \( f(1)=0 \).
Teckenschemat ger att funktionen växer, avtar och växer. Lokalt största värde i \( \dfrac{1}{3} \), värdet är \( \dfrac{4}{27} \). Lokalt minsta värde i \( 1 \), värdet är \( 0 \).
- Bestäm de punkter där \( f(x) = x(x+1)(x+2) \) byter riktning.
Antingen förenklar du till \( f(x) = (x^2+x)(x+2) \) eller till \( f(x) = x^3+3x^2+2x \) före du deriverar.
\( f'(x) = 3x^2+6x+2 \).
De punkter där funktionen byter riktning är derivatans nollställen, \( f'(x)=0 \). Alltså \( 3x^2 +6x+2 = 0 \). Punktern är \( x_1 = \dfrac{-3-\sqrt{3}}{3} \) och \( x_2 = \dfrac{-3+\sqrt{3}}{3} \).
- Bestäm \( f'(1) \) då \( f(x) = (x^3-4)(x^2+1) \).
Vi får \( f'(x) = 3x^2(x^2+1) + (x^3-4)\cdot 2x = 5x^4 + 3x^2-8x \).
\( f'(1) = 5\cdot 1^4 -3\cdot 1^2 -8 \cdot 1 = 0 \).
- Bestäm när funktinen \( f(x) = (x^2-2)(2x+1) \) är växande och avtagande.
Derivatafunktionen är \( f'(x) = 2x(2x+1)+(x^2-2)\cdot 2 = 6x^2+2x-4 \).
Derivatans nollställe, \( f'(x)=0 \), alltså \( 6x^2+2x-4 = 0 \) då \( x = -1 \) och \( x = \dfrac{2}{3} \).
Vi bildar ett teckenchema:
\( \begin{array}{c|ccccc} & & -1 & & \dfrac{2}{3} \\ \hline f'(x) & + & 0 & - & 0 & + \\ f(x) & \nearrow & & \searrow & & \nearrow \\ \end{array} \)
Vi har ett lokalt maximum i \( x = -1 \), \( f(-1) = 1 \).
Vi har ett lokalit minimum i \( x = \dfrac{2}{3} \), \( f(\dfrac{2}{3}) = -\dfrac{98}{27} \).