3. Uppgifter med rottermer

Diskutera med din bänkkamrat över följande

När är en kvadratrot definierad?
Hur förenklar vi kvadratrötter, tex $ \sqrt{3}\cdot \sqrt{6} $ eller $ 5\sqrt{2} - \sqrt{18} $ ?
Hur kvadrerar vi kvadratrötter, tex $ (4\sqrt{2})^2 $?
Hur deriverar vi en kvadratrot, tex $ D\sqrt{x^2-1} $?
Hur integrerar vi en kvadratrot, tex $ \displaystyle\int \sqrt{x^2-1} \mathrm{\,d}x $?

Inledande uppgifter

När är en kvadratrot definierad?

Då det vi tar roten av är större än 0.

När är följande kvadratrötter definierade?

Påstående	$ x \geq -2 $	$ x \geq -1 $	$ x \geq 0 $	$ x \geq 1 $	$ x \geq 2 $
$ \sqrt{x} $
$ \sqrt{x+1} $
$ \sqrt{x-1} $
$ \sqrt{x+2} $
$ \sqrt{x-2} $
$ \sqrt{\dfrac{x}{2}} $
$ \sqrt{\dfrac{x}{2}+1} $
$ \sqrt{\dfrac{x}{2}-1} $

Påstående	$ x \geq -2 $	$ x \geq -1 $	$ x \geq 0 $	$ x \geq 1 $	$ x \geq 2 $
$ \sqrt{x} $
$ \sqrt{x+1} $
$ \sqrt{x-1} $
$ \sqrt{x+2} $
$ \sqrt{x-2} $
$ \sqrt{\dfrac{x}{2}} $
$ \sqrt{\dfrac{x}{2}+1} $
$ \sqrt{\dfrac{x}{2}-1} $

Kombinera så att uttrycken har samma värde.

Välj av sex följande uttryck: $ \sqrt{2}\cdot \sqrt{5} $, $ \sqrt{2}\cdot \sqrt{8} $, $ \sqrt{3}\cdot \sqrt{5} $, $ \sqrt{3} \cdot \sqrt{6} $, $ \sqrt{8} $ och $ \sqrt{12} $

	$ 2\sqrt{2} $
	$ 3\sqrt{2} $
	$ \sqrt{10} $
	$ 4 $
	$ \sqrt{15} $
	$ 2\sqrt{3} $

$ \sqrt{8} $	$ 2\sqrt{2} $
$ \sqrt{3} \cdot \sqrt{6} $	$ 3\sqrt{2} $
$ \sqrt{2}\cdot \sqrt{5} $	$ \sqrt{10} $
$ \sqrt{2}\cdot \sqrt{8} $	$ 4 $
$ \sqrt{3}\cdot \sqrt{5} $	$ \sqrt{15} $
$ \sqrt{12} $	$ 2\sqrt{3} $

Kombinera rätt kvadrering med rätt värde.

Välj bland följande uttryck: $ (\sqrt{2})^2 $, $ (\sqrt{3})^2 $, $ (2\sqrt{2})^2 $, $ (2\sqrt{3})^2 $, $ (3\sqrt{2})^2 $ och $ (4\sqrt{2})^2 $.

	32
	8
	18
	2
	3
	12

$ (4\sqrt{2})^2 $	32
$ (2\sqrt{2})^2 $	8
$ (3\sqrt{2})^2 $	18
$ (\sqrt{2})^2 $	2
$ (\sqrt{3})^2 $	3
$ (2\sqrt{3})^2 $	12

Bestäm följande derivator
1. $ D \sqrt{x} $
  
  $ D \sqrt{x} = D x^{\frac{1}{2}} = \dfrac{1}{2}x^{\frac{1}{2}-1} = \dfrac{1}{2}x^{-\dfrac{1}{2}} = \dfrac{1}{2\sqrt{x}} $
2. $ D\sqrt{x^2-1} $
  
  $ D \sqrt{x^2-1} = D (x^2-1)^{\frac{1}{2}} = \dfrac{1}{2}(x^2-1)^{-\dfrac{1}{2}} \cdot 2x= \dfrac{x}{\sqrt{x^2-1}} $
3. $ D\sqrt{x^2+x} $
  
  $ D\sqrt{x^2+x} = D(x^2+x)^{\frac{1}{2}} = \dfrac{1}{2}(x^2+x)^{-\dfrac{1}{2}}\cdot(2x+1) = \dfrac{2x+1}{2\sqrt{x^2+x}} $
Bestäm följande integraler
1. $ \displaystyle\int \sqrt{x} \mathrm{\,d}x $
  
  $ \displaystyle\int \sqrt{x} \mathrm{\,d}x = \displaystyle\int x^{\frac{1}{2}} \mathrm{\,d}x = \dfrac{1}{1+\dfrac{1}{2}}x^{1+\dfrac{1}{2}} + C= \dfrac{1}{\dfrac{3}{2}}x^{\frac{3}{2}}+C = \dfrac{2x\sqrt{x}}{3}+C $
2. $ \displaystyle\int \sqrt{x+1}\mathrm{\,d}x $
  
  $ \displaystyle\int \sqrt{x+1}\mathrm{\,d}x = \displaystyle\int (x+1)^{\frac{1}{2}} = \dfrac{1}{\dfrac{3}{2}}(x+1)^{\frac{3}{2}}+C = \dfrac{2(x+1)\sqrt{x+1}}{3}+C $
  Eftersom den inre funktionens, $ x+1 $, derivata är $ 1 $ behöver vi inte beakta den.
3. $ \displaystyle\int x\sqrt{x^2+1} \mathrm{\,d}x $
  
  $ \displaystyle\int x\sqrt{x^2+1} \mathrm{\,d}x = \displaystyle\int x(x^2+1)^{\frac{1}{2}}\mathrm{\,d}x = \dfrac{1}{2}\displaystyle\int 2x(x^2+1)^{\frac{1}{2}} \mathrm{\,d}x = \dfrac{1}{2}\cdot\dfrac{1}{\dfrac{3}{2}}(x^2+1)^{\frac{3}{2}}+C = \dfrac{1}{3}(x^2+1)\sqrt{x^2+1}+C $

Utan räknare

Exempel 1 Visa utan användning av närmevärden att $ x $ och $ y $ är inverterade tal om $ x=\sqrt{5-2\sqrt{6}} $ och $ y=\sqrt{2\sqrt{6}+5} $.

Lösning

Om $ x $ och $ y $ är inverterade tal gäller att $ x \cdot y = 1 $. Alltså

$ \begin{array}{l} \sqrt{5-2\sqrt{6}} \cdot \sqrt{2\sqrt{6}+5} \\ = \sqrt{(5-2\sqrt{6})(2\sqrt{6}+5)} \\ = \sqrt{10\sqrt{6}+25-4\sqrt{36}-10\sqrt{6}} \\ = \sqrt{25-4\cdot6} \\ = \sqrt{25-24} \\ = \sqrt{1} = 1 \\ \end{array} $

Alltså: $ x $ och $ y $ är varandras inverterade tal.

Exempel 2 Visa utan att använda närmevärden att $ \sqrt{85-60\sqrt{2}}=3\sqrt{5}-2\sqrt{10} $.

Lösning

För en kvadratrot gäller $ \sqrt{a} = b \Leftrightarrow b^2=a $ och $ a,b \geq 0 $. Vi betecknar $ a=85-60\sqrt{2} $ och $ b=3\sqrt{5}-2\sqrt{10} $. $ b=3\sqrt{5}-2\sqrt{10} \geq 0 $ så vi börjar räkna.

$ b^2 = (3\sqrt{5}-2\sqrt{10})^2 = 9\cdot 5 -12\sqrt{50}+4\cdot 10 = 85 -12\cdot5\sqrt{2} = 85-60\sqrt{2} = a $.

Alltså $ \sqrt{85-60\sqrt{2}}=3\sqrt{5}-2\sqrt{10} $.

Exempel 3 Lös olikheten $ \mid x-1 \mid - \sqrt{x+1} > 0 $.

Lösning

Kvadratroten ger att $ x+1\geq 0 \Leftrightarrow x\geq -1 $.

$ \begin{array}{rrcll} & \mid x-1 \mid - \sqrt{x+1} & > & 0 & \\ & \mid x-1 \mid & > & \sqrt{x+1} & \mid ()^2 \textrm{eftersom bägge led positiva} \\ & (x-1)^2 & > & x+1 & \\ & x^2-2x+1 & > & x+1 & \\ & x^2 -3x & > & 0 & \\ \textrm{Löser ekvation: } & x^2-3x & = & 0 & \\ & x(x-3) & = & 0 & \\ \textrm{Alltså } & x=0 & \textrm{eller} & x-3=0 \\ & & & x=3 \\ \end{array} $

Vi har en parabel som öppnar sig uppåt med nollställena 0 och 3.

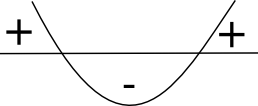
Och när vi jämför med när roten är definierad får vi svaret $ -1\leq x \leq 0 $ eller $ x\geq 3 $.

Exempel 4 Lös ekvationen $ x-\sqrt{43-3x}=11 $.

Lösning

Roten är definierad då $ 43-3x \geq 0 \Leftrightarrow x \leq \dfrac{43}{3} = 14\dfrac{1}{3} $.

$ \begin{array}{rrcll} & x-\sqrt{43-3x} & = & 11 & \\ & -\sqrt{43-3x} & = & 11-x & \mid (\quad)^2 \text{ då } x-11 \geq 0 \Leftrightarrow x \geq 11 \\ & 43-3x & = & 121-22x+x^2 & \\ & x^2-19x +78 & = & 0 & \\ & x & = & \dfrac{19\pm \sqrt{(-19)^2-4\cdot 1\cdot 78}}{2\cdot 1} & \\ & & = & \dfrac{19\pm\sqrt{49}}{2}=\dfrac{19\pm 7}{2} & \\ \end{array} $

Rötterna är $ x=\dfrac{19-7}{2}=6 $ och $ x=\dfrac{19+7}{2}=13 $.

Alltså $ x= 13 $.

Derivera funktionen $ f(x) = 2\sqrt{x} + \dfrac{3}{x^2} - 4 $. [V06, 2a)]

$ f(x) = 2\sqrt{x} + \dfrac{3}{x^2} - 4 = 2 x^{\frac{1}{2}} + 3 x^{-2} $.

$ f'(x)=x^{-\dfrac{1}{2}}-6x^{-3} (= \dfrac{1}{\sqrt{x}} + \dfrac{6}{x^3}) $
Lös ekvationen $ \sqrt{x-2} = 1+ \dfrac{2}{\sqrt{x-2}} $. [H00, 2]

$ \begin{array}{rcll} \sqrt{x-2} & = & 1+ \dfrac{2}{\sqrt{x-2}} & \mid \sqrt{x-2}\\ (\sqrt{x-2})^2 & = & \sqrt{x-2} + \sqrt{x-2}\cdot \dfrac{2}{\sqrt{x-2}} \\ x-2 & = & \sqrt{x-2} +2 \\ x-4 & = & \sqrt{x-2} & \mid (\quad)^2 \\ x^2-8x+16 & = & x-2 \\ x^2-9x +18 & = & 0\\ x & = & \dfrac{9\pm \sqrt{(-9)^2-4\cdot 1 \cdot 18}}{2\cdot 1} \\ x & = & \dfrac{9\pm3}{2} \end{array} $
Vi får rötterna $ x=3 $ och $ x=6 $.

Kontroll ger att $ x=6 $.
Bestäm de reella rötterna till ekvationen $ \sqrt{2-x} = x+2 $. [H08, 7]

$ \begin{array}{rcll} \sqrt{2-x} & = & x+2 & \mid (\quad)^2 \\ 2-x & = & (x+2)^2 \\ 2-x & = & x^2+4x+4 \\ x^2 +5x -2 & = & 0 \\ \text{Rotformeln ger} \\ x & = & \dfrac{-5\pm\sqrt{17}}{2} \\ \end{array} $
Eftersom vi har kvadrerat måste rötterna vara positiva, alltså $ x=\dfrac{-5+\sqrt{17}}{2} $.
Visa att värdena av uttrycken $ x^2 +1 + \sqrt{x^4+2x^2} $ och $ x^2+1 -\sqrt{x^4 + 2x^2} $ är varandras inverterade tal för alla värden på $ x $. [V88, 2]

Om $ x $ och $ y $ är varandras inverterade tal gäller att $ x\cdot y =1 $.

$ \begin{array}{rcl} x \cdot y & = & (x^2+1+\sqrt{x^4+2x^2}) (x^2+1-\sqrt{x^4+2x^2}) \\ & = & (x^2+1)^2-(\sqrt{x^4 + 2x^2})^2\\ & = & x^4 + 2x^2 +1 -x^4-2x^2 \\ & = & 1\\ \end{array} $

Med räknare

Exempel 1 Bestäm största och minsta värdet för uttrycket $ 2x-\sqrt{1-x^2} $ [V92, 7]

Lösning

TI nSpire CAS

Vi definierar funktionen på räknaren, define f(x)=2x- sqrt(1-x^2).

Funktionen är definierad då $ 1-x^2 \geq 0 \Leftrightarrow -1\leq x \leq 1 $. På räknaren solve()

Derivera funktionen och spara derivatafunktionen som $ g(x) $, define g(x)=$ \dfrac{d}{dx} f(x) $.

Bestäm nollställena för derivatan, solve(g(x)=0,x). Nollstället är $ x=\dfrac{-2\sqrt{5}}{5} $.

Funktionen får sitt största och minsta värde i derivatans nollställe eller i intervallets ändpunkter.

$ f(-1)= -2 $

$ f(\dfrac{-2\sqrt{5}}{5}) = -\sqrt{5} \approx -2,24 $.

$ f(1)=2 $

Minsta värdet är $ -\sqrt{5} $ och största värdet 2.

Exempel 2 En rektangel har en sida på x-axeln och två hörn på cirkeln $ x^2+y^2=2 $ ovanför $ x $-axeln. Bestäm rektangelns största möjliga area.

Lösning

TI nSpire CAS

För att rita funktionerna på räknaren löser vi $ x^2 + y^2 =2 $ som $ y = \pm\sqrt{2-x^2} $. Övre delen av cirkeln får vi genom att rita $ y=\sqrt{2-x^2} $ och cirkelns nedre del genom att rita $ y=-\sqrt{2-x^2} $.

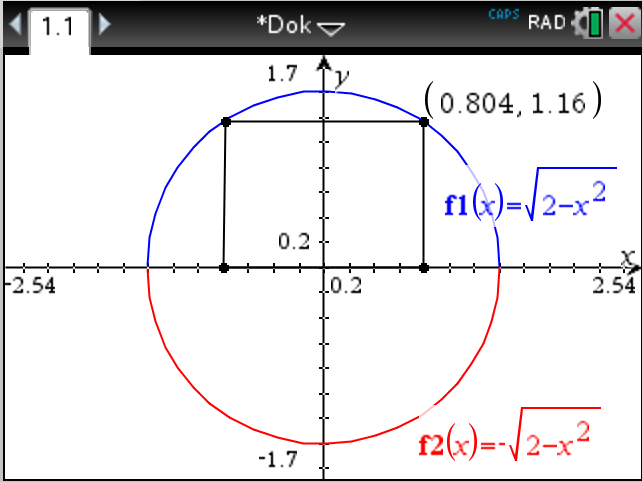
Rektangelns $ x $ koordinat är $ x $. $ y $-koordinaten är $ \sqrt{2-x^2} $. $ x $ rör sig mellan $ 0 $ och $ 2 $.

Arean för kvadraten är $ A(x)=2x \cdot \sqrt{2-x^2} $. Vi definierar den via define kommandot.

Vi bestämmer derivatan och derivatans nollställen.

Derivatans nollställe i intervallet $ [0,2] $ är $ x=1 $.

Vi hittar största och minsta värde i derivatans nollställe eller i intervallets ändpunkter.

Största möjliga arean är 2.

Exempel 3 Kurvan $ y^2=x^2-x^4, x\geq 0 $ begränsar ett slutet område. Beräkna områdets area. Beräkna ytterligare volymen av den rotationskropp som uppstår, då området roterar kring $ x $-axeln.

Lösning

Ti nSpire CAS

Vi skriver kurvan som $ y = \pm \sqrt{x^2-x^4} $ och plottar in bägge leden.

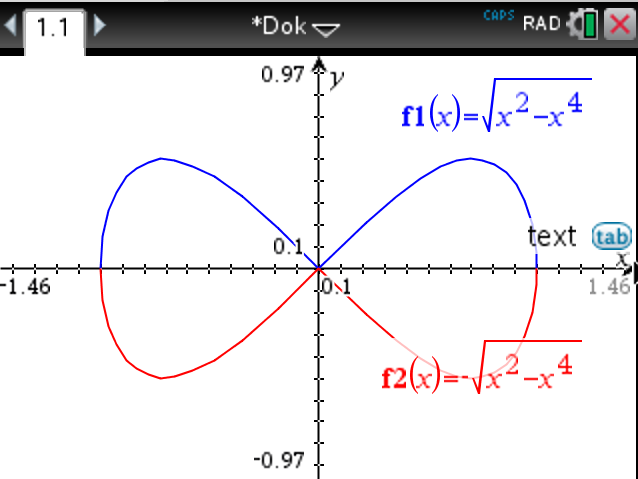
Vi behöver skärningspunkterna. För att räkna dem definierar vi funktionen. Vi tar endast den övre eftersom figuren är symmetrisk.

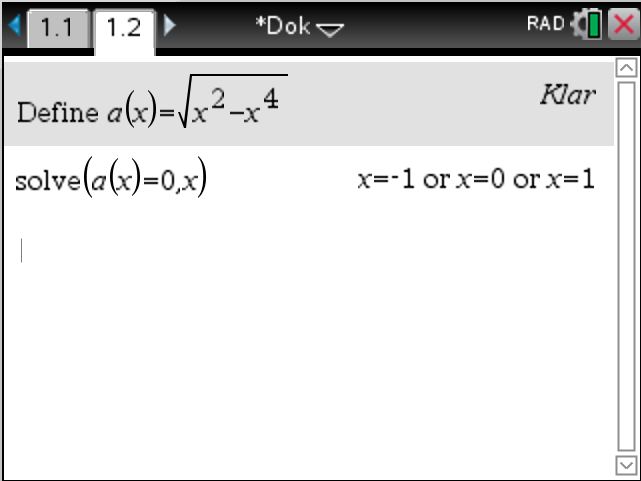
Våra intressanta nollställen är $ x=0 $ och $ x=1 $.

Arean får vi som $ \dfrac{2}{3} $. Volymen som $ \dfrac{2\pi}{15} $.

Beräkna arean av det område som begränsas av de räta linjerna $ x=0, x=2, y=0 $ och kurvan $ y=\dfrac{3x}{\sqrt{2x^2+1}} $. [V84, 6]

Vi skall bestämma $ A = \displaystyle\int_0^2 \dfrac{3x}{\sqrt{2x^2+1}} \mathrm{\,d}x = 3 $.
Bestäm funktionens $ f(x)=x+\sqrt{9-x^2}, -3\leq x \leq 3 $ största och minsta värde. Rita funktionens graf. [V08, 9]

$ f(x)= x+\sqrt{9-x^2} = x+(9-x^2)^{\frac{1}{2}} $.

$ f'(x)=1 -2x\cdot \dfrac{1}{2}(9-x^2)^{-\dfrac{1}{2}} = 1-\dfrac{x}{\sqrt{9-x^2}} $.

Söker nollstället, $ f'(x)=0 $, alltså

$ \begin{array}{rcll} 1-\dfrac{x}{\sqrt{9-x^2}} & = & 0 \\ \\ \dfrac{x}{\sqrt{9-x^2}} & = & 1 \\ \\ \sqrt{9-x^2} & = & x & \mid (\quad)^2\\ 9-x^2 & = & x^2 \\ 2x^2 & = & 9 \\ x^2 & = & \dfrac{9}{2} & \mid{\sqrt{\quad}} \\ x & = & \pm \dfrac{3}{\sqrt{2}}\\ \end{array} $

Roten är $x=\dfrac{3}{\sqrt{2}}.

Största och minsta värdet får vi i derivatans nollställe eller i intervallets ändpunkter.

$ \begin{array}{rcl} f(-3) & = & -3 +\sqrt{9-(-3)^2} = -3\\ \\ f(\dfrac{3}{\sqrt{2}}) & = & \dfrac{3}{\sqrt{2}} +\sqrt{9-(\dfrac{3}{\sqrt{2}})^2} = \dfrac{3}{\sqrt{2}} +\sqrt{9-\dfrac{9}{2}} = \dfrac{3}{\sqrt{2}} +\sqrt{\dfrac{18-9}{2}} = \dfrac{3}{\sqrt{2}} + \dfrac{3}{\sqrt{2}} = 3\sqrt{2}\\ \\ f(3) & = & 3 +\sqrt{9-3^2} = 3\\ \end{array} $

Största värdet är $ 3\sqrt{2} $ och minsta värdet är $ -3 $.

Påstående	\( x \geq -2 \)	\( x \geq -1 \)	\( x \geq 0 \)	\( x \geq 1 \)	\( x \geq 2 \)
\( \sqrt{x} \)
\( \sqrt{x+1} \)
\( \sqrt{x-1} \)
\( \sqrt{x+2} \)
\( \sqrt{x-2} \)
\( \sqrt{\dfrac{x}{2}} \)
\( \sqrt{\dfrac{x}{2}+1} \)
\( \sqrt{\dfrac{x}{2}-1} \)

Påstående	\( x \geq -2 \)	\( x \geq -1 \)	\( x \geq 0 \)	\( x \geq 1 \)	\( x \geq 2 \)
\( \sqrt{x} \)
\( \sqrt{x+1} \)
\( \sqrt{x-1} \)
\( \sqrt{x+2} \)
\( \sqrt{x-2} \)
\( \sqrt{\dfrac{x}{2}} \)
\( \sqrt{\dfrac{x}{2}+1} \)
\( \sqrt{\dfrac{x}{2}-1} \)

	\( 2\sqrt{2} \)
	\( 3\sqrt{2} \)
	\( \sqrt{10} \)
	\( 4 \)
	\( \sqrt{15} \)
	\( 2\sqrt{3} \)

\( \sqrt{8} \)	\( 2\sqrt{2} \)
\( \sqrt{3} \cdot \sqrt{6} \)	\( 3\sqrt{2} \)
\( \sqrt{2}\cdot \sqrt{5} \)	\( \sqrt{10} \)
\( \sqrt{2}\cdot \sqrt{8} \)	\( 4 \)
\( \sqrt{3}\cdot \sqrt{5} \)	\( \sqrt{15} \)
\( \sqrt{12} \)	\( 2\sqrt{3} \)

\( (4\sqrt{2})^2 \)	32
\( (2\sqrt{2})^2 \)	8
\( (3\sqrt{2})^2 \)	18
\( (\sqrt{2})^2 \)	2
\( (\sqrt{3})^2 \)	3
\( (2\sqrt{3})^2 \)	12