15. Repetition
Sedan är det bara att repetera.
Uppgifter
- Längden av bågen i en sektor är 8,0 m och radien är 2,0 m. Hur stor är sektorvinkeln i radianer och grader?
Som radianer: \( \alpha = \dfrac{8 \text{ m}}{2 \text{ m}} = 4 \) radianer.
Som grader: \( \dfrac{x}{180^{\circ}} = \dfrac{4 \text{ rad}}{\pi \text{ rad}} \) ger \( \alpha = 229,2^{\circ} \).
- Storleken av en sektorvinkel är \( \dfrac{5\pi}{4} \) och längden av bågen är \( 75\pi \). Bestäm längden av radien.
Eftersom \( \alpha =\dfrac{b}{r} \) får vi \( \dfrac{5\pi}{4} = \dfrac{75\pi}}{r} \).
Alltså \( r = 60 \).
- Förenkla följande uttryck utan räknare.
- \( \dfrac{\sin 20^{\circ}}{\cos 70^{\circ}} \)
Vi får
\( \begin{array}{rcl} \dfrac{\sin 20^{\circ}}{\cos 70^{\circ}} & = & \dfrac{\cos(90^{\circ} - 20^{\circ})}{\cos 70^{\circ}} \\ & = & \dfrac{\cos 70^{\circ}}{\cos 70^{\circ}} \\ & = & 1 \\ \end{array} \)
- \( \dfrac{\cos \frac{\pi}{5}}{\sin \frac{13\pi}{10}} \)
Vi får
\( \begin{array}{rcl} \dfrac{\cos \frac{\pi}{5}}{\sin \frac{13\pi}{10}} & = & \dfrac{\cos \frac{\pi}{5}}{\sin \frac{10\pi + 3\pi}{10}} \\ & = & \dfrac{\cos \frac{\pi}{5}}{\sin (\pi +\frac{3\pi}{10})} \\ & = & \dfrac{\cos \frac{\pi}{5}}{\sin (\pi -(-\frac{3\pi}{10}))} \\ & = & \dfrac{\cos \frac{\pi}{5}}{\sin (-\frac{3\pi}{10})} \\ & = & \dfrac{\cos \frac{\pi}{5}}{-\sin \frac{3\pi}{10}} \\ & = & \dfrac{\cos \frac{\pi}{5}}{-\cos(\frac{\pi}{2} - \frac{3\pi}{10})} \\ & = & \dfrac{\cos \frac{\pi}{5}}{-\cos \frac{2\pi}{10}} \\ & = & \dfrac{\cos \frac{\pi}{5}}{-\cos \frac{\pi}{5}} \\ & = & -1 \\ \end{array} \)
- \( \dfrac{\sin 20^{\circ}}{\cos 70^{\circ}} \)
- Lös följande ekvationer. Svara som grader.
- \( \sin x = 0,43 \)
Räknaren ger oss en lösning, \( 25,5^{\circ} \).
Alltså \( 25,5^{\circ} + n\cdot 360^{\circ} \).Eftersom sinus är y-koordinaten i enhetscikeln får vi den andra vinkeln som.
Den andra är \( 180^{\circ} - 25,5^{\circ} = 154,5^{\circ} + n \cdot 360^{\circ} \).
- \( \cos x = 0,76 \)
Räknaren ger oss en lösning, \( 40,5^{\circ} \).
Eftersom cosiuns är x-koordinaten i enhetscirkeln får vi den andra vinkeln som.
Alla vinklar är \( \pm 40,5^{\circ} + n\cdot 360^{\circ} \).
- \( \tan x = 0,11 \)
Räknaren ger oss en lösning, \( 6,3^{\circ} \).
Alla vinklar är \( 6,3^{\circ} + n \cdot 180^{\circ} \).
- \( \sin x = 0,43 \)
- Bestäm värdet av \( \sin 3\alpha + \cos 2 \alpha \) då
- \( \alpha = 90^{\circ} \)
Vi har \( \sin 3\alpha + \cos 2 \alpha = \sin 270^{\circ} + \cos 180^{\circ} = -1 -1 = -2 \).
- \( \alpha = -90^{\circ} \)
Vi har \( \sin 3\alpha + \cos 2 \alpha = \sin (-270^{\circ}) + \cos (-180^{\circ}) = 1 -1 = 0 \).
- \( \alpha = 90^{\circ} \)
- Bestäm värdet av \( \sin 3\alpha + 3\cos \alpha \) då
- \( \alpha = 45^{\circ} \)
Vi har \( \sin 3\alpha + 3\cos \alpha = \sin 135^{\circ} + 3\cos 45^{\circ} = \dfrac{1}{\sqrt{2}} +3\cdot\dfrac{1}{\sqrt{2}} = 2\sqrt{2} \).
- \( \alpha = 135^{\circ} \)
Vi har \( \sin 3\alpha + 3\cos \alpha = \sin 405^{\circ} + 3\cos 135^{\circ} = \sin 45^{\circ} + 3\cos 135^{\circ} = \dfrac{1}{\sqrt{2}} +3(-\dfrac{1}{\sqrt{2}}) = -\sqrt{2} \).
- \( \alpha = 45^{\circ} \)
- Vi vet att \( \cos x = \dfrac{4}{5} \) och att \( 270^{\circ} < x < 360^{\circ} \). Bestäm de exakta värdena för \( \sin x \) och \( \tan x \).
Eftersom vi är i fjärde kvadraten är sinus och tangens negativa.
Vi får \( \sin x = -\sqrt{1-\cos^2 x} = -\sqrt{1-(\dfrac{4}{5})^2} = -\dfrac{3}{5} \).
Vidare \( \tan x = \dfrac{\sin x}{\cos x} = -\dfrac{3}{4} \).
Eller så utnyttjar vi Pythagoras. Längden av motstående katet är \( \sqrt{5^2-4^2} = 3 \). Den längden utnyttjar vi för att bilda sinus och tangens.
- Vi vet att \( \sin x = -\dfrac{1}{\sqrt{5}} \) och att \( 180^{\circ} < x < 270^{\circ} \). Bestäm de exakta värdena för \( \cos x \) och \( \tan x \). [V05, 2]
Eftersom vi är i tredje kvadraten är sinus och cosinus negativa.
Vi får \( \cos x = -\sqrt{1-\sin^2 x} = -\sqrt{1-(-\dfrac{1}{\sqrt{5}})^2} = -\dfrac{2}{\sqrt{5}} \).
Vidare \( \tan x = \dfrac{\sin x}{\cos x} = \dfrac{1}{2} \).
- Förenkla följande uttryck \( \dfrac{1-\cos^2 \alpha}{\sin\alpha \cdot \cos \alpha} \).
Vi får
\( \begin{array}{rcll} \dfrac{1-\cos^2 \alpha}{\sin\alpha \cdot \cos \alpha} & = & \dfrac{\sin^2 \alpha}{\sin\alpha \cdot \cos \alpha} \\ & = & \dfrac{\sin \alpha}{\cos \alpha} \\ & = & \tan \alpha \\ \end{array} \)
- Lös följande ekvationer. Räkna i radianer.
- \( 2\sin(\dfrac{\pi}{3}-x) + \sqrt{3} = 0 \)
Vi får
\( \begin{array}{rcl} 2\sin(\dfrac{\pi}{3}-x) + \sqrt{3} & = & 0 \\ 2\sin(\dfrac{\pi}{3}-x) & = & - \sqrt{3} \\ \sin(\dfrac{\pi}{3}-x) & = & - \dfrac{\sqrt{3}}{2} \\ \dfrac{\pi}{3}-x & = & \dfrac{4\pi}{3} + n\cdot 2\pi \\ x & = & \pi + n\cdot 2\pi \\ \end{array} \)
och
\( \begin{array}{rcl} \dfrac{\pi}{3}-x & = & \pi - \dfrac{4\pi}{3} + n\cdot 2\pi \\ x & = & \dfrac{2\pi}{3} + n\cdot 2\pi \\ \end{array} \)
- \( \tan(2x-\dfrac{\pi}{6}) = -1 \)
Definitionsmängden: \( 2x -\dfrac{\pi}{6} \not= \dfrac{\pi}{2} +n\pi \). Alltså då \( x \not= \dfrac{\pi}{3} +n\dfrac{\pi}{2} \)
Vi får
\( \begin{array}{rcl} 2x-\dfrac{\pi}{6} & = & \dfrac{3\pi}{4} +n\pi \\ 2x & = & \dfrac{11\pi}{12} +n\pi \\ x & = & \dfrac{11\pi}{24} +n\dfrac{\pi}{2} \\ \end{array} \)
- \( 2\sin(\dfrac{\pi}{3}-x) + \sqrt{3} = 0 \)
- Lös följande ekvationer. Räkna i radianer.
- \( \sin(2x - \dfrac{\pi}{2}) = \sin x \)
Vi får
\( \begin{array}{rcl} 2x - \dfrac{\pi}{2} & = & x + n\cdot 2\pi \\ x & = & \dfrac{\pi}{2} + n\cdot 2\pi \\ \end{array} \)
och
\( \begin{array}{rcl} 2x - \dfrac{\pi}{2} & = & \pi - x + n\cdot 2\pi \\ 3x & = & \dfrac{3\pi}{2} + n\cdot 2\pi \\ x & = & \dfrac{\pi}{2} + n\cdot \dfrac{2\pi}{3} \\ \end{array} \)
- \( \tan 2x = \tan (\dfrac{\pi}{2}-x) \)
Först måste vi undersöka definitionsmängden.
\( \begin{array}{rcl} 2x & \not= & \dfrac{\pi}{2} + n \cdot \pi \\ x & \not= & \dfrac{\pi}{4} + n \cdot \dfrac{\pi}{2} \\ \end{array} \)
och
\( \begin{array}{rcl} \dfrac{\pi}{2}-x & \not= & \dfrac{\pi}{2} + n \cdot \pi \\ -x & \not= & + n \cdot \pi \\ x & \not= & + n \cdot \pi \\ \end{array} \)
Vi får
\( \begin{array}{rcl} 2x & = & \dfrac{\pi}{2}-x + n\cdot \pi \\ 3x & = & \dfrac{\pi}{2} + n\cdot \pi \\ x & = & \dfrac{\pi}{6} + n\cdot \dfrac{\pi}{3} \\ \end{array} \)
- \( \sin x \cos x + \cos x = 0 \)
Vi får
\( \begin{array}{rcl} \sin x \cos x + \cos x & = & 0 \\ \cos x (\sin x + 1) & = & 0 \\ \end{array} \)
Alltså \( cos x = 0 \). Det sker då \( x = \dfrac{\pi}{2} + n\pi \).
Och \( \sin x + 1 = 0\). Alltså \( \sin x = -1 \). Det sker då \( x = \dfrac{\pi}{2} + n\cdot 2\pi \).
- \( 2\cos^2 x + 3\cos x + 1 = 0 \)
Vi substituerar \( \cos x = t \).
Då är vår ekvation \( 2t^2+3t+1 = 0 \). Ekvationen har lösningarna \( t_1 = -\dfrac{1}{2} \) och \( t_2 = -1 \).
Vi substituerar tillbaka, \( \cos x = -\dfrac{1}{2} \) har lösningarna \( \dfrac{2\pi}{3} + n \cdot 2\pi \) och \( \dfrac{4\pi}{3} + n \cdot 2\pi \).
Dessutom får vi \( \cos x = -1 \) som har lösningarna \( \pi +n \cdot 2\pi \).
- \( \sin(2x - \dfrac{\pi}{2}) = \sin x \)
- Derivera följande funktioner.
- \( f(x) = (-3x^2+x)^4 \)
Vi har en sammansatt funktion.
Den yttre funktionen är \( x^4 \). Derivatan är \( 4x^3 \).
Den inre funktionen är \( -3x^2+x \). Derivatan är \( -6x+1 \)
Vi får \( f'(x) = 4(-3x^2+x)^3 \cdot (-6x+1) \).
- \( g(x) = \sin(3x^2) \)
Vi har en sammansatt funktion.
Den yttre funktionen är \( \sin x \). Derivatan är \( \cos x \).
Den inre funktionen är \( 3x^2 \). Derivatan är \( 6x \)
Vi får \( g'(x) = \cos(3x^2)\cdot 6x = 6x\cos(3x^2) \).
- \( h(x) = \cos^4 x \)
Vi har en sammansatt funktion.
Den yttre funktionen är \( x^4 \). Derivatan är \( 4x^3 \).
Den inre funktionen är \( \cos x \). Derivatan är \( -\sin x \)
Vi får \( h'(x) = 4 \cos^3 x).
- \( f(x) = (-3x^2+x)^4 \)
- Derivera följande funktioner.
- \( f(x) = 2x^4(x^2+2)^3 \)
Vi har en produkt av två funktioner där den ena är en sammansatt funktion.
Vi får först \( f'(x) = D2x^4 \cdot (x^2+2)^3 + 2x^4 \cdot D(x^2+2)^3 \).
Den andra delen är en sammansatt funktion.
Den yttre funktionen är \( x^3 \). Derivatan är \( 3x^2 \).
Den inre funktionen är \( x^2+2 \). Derivatan är \( 2x \)
Vi får
\( \begin{array}{rcl} f'(x) & = & 8x \cdot (x^2+2)^3 + 2x^4 \cdot 3(x^2+2)^2 \cdot 2x \\ & = & 8x(x^2+2)^3 + 24x^5 (x^2+2)^2 \\ & = & 8x[(x^2+2)^3 + 3x^4 (x^2+2)^2] \\ & = & 8x(x^2+2)^2[(x^2+2) + 3x^4] \\ & = & 8x(x^2+2)^2(3x^4 + x^2+2) \\ \end{array} \)
- \( g(x) = \dfrac{(2x+1)^6}{x^2+1} \)
Vi har en rationell funktion där täljaren är en sammansatt funktion.
Vi får först \( g'(x) = \dfrac{D(2x+1)^6(x^2+1)-(2x+1)^6\cdot D(x^2+1)}{(x^2+1)^2} \).
Det vi ursprungligen har i täljaren är en sammanstatt funktion.
Den yttre funktionen är \( x^6 \). Derivatan är \( 6x^5 \).
Den inre funktionen är \( 2x+1 \). Derivatan är \( 2 \)
Vi får
\( \begin{array}{rcl} g'(x) & = & \dfrac{6(2x+1)^5\cdot 2 \cdot (x^2+1)-(2x+1)^6\cdot (2x)}{(x^2+1)^2} \\ & = & \dfrac{(2x+1)^5[ 12 \cdot (x^2+1)-(2x+1)\cdot (2x)]}{(x^2+1)^2} \\ & = & \dfrac{(2x+1)^5( 8x^2 -2x +12)}{(x^2+1)^2} \\ \end{array} \)
Man kan också derivera funktionen genom att tänka den som \( g(x) = (2x+1)^6(x^2+1)^{-1} \).
- \( h(x) = \cos^2 (\sin x) \)
Vi har en sammansatt funktion.
Vi får
\( \begin{array}{rcl} h'(x) & = & 2\cos(\sin x) \cdot D (\cos (\sin x)) \\ & = & 2\cos(\sin x) \cdot (-\sin (\sin x)) \cdot \cos x \\ & = & -2\cos(\sin x) \cdot \sin (\sin x) \cdot \cos x \\ \end{array} \)
- \( f(x) = 2x^4(x^2+2)^3 \)
- Bestäm \( f^{(21)}(x) \) då
- \( f(x) = \sin x \)
Vi märker att
\( \begin{array}{rcl} f'(x) & = & \cos x \\ f''(x) & = & -\sin x \\ f^{(3)}(x) & = & -\cos x \\ f^{(4)}(x) & = & \sin x \\ f^{(5)}(x) & = & \cos x \\ f^{(6)}(x) & = & -\sin x \\ \vdots \\ \end{array} \)
Alltså är \( f'^{(21)}(x) = \cos x \).
- \( f(x) = \cos x \)
Vi märker att
\( \begin{array}{rcl} f'(x) & = & -\sin x \\ f''(x) & = & -\cos x \\ f^{(3)}(x) & = & \sin x \\ f^{(4)}(x) & = & \cos x \\ f^{(5)}(x) & = & -\sin x \\ f^{(6)}(x) & = & -\cos x \\ \vdots \\ \end{array} \)
Alltså är \( f'^{(21)}(x) = -\sin x \).
- \( f(x) = \sin x \)
- Låt \( f(x) = 5-3\cos x \). Bestäm största och minsta värde för funktionen.
För cosinus gäller att \( -1 \leq \cos x \leq 1 \).
Då gäller att \( -3 \leq 3\cos x \leq 3 \).
Och att \( -3 \leq -3\cos x \leq 3 \).
Alltså gäller att \( 2 \leq 5-3\cos x \leq 8 \).
Minsta värdet är 2 och största värdet är 8.
- Låt \( f(x) = 3+2\sin \dfrac{x}{2} \). Bestäm största och minsta värde för funktionen.
För sinus gäller att \( -1 \leq \sin x \leq 1 \).
Då gäller att \( -1 \leq \sin \dfrac{x}{2} \leq 1 \).
Och att \( -2 \leq 2\sin \dfrac{x}{2} \leq 2 \).
Alltså gäller att \( 1 \leq 3+2\sin \dfrac{x}{2} \leq 5 \).
Minsta värdet är 1 och största värdet är 5.
- Låt \( f(x) = -1+3\tan 2x \). Bestäm största och minsta värde för funktionen.
För tangens gäller att värdemängden är alla reella tal. Då är det ingen skillnad om vi multiplicerar med 3 eller subraherar med 1.
Största värdet är (plus) oändligheten, \( \infty \), minsta värdet är minus oändligheten, \( -\infty \).
- Temperaturen i celciusgrader på en semesterort under en dag följer funktionen \[ f(t) = 9,5\sin(0,262t-1,703) + 28,5 \] där \( t \) är antalet timmar som förflutit efter midnatt.
- Med vilken hastighet förändrades temperaturen kl 9.30?
Vi behöver derivatan, och i derivatafunktionen sätter vi in 9,5.
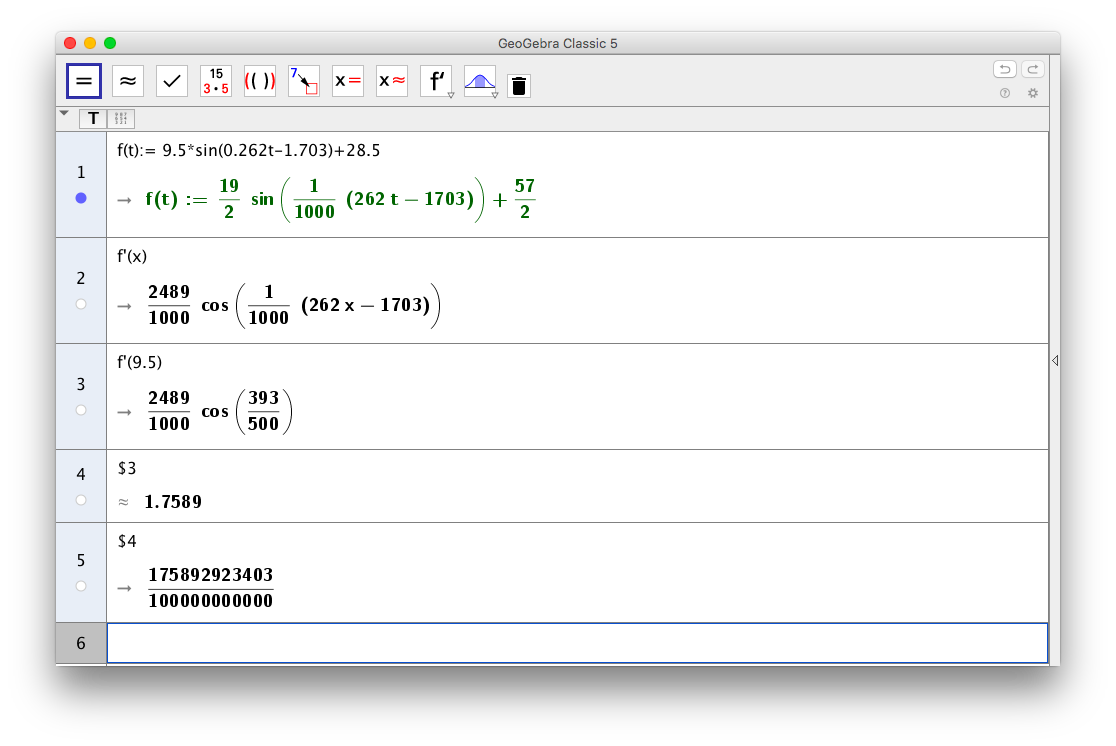
Alltså 1,8o/h.
Märk att rad 2, derivatafunktionen behöver vi inte skriva ut.
- Vilken var temperaturens största förändringshastighet?
Vi undersöker andra derivatans nollställen. Dessa nollställen sätter vi in i derivatafunktionen.
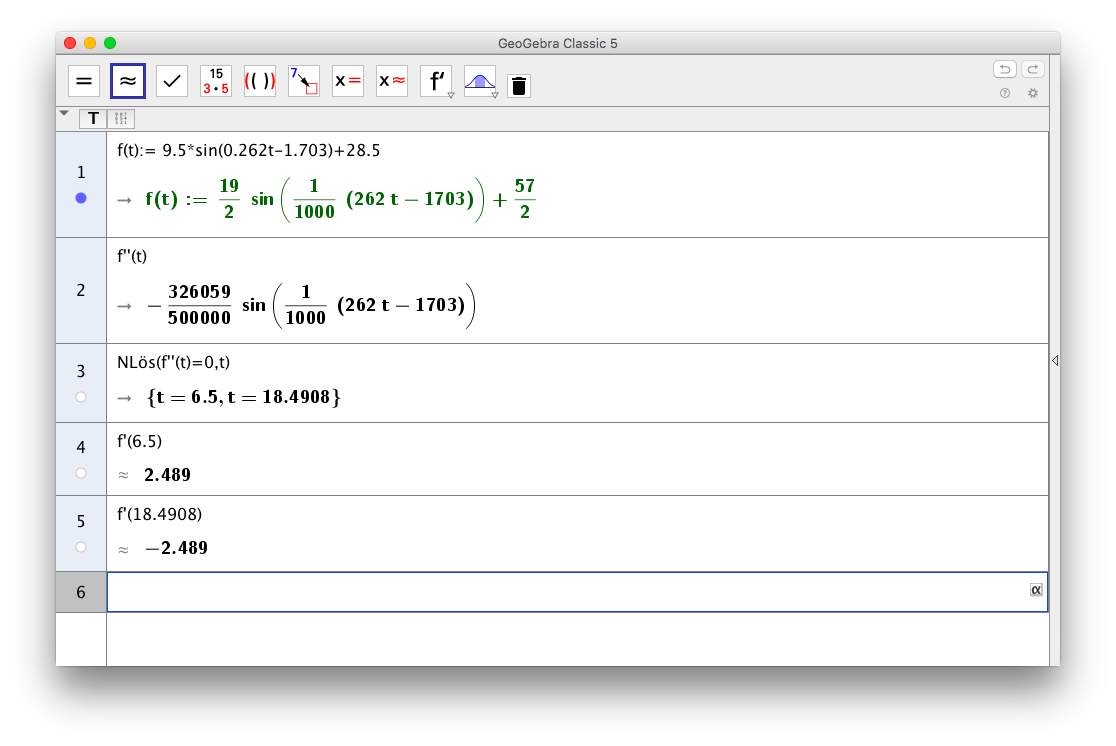
Alltså 2,5o/h.
- Med vilken hastighet förändrades temperaturen kl 9.30?
- Bestäm ekvationen till tangenten för funktionen \( f(x) = 3\tan 2x -2\sin \dfrac{x}{2} \) i den punkt där \( x = 0 \).
\(y\)-koordinaten är \( f(0) = 0\).
Riktningskoefficienten är derivatans värde i \( x=0 \), \( f'(0) = 5 \).
Linjens ekvation är av typ \( y-y_0 = k(x-x_0) \).
Vi får \( y - 0 = 5(x-0) \), alltså \( y = 5x \).
- Bestäm vinkeln mellan grafen till funktionen \( f(x) = 5\cos(7-2x) + 13 \) och \( y \)-axeln med en decimals noggrannhet.
Eftersom \( k = \tan \alpha \), alltså tangensvärdet av vinkeln mellan en linje och \( x \)-axeln är samma som värdet för riktningskoefficienten. Vi vill ha derivatans värde i \( x = 0 \).
\( f'(0) = 10 \sin (7) \).
Vinkeln är 50,6o.
- Vi ritar tangenter till två på varandra följande skärningspunkter mellan kurvan \( f(x) = \sin x \) och \( x \)-axeln. Visa att tangenterna är vinkelräta mot varandra.
Skärningspunkterna är \( sin x =0 \), alltså \( x = n\cdot \pi \). Två punkter för oss är 0 och \( \pi \).
Riktningskoefficienterna är \( f'(0) = 1 \) och \( f'(\pi) = -1 \).
För att två linjer skall vara vinkelräta, ortogonala, gäller att produkten av riktningskoefficienterna har värdet -1, \( k_1\cdot k_2 = -1 \).
Vi har \( 1 \cdot (-1) = -1 \).
Alltså är våra tangenter vinkelräta mot varandra.
- Lös följande ekvationer
- \( \sin x \cos x -\cos^2 x = 0 \)
Vi får:
\( \begin{array}{rcl} \sin x \cos x -\cos^2 x & = & 0 \\ \cos x (\sin x -\cos x) & = & 0 \\ \end{array} \)
Alltså \( \cos x = 0 \). Sker då \( x = \dfrac{\pi}{2} + n\pi \).
Och
\( \begin{array}{rcl} \sin x - \cos x & = & 0 \\ \sin x & = & \cos x \\ \dfrac{\sin x}{\cos x} & = & 1 \\ \tan x & = & 1 \\ \end{array} \)
Vi har förbjudna punkter då \( x = \dfrac{\pi}{2} + n\pi \).
Ekvationen \( \tan x = 1 \) har lösningarna \( x = \dfrac{\pi}{4} +n\pi \).
- \( \sin^2 x -3\cos^2 x = 0 \)
Vi får:
\( \begin{array}{rcl} \sin^2 x -3\cos^2 x & = & 0 \\ \sin^2 x & = & 3\cos^2 x \\ \dfrac{\sin^2 x}{\cos^2 x} & = & 3 \\ \tan^2 x & = & 3 \\ \tan x & = & \pm\sqrt{3} \\ \end{array} \)
\( \tan x = \sqrt{3} \) då \( x = \dfrac{\pi}{3} +n\pi \).
\( \tan x = -\sqrt{3} \) då \( x = \dfrac{2\pi}{3} +n\pi \)
- \( \sin x \cos x -\cos^2 x = 0 \)