8. De trigonometriska funktionerna
När vi behandlar sinus, cosinus och tangens som funktioner har vi vinkeln som funktion av värdemängden.
Genom att ändra på vinkeln, den gröna glidaren, skapar du enhetsciklen (svart) och funktionerna för sinus (grön), cosinus (röd) och tangens (blå). Märk hur funktionerna upprepar sig själv för varje varv på enhetscirkeln.
De trigonometriska funktionerna har följande egenskaper:
| Period | Definitionsmängd | Värdemängd | |
|---|---|---|---|
| Sinus, \( f(x)=\sin x \) | \( 2\pi \) | De reella talen, \( \mathbb{R} \) | [-1,1] |
| Cosinus, \( f(x)=\cos x \) | \( 2\pi \) | De reella talen, \( \mathbb{R} \) | [-1,1] |
| Tangens, \( f(x)=\tan x \) | \( \pi \) | De reella talen förutom \( \dfrac{\pi}{2}+n\pi \) | De reella talen, \( \mathbb{R} \) |
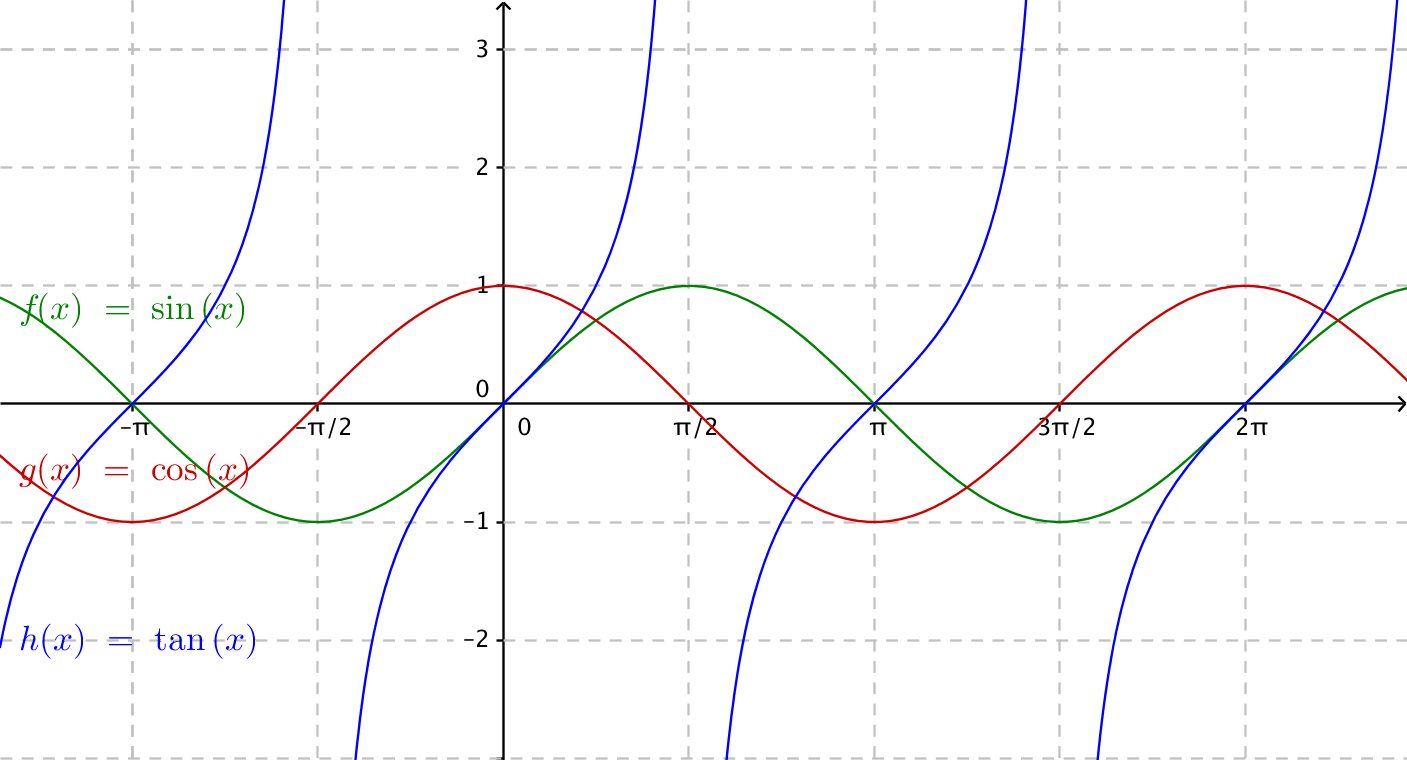
Genom att ändra på vinkeln, tex \( f(x)=\sin 2x \), eller genom att addera till får vi en lite annan funktion. Det får du göra i första uppgiften.
Uppgifter
- Ändra på värdena, A och B, för funktionen \( f(x)=A\sin Bx \) i Geogebra Appen. Hur ändrar A och B på funktionens utseende och egenskaper?
Värdemängden Perioden A ändrar på B ändrar på Värdemängden Perioden A ändrar på B ändrar på - Ändra på värdena, C och D, för funktionen \( f(x)=C+\sin (D+x) \) i Geogebra Appen. Hur ändrar C och D på funktionens utseende och egenskaper?
Ändrar på värdemängden Flyttar på funktionen i sidoled C ändrar på D ändrar på Ändrar på värdemängden Flyttar på funktionen i sidoled C ändrar på D ändrar på - Ändra på värdena, A och B, för funktionen \( f(x)=A\tan Bx \) i Geogebra Appen. Hur ändrar A och B på funktionens utseende och egenskaper?
Flyttar den i sidled. Ändrar på hur snabbt funktionen växer. Ändrar på perioden. A ändrar på B ändrar på Flyttar den i sidled. Ändrar på hur snabbt funktionen växer. Ändrar på perioden. A ändrar på B ändrar på - Ändra på värdena, C och D, för funktionen \( f(x)=C+\tan (D+x) \) i Geogebra Appen. Hur ändrar C och D på funktionens utseende och egenskaper?
Flyttar den uppåt och nedåt. Flyttar den höger och väster. C ändrar på D ändrar på Flyttar den uppåt och nedåt. Flyttar den höger och väster. C ändrar på D ändrar på - Det finns ett samband mellan sinus och cosinus. Ändra på värdena A, B, C och D för \( f(x)=A+B\cos(C+Dx) \) så att funktionen f är identisk med funktionen \( g(x)=\sin x \).Vilket är sambandet mellan sinus och cosinus?
\( \sin x = 1\cos(90^{\circ} - x) \) eller som \( \sin x = \cos(\dfrac{\pi}{2}-x) \).
Eller som \( \sin x = -1\cos(270^{\circ} - x) \) eller som \( \sin x = -\cos(\dfrac{3\pi}{2}-x) \).
- Para ihop rätt funktion med rätt graf. Försök göra det utan att rita upp dem.
Välj bland uttrycken:
\( y=\sin x \)\( y=\tan x \)\( y=1 +\cos x \)\( y=\cos x \)\( y=2\sin x \)\( y=\cos 2x \)Grafen av funktionerna är följande:
Uttryck Grafen av funktionen 





Uttryck Grafen av funktionen \( y=\sin x \) 
\( y=\cos x \) 
\( y=\tan x \) 
\( y=2\sin x \) 
\( y=\cos 2x \) 
\( y=1+\cos x \) 
- Välj för funktionerna rätt värdemängd och period. Det blir två kryss per rad.
Värdemängden [-1,1] Värdemängden [0,2] Värdemängden [-2,2] Perioden \( \pi \) Perioden \( 2\pi \) \( 2\sin x \) \( \sin x \) \( 2\sin 2x \) \( 1+\cos 2x \) \( \sin 2x \) \( 2\cos x \) \( \cos x \) \( 2\cos 2x \) \( 1+\sin x \) \( 1+\sin 2x \) \( \cos 2x \) \( 1+\cos x \) Värdemängden [-1,1] Värdemängden [0,2] Värdemängden [-2,2] Perioden \( \pi \) Perioden \( 2\pi \) \( 2\sin x \) \( \sin x \) \( 2\sin 2x \) \( 1+\cos 2x \) \( \sin 2x \) \( 2\cos x \) \( \cos x \) \( 2\cos 2x \) \( 1+\sin x \) \( 1+\sin 2x \) \( \cos 2x \) \( 1+\cos x \) - Bestäm värdemängden för följande funktioner. Då du vet att \( -1 \leq \sin x \leq 1 \) och att \( -1 \leq \cos x \leq 1 \).
- \( f(x) = 2\sin (x) +3 \)
För sinus gäller att \( -1 \leq \sin (x) \leq 1 \).
Då gäller att \( -2 \leq 2\sin (x) \leq 2 \).
Och att \( -2+3 \leq 2\sin (x) +3 \leq 2+3 \).
Alltså \( 1 \leq 2\sin (x) +3 \leq 5 \).
- \( g(x) = 3\sin 3x -1 \)
För sinus gäller att \( -1 \leq \sin (x) \leq 1 \).
Samma gäller för \( \sin 3x \).
Då gäller att \( -3 \leq 3\sin (3x) \leq 3 \).
Och att \( -3-1 \leq 3\sin (3x) -1 \leq 3-1 \).
Alltså \( -4 \leq 3\sin (3x) -1 \leq 2 \).
- \( h(x) = -2\cos \dfrac{x}{2} +5 \)
För cosinus gäller att \( -1 \leq \cos (x) \leq 1 \).
Samma gäller för \( \cos \dfrac{x}{2} \).
Då gäller att \( -2 \leq 2\cos \dfrac{x}{2} \leq 2 \).
Och för \( -2 \leq -2\cos \dfrac{x}{2} \leq 2 \).
Och att \( -2+5 \leq -2\cos \dfrac{x}{2}+5 \leq 2+5 \).
Alltså \( 3 \leq -2\cos \dfrac{x}{2}+5 \leq 7 \).
- \( f(x) = 2\sin (x) +3 \)
- Utgå från sinusfunktionen och skissa upp följande funktioner utan att använda dig av räknare. Kontrollera svaret genom att rita på GeoGebra.
- \( f(x)= \mid \sin x \mid \)
Eftersom absolutbelopp alltid är positiva får vi något som "speglar" sig i \(x\)-axeln.
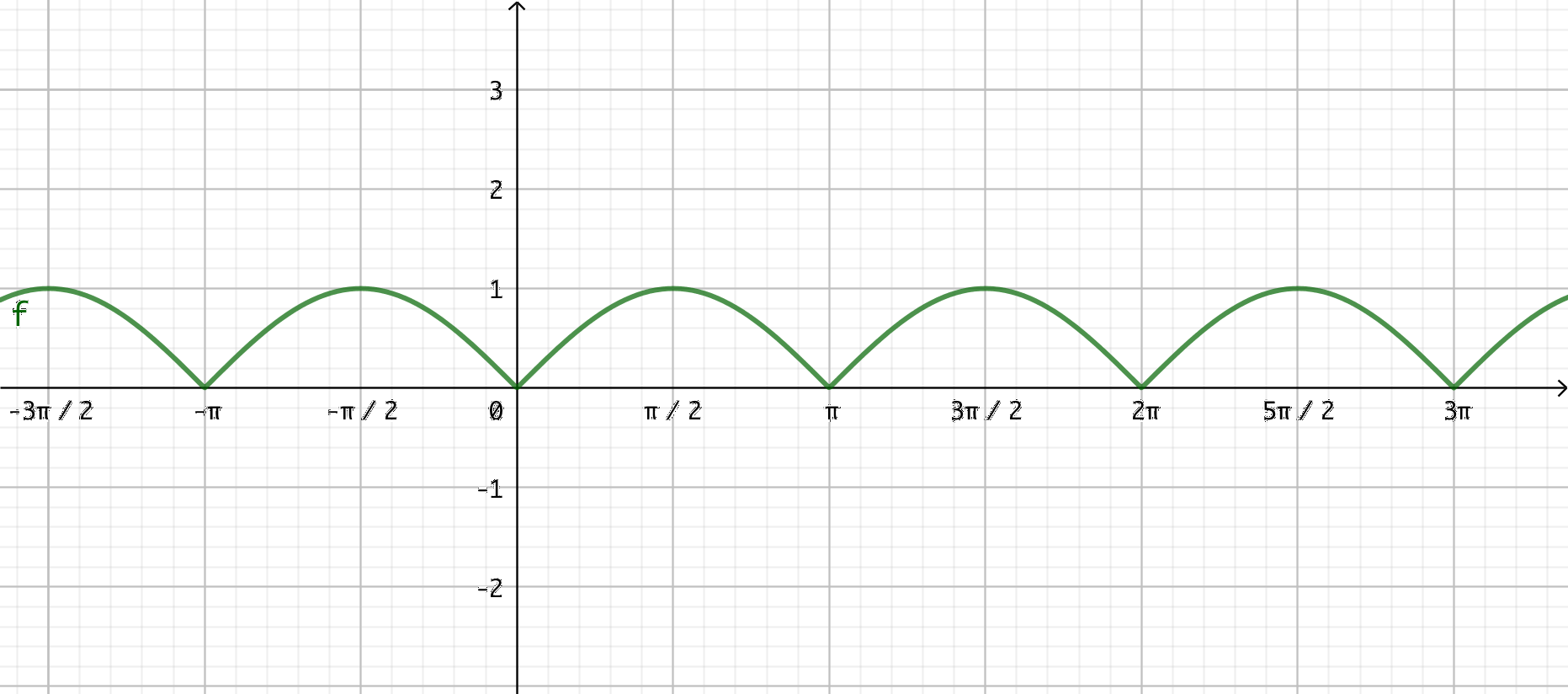
- \( g(x)= \sin x - \mid \sin x \mid \)
Då \( \sin x \) och \( \mid \sin x \) är i olika fas tar de ut varandra. Annars förstärker de varandra.
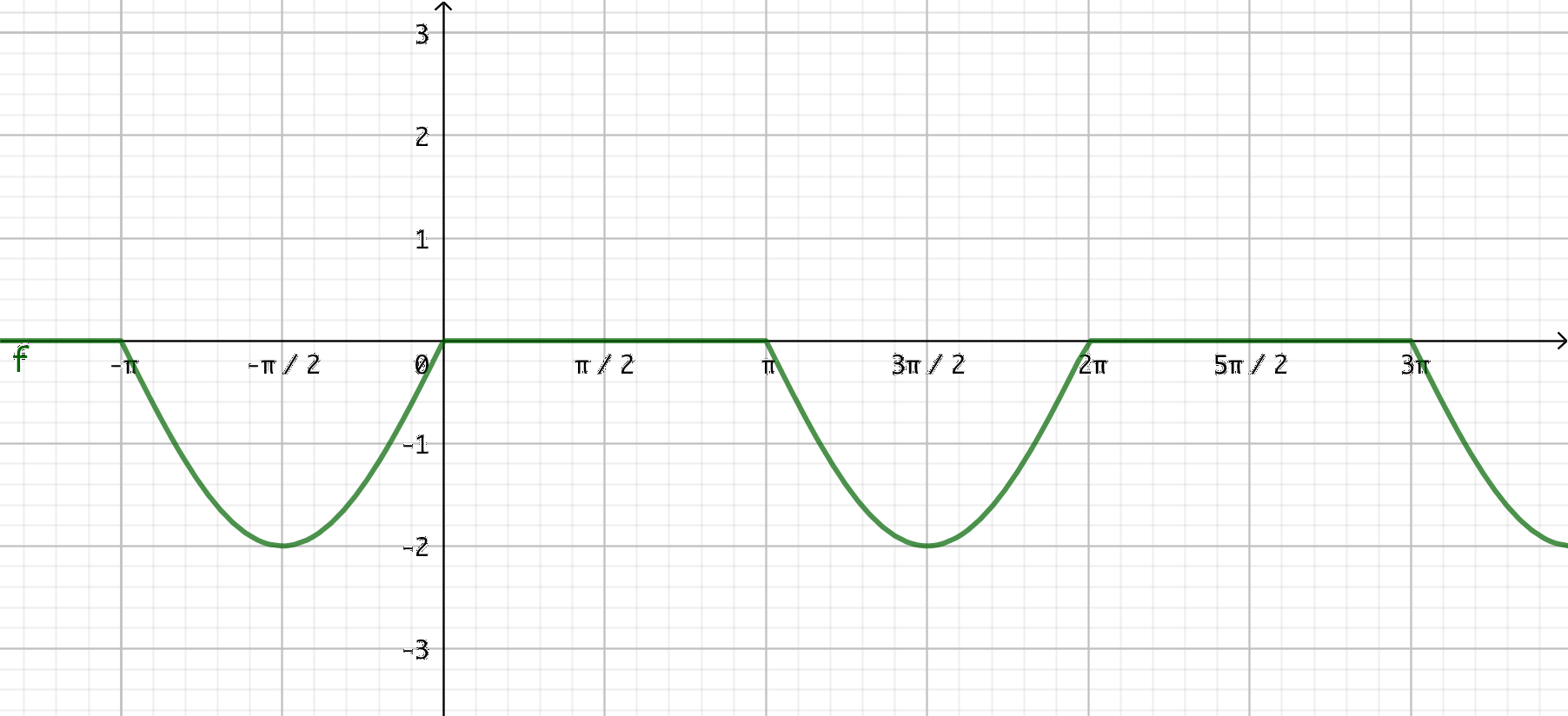
- \( h(x)= \dfrac{\sin x}{\mid \sin x \mid} \)
I punkterna \( n\pi \) får nämnaren värdet 0. Då är \( h \) inte definierad. I intervall där \( \sin x \) är positiv är funktionen ovan \( x \)-axeln, annars är den nedanför \( x \)-axeln. Kvoten har värdet 1 eller -1.
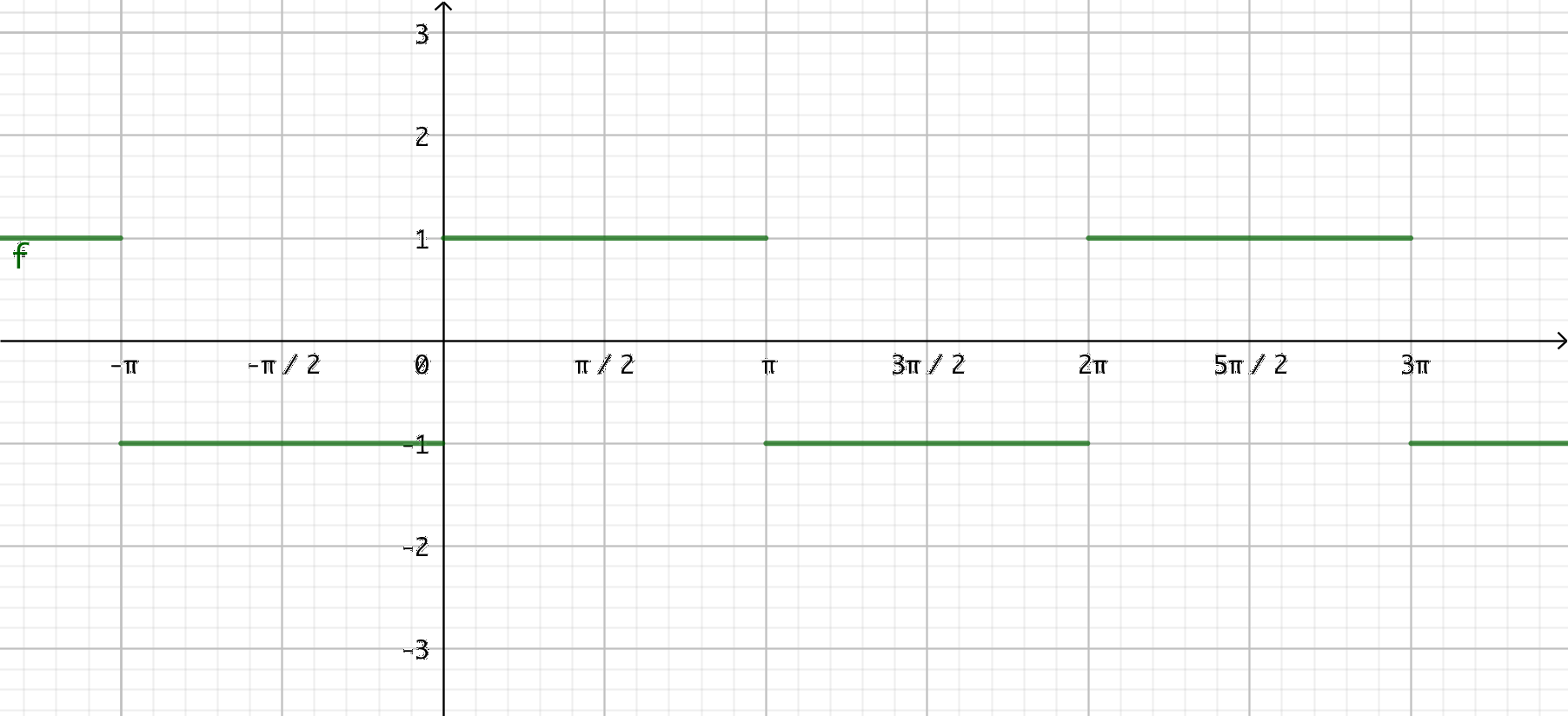
- \( f(x)= \mid \sin x \mid \)