6. Tangens och dess egenskaper

Hittils har vi bekantant oss med sinus och cosinus. Till nästa tar vi och lär oss om tangens. Tangens får vi genom att bilda förhållandet \( \dfrac{\sin x}{\cos x} \).

Exempel 1 Bestäm definitionsmängden för tangens.

Lösning

Eftersom nämnaren inte får få värdet noll så är tangens definierad då \( \cos \alpha \not=0 \). Alltså då \( \alpha \not= \dfrac{\pi}{2}+n\cdot \pi, n \in \mathbb{Z} \).

Då vi kommer ihåg att \( \sin \alpha = \dfrac{\text{motstående katet}}{\text{hypotenusa}} \) och \( \cos \alpha = \dfrac{\text{närliggande katet}}{\text{hypotenusa}} \) får vi att \( \tan \alpha = \dfrac{\sin \alpha}{\cos \alpha} = \dfrac{\dfrac{\text{motstående katet}}{\text{hypotenusa}}}{\dfrac{\text{närliggande katet}}{\text{hypotenusa}}} = \dfrac{\text{motstående katet}}{\text{närliggande katet}} \).

I enhetscirkeln är periferipunktens x-koordinat \( \cos \alpha \) och y-koordinat \( \sin \alpha \). Det betyder att \( \tan \alpha \) är förhållandet mellan periferipunktens koordinater.

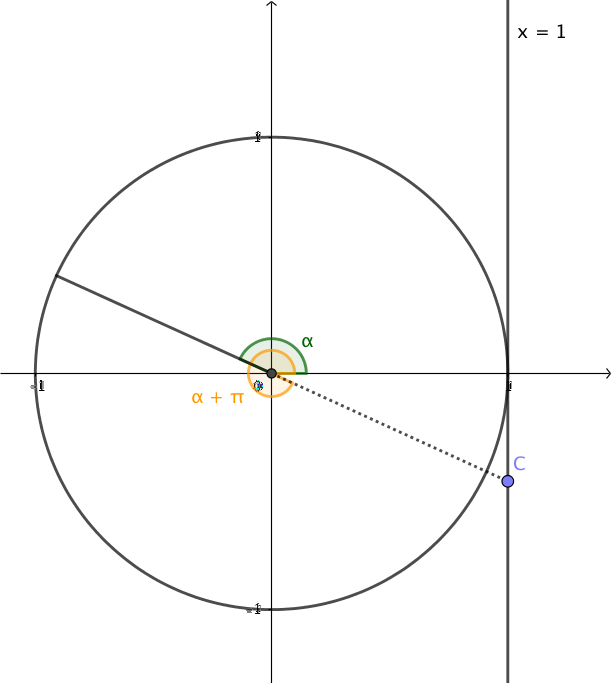
För att bestämma ett värde för \( \tan \alpha \) ser vi förbi periferipunkten och går till skärningspunkten mellan vinlens linje och linjen \( x=1 \), punkt C. Därifrån avläser vi y-koordinaten, punkt D, för att få ett värde för \( \tan \alpha \).

Vi talar om att punkten C är tangentpunkten för vinkeln \( \alpha \). Koordinaterna för tangetpunkten är \( (1, \tan \alpha) \).

Exempel 2 Låt \( \sin \alpha = \dfrac{2}{5} \) och \( \cos \alpha = \dfrac{4}{7} \). Bestäm \( \tan \alpha \).

Lösning

Vi har \( \tan \alpha = \dfrac{\sin\alpha}{\cos\alpha} = \dfrac{\dfrac{2}{5}}{\dfrac{4}{7}} = \dfrac{2}{5}\cdot \dfrac{7}{4} = \dfrac{7}{10} \).

Periodicitet och symmetri hos tangens

Eftersom tangens är y-koordinaten för tangentpunkten märker vi att två vinklar ger samma värde, \( \alpha \) och \( \pi +\alpha \). Vi adderar till ett halvt varv, 180o eller \( \pi \) radianer, och får samma tangetpunkt. Detta kan vi göra med perioden \( \pi \). Perioden hos tangens är alltså \( \pi \).

Alltså gäller \( \tan \alpha = \tan (\alpha + n\cdot \alpha) \) där \( n \in \mathbf{Z} \).

Vidare märker vi att

Vinklarna \( \alpha \) och \( \pi-\alpha \) ger varandras motsatta tal.

Alltså \( \tan \alpha = -\tan(\pi -\alpha) \).

Då vi jämför tangens för vinklarna \( \alpha \) och \( -\alpha \) märker vi att de ger varandras motsatta tal.

Alltså \( \tan \alpha = -\tan(-\alpha) \).

Tangens definieras som, \( \tan x = \dfrac{\sin x}{\cos x} \).

Definitionsmängden för tangens är alla reella tal förutom \( \alpha \not= \dfrac{\pi}{2}+n\cdot \pi, n \in \mathbb{Z} \).

Perioden för tangens är \( \pi \).

För tangens gäller att \( \tan \alpha = \tan (\alpha + n\cdot \alpha) = -\tan(\pi -\alpha) = -\tan(-\alpha) \).

Uppgifter

Bestäm \( \tan\alpha \) i följande fall.
1. Då \( \sin\alpha = \dfrac{2}{3} \) och \( \cos\alpha=\dfrac{5}{6} \).
  
  \( \tan \alpha = \dfrac{\sin\alpha}{\cos\alpha} = \dfrac{\dfrac{2}{3}}{\dfrac{5}{6}} = \dfrac{2}{3} \cdot \dfrac{6}{5} = \dfrac{4}{5} \).
2. Då \( \sin\alpha = \dfrac{1}{2} \) och \( \cos\alpha=\dfrac{3}{4} \).
  
  \( \tan \alpha = \dfrac{\sin\alpha}{\cos\alpha} = \dfrac{\dfrac{1}{2}}{\dfrac{3}{4}} = \dfrac{1}{2} \cdot \dfrac{4}{3} = \dfrac{2}{3} \).
3. Då \( \sin\alpha = \dfrac{1}{3} \) och \( \cos\alpha=\dfrac{3}{5} \).
  
  \( \tan \alpha = \dfrac{\sin\alpha}{\cos\alpha} = \dfrac{\dfrac{1}{3}}{\dfrac{3}{5}} = \dfrac{1}{3} \cdot \dfrac{5}{3} = \dfrac{5}{9} \).
Vi talar om att de trigonometriska funktionerna har teckenschema. Det betyder om de är positiva eller negativa i en viss kvadrant, område i koordinatsystemet. Rita ett koordniatsystem i ditt häfte och bestäm teckenschemat för tangens genom att studera teckenschemat för sinus och cosinus. Skriv plus eller minus i rätt kvadrant.

Vi får \( \begin{array}{c|c}-&+ \\ \hline + & - \\ \end{array} \)
Bestäm på Geogebra appletten tangensvärdet för följande vinklar genom att flytta på punkten A. Vissa vinklar får du inte helt exakt men jobba med det som är närmast. Svara med två decimalers noggrannhet.
1. \( \tan 30^{\circ} \)
2. \( \tan 45^{\circ} \)
3. \( \tan 220^{\circ} \)
4. \( \tan 140^{\circ} \)
1. \( \tan 30^{\circ}=0,58 \)
2. \( \tan 45^{\circ}=1,00 \)
3. \( \tan 220^{\circ}=0,85 \)
4. \( \tan 140^{\circ}=-0,84 \)
Bestäm värdet av tangens genom att du vet periferipunktens koordinater.
1. Vinkeln 0^o har periferipunkten \( (1,0) \). \( \tan0^{\circ} \) har då värdet
  
  \( \tan 0^{\circ} = \dfrac{\sin 0^{\circ}}{\cos 0^{\circ}} = \dfrac{0}{1} = 0 \).
2. Vinkeln \( \dfrac{3\pi}{4} \) har periferipunkten \( (-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}) \). \( \tan \dfrac{3\pi}{4} \) har då värdet
  
  \( \tan \dfrac{3\pi}{4} = \dfrac{\sin \frac{3\pi}{4}}{\cos \frac{3\pi}{4}} = \dfrac{\frac{1}{\sqrt{2}}}{-\frac{1}{\sqrt{2}}} = -1 \)
3. Vinkeln \( \dfrac{\pi}{3} \) har periferipunkten \( (\dfrac{1}{2},\dfrac{\sqrt{3}}{2}) \). \( \tan \dfrac{\pi}{3} \) har då värdet
  
  \( \tan \dfrac{\pi}{3} = \dfrac{\sin \frac{\pi}{3}}{\cos \frac{\pi}{3}} = \dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \dfrac{\sqrt{3}}{2} \cdot \dfrac{2}{1} =\sqrt{3} \).
4. Vinkeln 90^o har periferipunkten \( (0,1) \). \( \tan 90^{\circ} \) har då värdet
  
  \( \tan 90^{\circ} = \dfrac{\sin 90^{\circ}}{\cos 90^{\circ}} = \dfrac{1}{0} \) är ej definierad.
Bestäm exakta värden på \( \cos\alpha \) och \( \tan \alpha \) då \( \sin\alpha=-\dfrac{3}{5} \) och \( \pi < \alpha < \dfrac{3\pi}{2} \).

Eftersom \( \sin\alpha = \dfrac{3}{5} \) så är hypotenusans längd 5 och ena kateten har längden 3. Den andra katetens längd är \( \sqrt{5^2-3^2} = \sqrt{25-9} = \sqrt{16}=4 \).

Eftersom \( \pi < \alpha < \dfrac{3\pi}{2} \) så är \( \cos \alpha < 0 \) och \( \tan \alpha > 0 \).

Vi får att \( \cos \alpha = -\dfrac{4}{5} \) och \( \tan \alpha = \dfrac{3}{4} \).
Bestäm exakta värden på \( \cos\alpha \) och \( \sin \alpha \) då \( \tan\alpha=-3 \) och \( -\dfrac{\pi}{2} < \alpha < 0 \).

Eftersom \( \tan\alpha = -\dfrac{3}{1} \) så är motstånde katets längd 3 och närliggande katets längd 1.

Hypotenusans längd är \( \sqrt{3^2+1^2} = \sqrt{9+1} = \sqrt{10} \).

Eftersom \( -\dfrac{\pi}{2} < \alpha < 0 \) så är \( \sin \alpha < 0 \) och \( \cos \alpha > 0 \).

Vi får att \( \sin \alpha = -\dfrac{3}{\sqrt{10}} \) och \( \cos \alpha = \dfrac{1}{\sqrt{10}} \).
Bestäm sinusvärdet och cosinusvärdet för vinkeln \( \alpha \) då vi vet att \( \tan \alpha = \dfrac{21}{20} \) och
1. \( 0^{\circ} < \alpha < 90^{\circ} \)
  
  Eftersom \( \tan \alpha = \dfrac{21}{20} \) gäller att i en rätvinklig triangel är motstående katet 21 och närliggande katet 20.
  
  Pythagoras sats ger oss längden av hypotenusan, \( \sqrt{20^2+21^2} = 29 \).
  
  Eftersom vinkeln är i första kvadranten är sinus och cosinus positiva.
  
  Vi får \( \cos \alpha = \dfrac{20}{29} \) och \( \sin \alpha =\dfrac{21}{29} \).
2. \( 180^{\circ} < \alpha < 270^{\circ} \)
  
  Eftersom vinkeln är i tredje kvadranten är sinus och cosinus positiva.
  
  Vi får \( \cos \alpha = -\dfrac{20}{29} \) och \( \sin \alpha =-\dfrac{21}{29} \).
3. \( 270^{\circ} < \alpha < 360^{\circ} \)
  
  Eftersom vinkeln är i fjärde kvadranten gäller att tangens är negativ. Men tangens är angiven som positiv och då saknar uppgiften lösning.
Vinkeln \( \alpha \) uppfyller villkoret \( 6\sin\alpha + 4\cos\alpha =0 \). Bestäm exakta värden för \( \sin\alpha \) och \( \cos\alpha \).

\( 6\sin\alpha + 4\cos\alpha =0 \) ger oss att \( \tan \alpha = \dfrac{\sin\alpha}{\cos \alpha}=-\dfrac{4}{6}=-\dfrac{2}{3} \). Kateternas längder är alltså 2 och 3. Hypotenusans längd är \( \sqrt{2^2+3^2}=\sqrt{13} \).

Alltså \( \sin\alpha = \pm\dfrac{2}{\sqrt{13}} \) och \( \cos\alpha = \pm\dfrac{3}{\sqrt{13}} \).

Eftersom \( \tan \alpha \) skall vara negativ måste vi alternera tecknena.

Vinklarna är \( \sin\alpha = \dfrac{2}{\sqrt{13}} \) och \( \cos\alpha = -\dfrac{3}{\sqrt{13}} \) eller \( \sin\alpha = -\dfrac{2}{\sqrt{13}} \) och \( \cos\alpha = \dfrac{3}{\sqrt{13}} \).
Vinkeln \( \alpha \) uppfyller villkoret \( 5\sin\alpha - 2\cos\alpha =0 \). Bestäm exakta värden för \( \sin\alpha \) och \( \cos\alpha \).

\( 5\sin\alpha - 2\cos\alpha =0 \) ger oss att \( \tan \alpha = \dfrac{\sin\alpha}{\cos \alpha}=\dfrac{5}{2}=\dfrac{5}{2} \). Kateternas längder är alltså 5 och 2. Hypotenusans längd är \( \sqrt{5^2+2^2}=\sqrt{29} \).

Alltså \( \sin\alpha = \pm\dfrac{5}{\sqrt{29}} \) och \( \cos\alpha = \pm\dfrac{2}{\sqrt{29}} \).

Eftersom \( \tan \alpha \) skall vara positiv måste vi ha samma tecken.

Vinklarna är \( \sin\alpha = \dfrac{5}{\sqrt{29}} \) och \( \cos\alpha = \dfrac{2}{\sqrt{29}} \) eller \( \sin\alpha = -\dfrac{5}{\sqrt{29}} \) och \( \cos\alpha = -\dfrac{2}{\sqrt{29}} \).
När vi bildade tangens utförde vi divisionen \( \dfrac{\sin x}{\cos x} \). Om vi utför divisionen \( \dfrac{\cos x}{\sin x} \) får vi tangens inversa funktion, cotangens, \( \cot x \). Bestäm definitionsmängden för \( \cot x \).

Eftersom \( \cot x = \dfrac{\cos x}{\sin x} \) är cotangens definierad i alla reella tal förutom då \( \sin x =0 \). Alltså då \( x= 0 +n\cdot \pi \) där \( n \in \mathbf{Z} \).