13. Undersökning av trigonometriska funktioner

Uppgifter

1. Välj för funktionerna rätt värdemängd och period.

   Påstående	Värdemängden \( [-1,1] \)	Värdemängden \( [0,2] \)	Värdemängden \( [-2,2] \)	Perioden \( \pi \)	Perioden \( 2\pi \)
   \( 2\sin x \)
   \( \sin x \)
   \( 2\sin 2x \)
   \( 1+\cos 2x \)
   \( \sin 2x \)
   \( 2\cos x \)
   \( \cos x \)
   \( 2\cos 2x \)
   \( 1+\sin x \)
   \( 1+\sin 2x \)
   \( \cos 2x \)
   \( 1+\cos x \)

   Lösning

   Påstående	Värdemängden \( [-1,1] \)	Värdemängden \( [0,2] \)	Värdemängden \( [-2,2] \)	Perioden \( \pi \)	Perioden \( 2\pi \)
   \( 2\sin x \)
   \( \sin x \)
   \( 2\sin 2x \)
   \( 1+\cos 2x \)
   \( \sin 2x \)
   \( 2\cos x \)
   \( \cos x \)
   \( 2\cos 2x \)
   \( 1+\sin x \)
   \( 1+\sin 2x \)
   \( \cos 2x \)
   \( 1+\cos x \)

2. Kombinera så att följden för algoritmen är sann för hur vi undersöker en trigonometrisk funktion.

   Välj bland följande:

   Beakta periodiciteten eller intervallet som du arbetar med.

   Derivera funktionen.

   Från teckenschemat vet du hur funktionen beter sig och var du hittar största och minsta värden.

   Svara på uppgiften.

   Sök derivatans nollställen, lös alltså ekvationen \( f'(x)=0 \).

   Utgå från derivatans nollställen och bilda ett teckenschema.

   Vad vi skall göra	Ordning
   	1.
   	2.
   	3.
   	4.
   	5.
   	6.

   Lösning

   Vad vi skall göra	Ordning
   Derivera funktionen.	1.
   Sök derivatans nollställen, lös alltså ekvationen \( f'(x)=0 \).	2.
   Utgå från derivatans nollställen och bilda ett teckenschema.	3.
   Från teckenschemat vet du hur funktionen beter sig och var du hittar största och minsta värden.	4.
   Beakta periodiciteten eller intervallet som du arbetar med.	5.
   Svara på uppgiften.	6.

3. Bestäm största och minsta värde för funktionen \( f(x)=2\sin x \). I vilka punkter får funktionen sina största och minsta värden?

   Lösning

   \( f'(x)=2\cos x \). \( f'(x)=0 \) då \( x=\dfrac{\pi}{2}+n \cdot \pi, n \in \mathbb{Z} \). Då vi undersöker funktionen i intervallet \( [0, 2\pi] \) finner vi största och minsta värdena. Våra punkter är \( 0, \dfrac{\pi}{2} \) och \( \dfrac{3\pi}{2} \).

   \( f(0)=f(2 \pi) = 2 \sin 0 = 0 \)

   \( f(\dfrac{\pi}{2}) = 2 \sin (\dfrac{\pi}{2}) = 2\cdot 1 = 2 \)

   \( f(\dfrac{3\pi}{2}) = 2 \sin (\dfrac{3\pi}{2}) = 2\cdot (-1) = -2 \)

   Största värde är \( 2 \), det uppnås i punkterna \( \dfrac{\pi}{2} + n\cdot 2\pi \) och minsta värdet är \( -2 \) som uppnås i punkterna \( \dfrac{3\pi}{2} + n\cdot 2\pi \) där \( n \in \mathbb{Z} \).

4. Bestäm största och minsta värde för funktionen \( f(x)=3\sin 2x \). I vilka punkter får funktionen sina största och minsta värden?

   Lösning

   \( f'(x) = 6\cos 2x \). \( f'(x)=0 \) då \( x=\dfrac{\pi}{4}+n \cdot \dfrac{\pi}{2}, n \in \mathbb{Z} \).

   Funktionen uppreprar sig med intervallet \( \pi \).

   Då vi undersöker funktionen i intervallet \( [0, \pi] \) finner vi största och minsta värdena. Våra punkter är \( \dfrac{\pi}{4} \) och \( \dfrac{3\pi}{4} \).

   \( f(0)=f( \pi) = 3 \sin 2\cdot 0 = 0 \)

   \( f(\dfrac{\pi}{4}) = 3 \sin (2\cdot\dfrac{\pi}{4}) = 3\cdot 1 = 3 \)

   \( f(\dfrac{3\pi}{4}) = 3 \sin (2\cdot\dfrac{3\pi}{4}) = 3\cdot (-1) = -3 \)

   Största värde är \( 3 \), det uppnås i punkterna \( \dfrac{\pi}{4} + n\cdot \pi \) och minsta värdet är \( -3 \) som uppnås i punkterna \( \dfrac{3\pi}{4} + n\cdot \pi \) där \( n \in \mathbb{Z} \).

5. Bestäm största och minsta värde för funktionen \( f(x)=2\cos(x-\pi) \). I vilka punkter får funktionen sina största och minsta värden?

   Lösning

   Eftersom \( \cos(x-\pi) = -\cos x \) kan vi alternativt undersöka den funktionen.

   \( f'(x)=2\sin x \). \( f'(x)=0 \) då \( x=n \cdot \pi, n \in \mathbb{Z} \). Då vi undersöker funktionen i intervallet \( [0, 2\pi] \) finner vi största och minsta värdena. Våra punkter är \( 0, \pi \) och \( 2\pi \).

   \( f(0)=f(2 \pi) = 2 \cos(0-\pi) = 2(-1) = -2 \)

   \( f(\pi) = 2 \cos (\pi-\pi) = 2\cdot \cos 0 = 2\cdot 1 = 2 \).

   Största värde är \( 2 \), det uppnås i punkterna \( \pi + n\cdot 2\pi \) och minsta värdet är \( -2 \) som uppnås i punkterna \( 2\pi + n\cdot 2\pi \) där \( n \in \mathbb{Z} \).

6. Bestäm största och minsta värde för funktionen \( f(x)=-\cos(2x)+1 \). I vilka punkter får funktionen sina största och minsta värden?

   Lösning

   \( f'(x)=2\sin 2x \). \( f'(x)=0 \) då \( x=n \cdot \dfrac{\pi}{2}, n \in \mathbb{Z} \).

   Funktionen uppreprar sig med intervallet \( \pi \).

   Då vi undersöker funktionen i intervallet \( [0, \pi] \) finner vi största och minsta värdena. Våra punkter är \( 0, \dfrac{\pi}{2} \) och \( \pi \).

   \( f(0)=f(\pi) = -\cos(2\cdot 0)+1 = -1 +1 = 0 \)

   \( f(\dfrac{\pi}{2}) = -\cos (2\dfrac{\pi}{2})+1 = 1 + 1 = 2 \).

   Största värde är \( 2 \), det uppnås i punkterna \( \dfrac{\pi}{2} + n\cdot \pi \) och minsta värdet är \( 0 \) som uppnås i punkterna \( \pi + n\cdot \pi \) där \( n \in \mathbb{Z} \).

7. Bestäm största och minsta värde för funktionen \( f(x)=\sin x - \cos x \). I vilka punkter får funktionen sina största och minsta värden?

   Lösning

   Eftersom \( f \) är periodisk räcker det att undersöka den i intervallet \( [0,2\pi] \).

   \( f'(x)=\cos x +\sin x \).

   Nollställena för derivatan är

   \( \begin{array}{rcll} \cos x +\sin x & = & 0 \\ \sin x & = & -\cos x & \mid \cos x \\ \dfrac{\sin x}{\cos x} & = & -1 \\ \tan x & = & -1\\ x & = & \dfrac{3\pi}{4} + n\cdot \pi, n \in \mathbb{Z} \\ \end{array} \)

   Nollställena i intervallet \( [ 0,2\pi ] \) är \( \dfrac{3\pi}{4} \) och \( \dfrac{7\pi}{4} \). Eftersom vi undersöker funktionen i ett intervall sätter vi även i intervallets ändpunkter då vi söker största och minsta värde.

   \( f(0)=f(2\pi)= \sin 0 - \cos 0 = 0 -1 = -1 \).

   \( f(\dfrac{3\pi}{4})=\sin \dfrac{3\pi}{4} - \cos \dfrac{3\pi}{4} = \dfrac{1}{\sqrt{2}} - (-\dfrac{1}{\sqrt{2}}) = \dfrac{1}{\sqrt{2}} + \dfrac{1}{\sqrt{2}} = \dfrac{2}{\sqrt{2}} = \sqrt{2} \).

   \( f(\dfrac{7\pi}{4})=\sin \dfrac{7\pi}{4} - \cos \dfrac{7\pi}{4} = -\dfrac{1}{\sqrt{2}} - \dfrac{1}{\sqrt{2}} = -\dfrac{2}{\sqrt{2}} = -\sqrt{2} \).

   Största värdet är \( \sqrt{2} \) som fås i punkterna \( \dfrac{3\pi}{4} + n\cdot 2\pi \) och minsta värdet är \( -\sqrt{2} \) som fås i punkterna \( \dfrac{7\pi}{4} + n\cdot 2\pi \) där \( n \in \mathbb{Z} \).

8. Låt \( f(x) = 2\tan \dfrac{x}{2} \).
   1. Bestäm definitionsmängden.

      Lösning

      Vi får alla reella tal förutom:

      \( \begin{array}{rcl} \dfrac{x}{2} & \not= & \dfrac{\pi}{2} + n\pi \\ x & \not= & \pi + n2\pi \\ \end{array} \)

   2. Bestäm värdemängden.

      Lösning

      Värdemängden för tangens är alla reella tal. Då är det ingen skillnad om vi multiplicerar med 2. Värdemängden är ändå alla rella tal.

   3. Bestäm tangenten för funktionen i \( x = \dfrac{\pi}{2} \).

      Lösning

      \( f'(x) = 2(1+\tan^2 \dfrac{x}{2})\cdot \dfrac{1}{2} = 1+\tan^2 \dfrac{x}{2} \).

      Riktningskoefficienten, \( f'(\dfrac{\pi}{2}) = 1+1^2 = 2 \).

      \( y \)-koordinaten, \( f(\dfrac{\pi}{2}) = 2 \).

      Tangentens ekvation, \( y - y_0 = k(x-x_0) \). Vi får \( y - 2 = 2(x-\dfrac{\pi}{2}) \), alltså \( y = 2x -\pi +2 \).

9. Bestäm de gemensamma punkterna för \( y=\sin 2x \) och \( y=\sin x \).

   Lösning

   Vi får ekvationen

   \( \begin{array}{rclcrcl} \sin 2x & = & \sin x \\ 2x & = & x +n\cdot 2 \pi & \text{ eller } & 2x & = & \pi-x +n\cdot 2 \pi, n \in \mathbb{Z} \\ x & = & n\cdot 2\pi & & 3x & = & \pi + n\cdot 2\pi \\ & & & & x & = & \dfrac{\pi}{3} + n\cdot \dfrac{2\pi}{3}, n\in \mathbb{Z} \\ \end{array} \)

10. Bestäm de intervall där funktionen \( f(x)=\sin \dfrac{x}{\pi} \) är avtagande.

    Tips

    Perioden för \( f \) är \( [-\pi^2,\pi^2] \), varför?

    Lösning

    \( f'(x)=\dfrac{1}{\pi}\cos\dfrac{x}{\pi} \). Derivatans nollställe är \( x=\dfrac{\pi^2}{2}+n\cdot \pi^2, n \in \mathbb{Z} \).

    Den intressanta punkten är \( -\dfrac{\pi^2}{2} \) och \( \dfrac{\pi^2}{2} \) i intervallet \( [-\pi^2,\pi^2] \).

    Vi gör ett teckenschema:

    \( f'(-2\pi) = \dfrac{1}{\pi}\cos\dfrac{-2\pi}{\pi}= -0,13 < 0 \).

    \( f'(0) = \dfrac{1}{\pi}\cos\dfrac{0\pi}{\pi}= 0,32 > 0 \).

    \( f'(2\pi)= \dfrac{1}{\pi}\cos\dfrac{2\pi}{\pi}= -0,13 < 0 \) .

    \( \begin{array}{r|ccccc} & & -\dfrac{\pi^2}{2} & & \dfrac{\pi^2}{2} \\ \hline f'(x) & - & 0 & + & 0 & - \\ f(x) & \searrow & & \nearrow & & \searrow \\ \end{array} \)

    \( f \) är avtagande i intervallet \( [\dfrac{\pi^2}{2},\dfrac{3\pi^2}{2}] \). Dessa intervall återkommer med perioden \( 2\pi^2 \).

11. Bestäm de gemensamma punkterna för \( f(x)=\sin 2x \) och \( g(x)=3\cos x \).

    Lösning

    Vi löser ekvationen \( f(x)=g(x) \Leftrightarrow \sin 2x = 3\cos x \). \( 3\cos x \) kan vi ersätta med \( 3\sin (\dfrac{\pi}{2}-x) \). Ekvationerna är då \( \sin 2x = 3\sin (\dfrac{\pi}{2}-x) \) som har lösningarna \( \pm \dfrac{\pi}{2}+n\cdot 2\pi, n \in \mathbb{Z} \).

12. Lös ekvationen \( \cos^2 x +\sin x -1 =0 \).

    Lösning

    Då vi utgår från \( \sin^2x + \cos^2 x = 1 \Leftrightarrow \cos^2 x = 1-\sin^2x \).

    Vi får att \( 1-\sin^2 x + \sin x -1 =0 \Leftrightarrow \sin^2 x +\sin x = 0 \Leftrightarrow \sin x(\sin x +1)=0 \).

    Vi tillämpar nollregeln och får att \( \sin x = 0 \) då \( x = n\pi \) och att \( \sin x +1 = 0 \) då \( x=\dfrac{\pi}{2} +n\cdot 2\pi \) där \( n \in \mathbb{Z} \).

13. Lös ekvationen \( \sin^2 x -\cos x =-1 \).

    Lösning

    Då vi utgår från \( \sin^2x + \cos^2 x = 1 \Leftrightarrow \sin^2 x = 1-\cos^2x \).

    Då får vi att \( 1-\cos^2 x -\cos x =-1 \Leftrightarrow -\cos^2 x -\cos x +2 =0 \Leftrightarrow \cos^2 x +\cos x -2 =0 \).

    Vi utför substitueringen \( \cos x = t \) och får \( t^2+t-2=0 \) som har lösningarna \( t=\dfrac{-1\pm3}{2} \), \( t=-2 \) och \( t=1 \).

    Då vi substituterar tillbaka får vi att \( \cos x = -2 \) som saknar lösningar och att \( \cos x = 1 \Leftrightarrow x = n\cdot 2\pi, n\in \mathbb{Z} \).

14. Bestäm tangenterna för funktionen \( f(x)=2\cos x \) som har lutningen 1.

    Lösning

    Eftersom \( \cos x \) har perioden \( 2\pi \) undersöker vi funktionen i intervallet \( [0, 2\pi] \).

    \( f'(x)=2(-\sin x)=-2\sin x \).

    Vi söker \( f'(1)=-2\sin x = -1 \Leftrightarrow \sin x = \dfrac{1}{2} \). Tabell bok ger \( x = \dfrac{\pi}{6} + n\cdot 2\pi, n\in \mathbb{Z} \). I intervallet \( [0,2\pi] \) är lösningen \( \dfrac{\pi}{6} \).

    Tangentens \( y \)-koordinat är \( f(\dfrac{\pi}{6})=2\cos \dfrac{\pi}{6} = 2\cdot \dfrac{\sqrt{3}}{2} = \sqrt{3} \).

    Tangentens ekvation är \( y-y_0 = k(x-x_0) \Leftrightarrow y-\sqrt{3}=1(x-\dfrac{\pi}{6}) \Leftrightarrow y= x -\dfrac{\pi}{6}+\sqrt{3} \). Dessa återkommer då vart \( 2\pi \).

    Alla tangenter är \( y= x -\dfrac{\pi}{6}+\sqrt{3} + n\cdot 2\pi, n\in \mathbb{Z} \).

15. Radien för en halvcirkel är 1. I halvcirkeln är ritat en rektangel så att ena kanten av rektangeln är på halvcirkelns diameter. Vilka dimensioner, längd och bredd, har den rektangel som har den största arean. Arbeta utifrån en vinkel.

    Tips

    

    Lösning

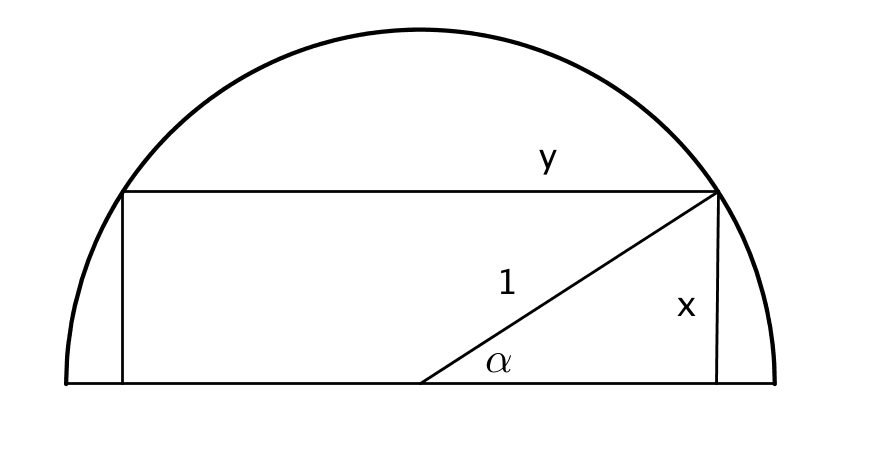
    Längden av höjden är \( x=\sin \alpha \) och halva längden är \( y=\cos \alpha \), \( \alpha \in ]0, \dfrac{\pi}{2}[ \).

    Arean är \( A(\alpha)=\sin \alpha \cdot 2\cos\alpha = 2\sin \alpha \cos \alpha = \sin 2\alpha \).

    \( A'(\alpha)=2\cos2\alpha \). \( A'(\alpha)=0 \) då \( \alpha = \dfrac{\pi}{4}+n\dfrac{\pi}{4}, n\in \mathbb{Z} \).

    I intervallet finns punkten \( \dfrac{\pi}{4} \).

    Höjden är \( \sin \dfrac{\pi}{4} = \dfrac{1}{\sqrt{2}} \) och längden är \( 2\cos \dfrac{\pi}{4} = 2\dfrac{1}{\sqrt{2}}=\sqrt{2} \).

16. Annas morfar som bor i en stuga mitt i skogen. Till stugan kommer man längs en 4,5 km lång rak skogsstig. Från korsningen av skogsstigen och landsvägen finns en transformator på avståndet 12,5 km. Annas morfar vill ha el till stugan och behöver din hjälp så att det är så billigt för honom som möjligt. Det lokala elbolaget erbjuder att dra el genom skogen och längs med landsvägen. Att dra elkabel genom skogen kostar 20 €/m och att dra längs med landsvägen kostar 8 €/m. Vad kostar det som billigast? Lös uppgiften genom att utnyttja en vinkel.

    Lösning

    Då vi kallar sträckan som det skall dras kabel i skogen för \( x \) är sträckan \( x=\dfrac{4500}{\cos \alpha} \) och sträckan längs med landsvägen är \( 12500 -4500\tan \alpha \).

    Funktionen är \( f(\alpha)=20\cdot \dfrac{4500}{\cos \alpha} + 8(12500-4500\tan \alpha) \). För \( \alpha \) gäller \( [0, \dfrac{\pi}{2}[ \) .Härifrån lönar det sig att utnyttja räknare.

    Nollställena är: 0,41 och 2,73 radianer. Av dessa duger endast 0,41 radianer.

    Priset är \( f(0,41)= 182486,48 \text{ €} \approx 182 000 \) euro.

17. Annas farmor bor på en ö som är 1,5 km väst från fastlandet. Rakt norrut längs med fastlandet finns ett postkontor på avståndet 6,0 km. Annas farmor ror med hastigheten 1,0 km/h och går med hastigheten 2,0 km/h. Bestäm den kortaste tid det tar för henne att föra post till postkontoret. Lös uppgiften genom att utnyttja en vinkel.

    Tips

    Tiden kan vi uttrycka som \( t=\dfrac{s}{v} \).

    Lösning

    Sträckan som hon ror, \( x \) är \( x=\dfrac{1,5}{\cos \alpha} \) och sträckan som hon går är \( 6-1,5\tan \alpha \).

    Funktionen som ger tiden är \( t(\alpha)=\dfrac{\dfrac{1,5 \text{ km }}{\cos \alpha}}{1,0 \text{ km/h}} + \dfrac{6-1,5\tan\alpha \text{ km}}{2,0 \text{ km/h}} \) där \( t \in [0,\dfrac{\pi}{2}[ \).

    Derivering och sökandet av derivatans nollställen ger ett minimi då \( \alpha = 0,52 \). \( t(0,52)= 4,3 \) timmar.

18. Fundera på följande tillsammans med en kurskamrat.
    1. Vad är plagiat?
    2. Är "plagierande" samma som att "lunta"?
    3. Om jag apar efter någons underskrift, plagierar jag då hens underskrift?
    4. Om jag delar en idé med någon och hen använder sig av min idé, plagierar hen?
    5. Kan en person ha en idé fastän hen inte berättar den vidare?
    6. Kan en idé existera fastän man inte berättar den vidare?
    7. Tillhör idéer alla eller endast dem som tänker dem?
    8. Om jag plagierar en idé av en annan studerade, men hen märker inte det, kan man ändå tala om plagiat?
    9. Om jag luntar i ett prov och ingen märker det, är det fråga om plagiat?
    10. Är det möjligt att kända vetenskapspersoner har plagierat?
    11. Är en vetenskapsperson som blivit fast för plagiat fortfarande en bra vetenskapsperson?
    12. Kan en vetenskapsperson ha goda orsaker att plagiera?
    13. Är plagiat alltid en allvarlig förseelse?

    Källa: Filosofoidaan matematiikasta ja luonnontieteistä; Daniel, Lafourtune, Pallascio, Sykes