8. Linjens ekvation

Vi studerar den linje som går genom punkten $(1,1)$ och har riktningskoefficienten 2.

Lösning

Nu vet vi inte en annan punkt på linjen så vi tar en allmän med koordinaterna $(x,y)$ . Vi får då

$\begin{array}{l} k=\dfrac{y_2-y_1}{x_2-x_1} \\ 2= \dfrac{y-1}{x-1} \quad \mid (x-1)\\ y-1 = 2(x-1) \\ \end{array}$

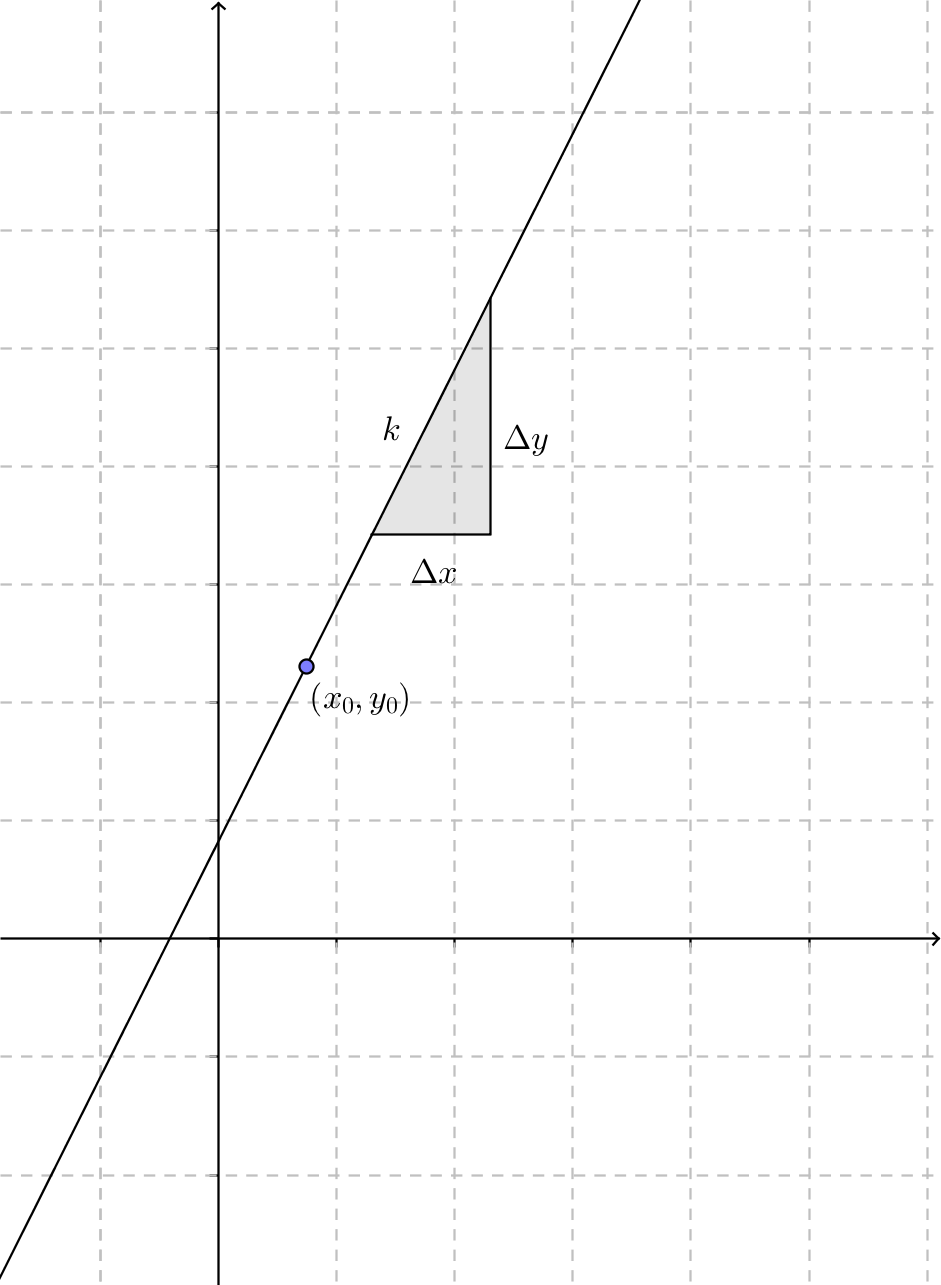
Sitationen ser ut som:

Det som vi får fram är ekvationen för den linje som går genom punkten $(1,1)$ och vars riktningskoefficient är 2.

Allmänt bestämmer vi linjens ekvation som

$y-y_0 = k(x-x_0).$

Exempel 1 Bestäm ekvationen för den linje som går genom punkten $(-2,-1)$ och vars riktningskoefficent är 2.

Lösning

Linjens ekvation får vi som $y-y_0=k(x-x_0)$ .

$\begin{array}{rcl} y-y_0 & = & k(x-x_0) \\ y-(-1) & = & 2(x-(-2)) \\ y+1 & = & 2(x+2) \\ y+1 & = & 2x + 4\\ y & = & 2x +3 \\ \end{array}$

Exempel 2 Bestäm ekvationen för den linje som går genom punkterna $(-1,-1)$ och $(4,3)$ och rita linjen.

Lösning

Linjens ekvation får vi som $y-y_0=k(x-x_0)$ . $k=\dfrac{3-(-1)}{4-(-1)}=\dfrac{4}{5}$ . Då får vi linjen som

$\begin{array}{rcl} y-y_0 & = & k(x-x_0) \\ y-(-1) & = & \dfrac{4}{5}(x-(-1)) \quad \textrm{Vi väljer någondera av punkterna.} \\ y+1 & = & \dfrac{4}{5}(x+1) \\ y & = & \dfrac{4}{5}x + \dfrac{4}{5} -1 \\ y & = & \dfrac{4}{5}x + \dfrac{1}{5} \\ \end{array}$

Grafen ser ut som

Hur vi ritar en linje i ett koordniatsystem

Uppgifter

Bestäm ekvationerna för linjen som går genom punkten $(2,1)$ och har riktningskoefficienten 3.

Vi får $y-y_0=k(x-x_0)$

$y-1=3(x-2)$ som förenklas till $y=3x-5$ .
Bestäm ekvationerna för linjen som går genom punkten $(-3,2)$ och har riktningskoefficienten -4.

Vi får $y-y_0=k(x-x_0)$

$y-2=-4(x-(-3))$ som förenklas till $y=-4x-10$ .
Bestäm ekvationerna för linjen som går genom punkten $(4,-6)$ och har riktningskoefficienten 0.

Vi får $y-y_0=k(x-x_0)$

$y-(-6)=0(x-4)$ som förenklas till $y=-6$ .

Alternativt kan vi märka att vi har en vågrät linje, eftersom riktningskoefficientens värde är 0. Den vågräta linje som går genom punkten $(4,-6)$ är $y = -6$ .
Bestäm ekvationerna för linjerna som går genom punkterna nedan och rita linjerna på papper.
1. $(-4,1)$ och $(0,2)$ .
  
  Riktningskoefficienten är $\dfrac{1-2}{-4-0} = \dfrac{1}{4}$ .
  
  Vi får $y-2 = \dfrac{1}{4}(x-0)$ som förenklas till $y=\dfrac{1}{4}x+2$ .
2. $(-2,3)$ och $(1,1)$ .
  
  Riktningskoefficienten är $\dfrac{3-1}{-2-1} = -\dfrac{2}{3}$ .
  
  Vi får $y-1 = -\dfrac{2}{3}(x-1)$ som förenklas till $y= -\dfrac{2}{3}x+\dfrac{5}{3}$ .
3. $(-2,4)$ och $(3,4)$ .
  
  Riktningskoefficienten är $\dfrac{4-4}{-2-3} = \dfrac{0}{-5} = 0$ .
  
  Vi får $y-4 = 0(x-(-2))$ som förenklas till $y=4$ .
Bestäm ekvationen för linjen som går genom (−2,−2) och (1,4).

Vi har $y-y_0 = \dfrac{\Delta y}{\Delta x}(x-x_0)$ som blir $y-4 = \dfrac{4-(-2)}{1-(-2)}(x-1)$ som förenklas till $y=2x+2$ .
1. Ligger punkten $(0,2)$ på linjen?
  
  Om punkten $(0,2)$ ligger på linjen så skall ekvationen vara sann,
  
  $2 = 2\cdot 0 +2$ som stämmer. Punkten ligger på linjen.
I vilka punkter skär linjen som går genom $(-1,3)$ och $(2,1)$ koordinataxlarna?

Linjens ekvation är $y=-\dfrac{2}{3}x+\dfrac{7}{3}$

Skärningspunkterna för koordinataxlarna får vi då $x=0$ och då $y=0$ . Vi löser dessa ekvationer.

$0=-\dfrac{2}{3}x+\dfrac{7}{3} \Leftrightarrow x=\dfrac{7}{2}$ och
$y=-\dfrac{2}{3}\cdot 0 + \dfrac{7}{3} \Leftrightarrow y=\dfrac{7}{3}$ .
Punkterna är $(0,\dfrac{7}{3})$ och $(\dfrac{7}{2},0)$ .
Linjen $y=kx+7$ går genom punkten $(2,1)$ . Bestäm riktningskoefficienten $k$

Lös uppgiften genom att rita upp situationen på GeoGebra.

Något i stil med

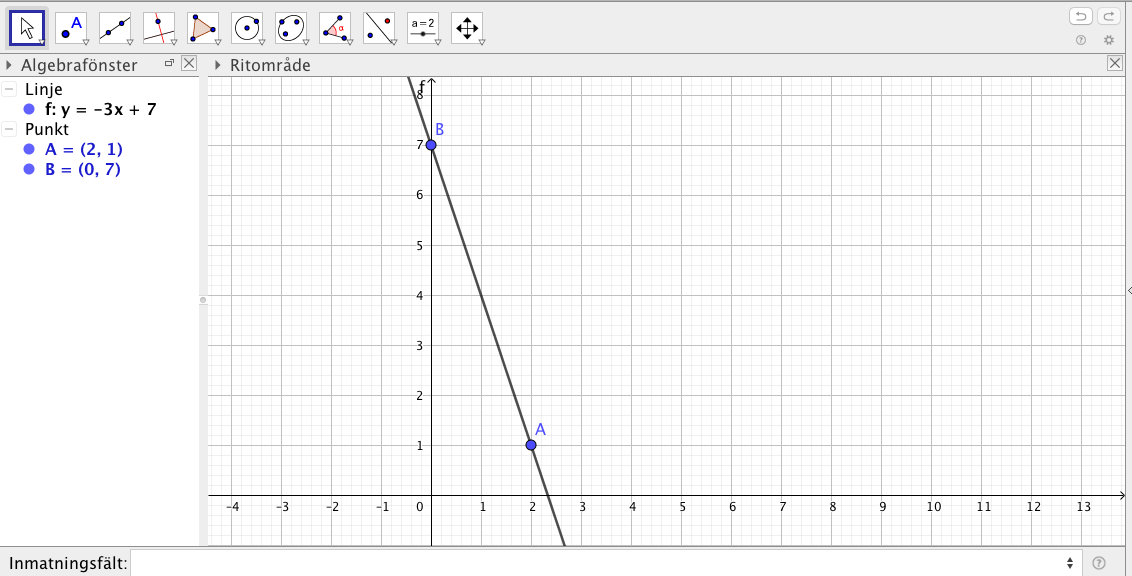
Skapa först punkterna. Sedan en linje mellan punkterna och ändra linjens ekvation så att den är av formen $y=\ldots$ .
Linjen $y=kx+7$ går genom punkten $(2,1)$ . Bestäm riktningskoefficienten $k$ . Lös uppgiften utan att rita på GeoGebra.

Eftersom linjen skall gå genom punkten så skall ekvationen vara sann då $x=2$ och $y=1$ .
Vi löser ekvationen $1=k\cdot 2+7 \Leftrightarrow k=-3$ .
En linje vars riktningskoefficient är $-\dfrac{1}{3}$ avgränsar tillsammans med koordinataxlarna en triangel vars area är 6 a.e. Bestäm ekvationen för linjen.

Skärningspunkten för linjen och $y$ -axeln skriver vi som $(0,y_1)$ och skärningspunkten för linjen och $x$ -axeln som $(x_1,0)$ .

Dessa två punkter skall linjen $y-y_0 = -\dfrac{1}{3}(x-x_0)$ gå igenom.

Vi får ekvationerna $y-y_1 = -\dfrac{1}{3}(x-0)$ och $y-0= -\dfrac{1}{3}(x-x_1)$ .

Dessutom gäller att arean skall ha värdet 6. Arean för en triangel är $A=\dfrac{1}{2}bh$ som är $6=\dfrac{1}{2}\cdot x_1\cdot y_1$ .

Dessa tre ekvationer skall gälla samtidigt och smidigast löser vi dem på räknare. $x_1 = 6$ och $y_1=2$ .

Ekvationen för linjen är $y=-\dfrac{1}{3}x+2$ .