2. Absolutbelopp
Bestäm de tal som har avståndet 2 från nollan på tallinjen. Vilka tal har ett avstånd som är mindre än 1 från nollan på tallinjen?
VIDEO
Absolutbelopp är ett sett att beteckna matematiska avstånd. Avståndet från \( -a \) och \( a \) är lika långt. Vi betecknar avståndet med \( \mid a \mid \).
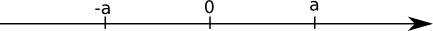
Absolutbelopp definieras som
\( \mid a \mid = \left\{ \begin{array}{rl} a, & \textrm{ då } a \geq 0 \\ -a, & \textrm{ då } a < 0 \\ \end{array}\right. \)
Exempel 1 Bestäm \( \mid -3\mid \) och \( \mid \sqrt{2}-2 \mid \) .
Lösning
\( \mid -3 \mid = 3 \) eftersom avståndet för -3 till 0 är 3.
För att bestämma \( \mid \sqrt{2}-2\mid \) måste vi undersöka storleken av \( \sqrt{2}-2 \). Eftersom \( 1 < \sqrt{2} < 2 \) är \( \sqrt{2} - 2 < 0 \).
Eller så sätter vi det på räknaren, \( \sqrt{2} - 2 \approx -0,58\ldots \).
Per definition är då \( \mid \sqrt{2}-2\mid = -(\sqrt{2}-2) = -\sqrt{2}+2 \).
Egenskaper för absolutbeloppet:
| Egenskap | Exempel |
|---|---|
| \( \mid ab\mid = \mid a \mid \mid b \mid \) | \( \mid 4x \mid = 4\mid x\mid \) och \( \mid -a-b \mid = \mid -(a+b) \mid = \mid -1 \mid \mid a+b \mid = \mid a+b\mid \) |
| \( \mid \dfrac{a}{b} \mid = \dfrac{\mid a \mid }{\mid b \mid}, b\not=0 \) | \( \mid \dfrac{-3}{a} \mid = \dfrac{\mid -3 \mid}{\mid a \mid} = \dfrac{3}{\mid a\mid} \) |
Exempel 2 Skriv \( \mid x^2 -2x+1\mid \) utan absolutbeloppstecken.
Lösning
\( \mid x^2 -2x+1\mid = \mid (x-1)^2 \mid \) som alltid är positivt. Vi får då att \( \mid (x-1)^2 \mid = (x-1)^2 \).
Avståndet mellan två tal \( a \) och \( b \) på tallinjen får vi som \( \mid a-b\mid \).
Exempel 3 Bestäm avståndet mellan
- \( -7 \) och 98
- \( \sqrt{3}-1 \) och \( 2+\sqrt{3} \).
Lösning
- Avståndet mellan -7 och 98 är: \( \mid -7-98\mid = \mid -105\mid = 105 \).
- Avståndet mellan \( \sqrt{3}-1 \) och \( 2+\sqrt{3} \) är:\( \mid (\sqrt{3}-1) - (2+\sqrt{3})\mid = \mid \sqrt{3}-1 -2-\sqrt{3} \mid = \mid -3\mid = 3 \).
Uppgifter
- Bestäm avståndet för talet till noll på tallinjen
- -3
\( \mid -3 \mid =3 \)
- -7
\( \mid -7 \mid =7 \)
- \( 1-\pi \)
\( \mid 1-\pi \mid = -(1-\pi)=\pi-1 \).
- \( -4 + \sqrt{2} \)
\( \mid -4 + \sqrt{2} \mid = -(-4 + \sqrt{2}) = 4 - \sqrt{2} \).
- \( -4 +\sqrt{3} \)
\( \mid -4 +\sqrt{3} \mid = -(-4+\sqrt{3})=4-\sqrt{3} \).
- -3
- Skriv utan absolutbeloppstecken
- \( \mid \sqrt{2}-1\mid \)
Vi har \( 1 < \sqrt{2} < 2 \). Alltså
\( \mid \sqrt{2}-1\mid = \sqrt{2}-1 \)
- \( \mid 1 -\sqrt{3} \mid \)
Vi har \( 1 < \sqrt{3} < 2 \). Alltså
\( \mid 1 -\sqrt{3} \mid =-(1 -\sqrt{3})=\sqrt{3}-1 \)
- \( \mid -2-\sqrt{2}\mid \)
Vi har \( 1 < \sqrt{2} < 2 \). Alltså
\( \mid -2-\sqrt{2}\mid = -(-2-\sqrt{2}) = 2+\sqrt{2} \)
- \( \mid \sqrt{2}-1\mid \)
- Förenkla och bryt ut om det är möjligt.
- \( \mid -4-4x\mid, x>1 \)
\( \mid -4-4x\mid, x>1 \) får vi som \( \mid -4-4x\mid = \mid -4 \mid \cdot \mid 1+x \mid = 4 \mid 1 +x \mid \). Eftersom \( 1 +x > 0 \) då \( x > -1 \) är absolutbeloppet \( \mid 1 + x \mid \) positivt. Alltså \( 4(1+x) \)
- \( \mid 4x^2-4x+1\mid \)
Vi utnyttar det att vi kan skriva det som är innanför absolutbeloppet som en kvadrat och att en kvadrat är alltid positiv.
\( \mid 4x^2-4x+1\mid = \mid(2x-1)^2\mid =(2x-1)^2 \)
- \( \mid \dfrac{x^2-1}{x-1}\mid ,x < -1 \)
Eftersom \( x < -1 \) så gäller att \( \mid \dfrac{x^2-1}{x-1}\mid = \mid \dfrac{(x-1)(x+1)}{x-1} \mid = \mid x+1 \mid = -(x+1)=-x-1 \).
- \( \mid -4-4x\mid, x>1 \)
- Bestäm avståndet mellan
- -3 och 9.
\( \mid -3 -9 \mid = 12 \)
- -12 och -35
\( \mid -12 -(-35) \mid = \mid -12 +35 \mid = \mid 23 \mid = 23 \).
- \( 1-a \) och \( 1+a \).
\( \mid (1-a)-(1+a) \mid = \mid 1-a-1-a \mid = \mid -2a \mid = \mid -2 \mid\cdot \mid a \mid = 2\mid a \mid \).
- \( -\sqrt{2}-1 \) och \( \pi-\sqrt{2} \).
\( \mid (-\sqrt{2}-1)-(\pi -\sqrt{2})\mid = \mid -\sqrt{2}-1-\pi + \sqrt{2}\mid = \mid -1-\pi \mid = -(-1-\pi) = \pi+1 \).
- -3 och 9.
- Bestäm avståndet mellan
- \( 2u \) och \( u-1 \).
\( \mid 2u -(u-1)\mid = \mid u +1 \mid \).
- \( 7-u \) och \( 7+6u \).
Vi får \( \mid (7-u) - (7+6u) \mid = \mid -7u \mid = 7\mid u \mid \).
- \( a-\pi \) och \( b-\pi \).
\( \mid (a-\pi)-(b-\pi) \mid = \mid a-b\mid \).
- \( 3a +1 \) och \( 2-a \), då \( a < \dfrac{1}{4}. \)
\( \mid (3a+1)-(2-a) \mid = \mid 4a -1\mid \). Eftersom \( a<\dfrac{1}{4} \) så får vi att \( \mid 4a-1\mid = -(4a-1)=1-4a \).
- \( 2u \) och \( u-1 \).
- Fundera, utan att titta i nästa kapitel, vilka tal som uppfyller följande ekvationer och olikheter.
- \( \mid x - 30 \mid = 2 \)
\( \mid x - 30 \mid \) handlar om avståndet mellan talet \( x \) och 30. Avståndet skall ha värdet 2.
Från en tallinje märker vi att talen är 28 och 32.
- \( \mid x + 1 \mid = 6 \)
\( \mid x + 1 \mid = \mid x - (-1) \mid \) handlar om avståndet mellan talet \( x \) och -1. Avståndet skall ha värdet 6.
Från en tallinje märker vi att talen är -7 och 5.
- \( \mid x - 20 \mid \leq 5 \)
Vi har avståndet mellan \( x \) och \( 20 \).
Detta avstånd skall vara mindre än 5.
Från en tallinje märker vi att det minsta är 15 och det största är 25.
Alltså \( 15 \leq x \leq 20 \) eller som \( [15,20] \).
- \( \mid x + 50 \mid \leq 3 \)
\( \mid x + 50 \mid \) kan vi skriva som \( \mid x - (-50) \mid \). Vi har avståndet mellan \( x \) och \( -50 \). Detta avstånd skall vara mindre än eller lika med 3.
Från en tallinje märker vi att det minsta är -53 och det största är -47.
Alltså \( -53 \leq x \leq -47 \) eller som \( [-53,-47] \).
- \( \mid x + 3 \mid > 7 \)
\( \mid x + 3 \mid \) kan vi skriva som \( \mid x - (-3) \mid \). Vi har avståndet mellan \( x \) och \( -3 \). Detta avstånd skall vara större än 7.
Från en tallinje märker vi att en gräns är -10 och ennan annan är 4.
Alltså \( x < -10 \) eller \( x > 4 \).
- \( \mid x - 30 \mid = 2 \)
- Visa att avståndet mellan talet \( a +2b \) och \( 6a - 3b \) är fem gånger så långt som mellan talen \( a \) och \( b \).
Avståndet mellan \( a \) och \( b \) är \( \mid a- b \mid \) eller \( \mid b - a \mid \). Ett avstånd som är 5 gånger det är \( 5\mid a- b \mid \) eller \( 5\mid b- a \mid \). Detta skalll vi komma fram till.
Vi får
\( \begin{array}{rcl} \mid (a+2b) - (6a-3b) \mid & = & \mid a+2b -6a+3b \mid \\ & = & \mid -5a +5b \mid \\ & = & 5\mid -a +b \mid \\ & = & 5\mid b -a \mid \\ \end{array} \)
Vi kan också räkna \( \mid -5a +5b \mid = \mid -5 \mid \mid a-b\mid = 5\mid a-b\mid \).
- Ändpunkterna för en sträcka på tallinjen har ändpunkterna \( x_1 \) och \( x_2 \). Visa att mittpunkten för sträckan har värdet av medeltalet av ändpunkterna, \( \dfrac{x_1 + x_2}{2} \).
Vi antar att \( x_1 < x_2 \). Då är avståndet mellan ändpukterna \( x_2 - x_1 \).
Mittpunkten delar sträckan mellan \( x_1 \) och \( x_2 \) i två lika långa delar. Alltså är avståndet från \( x_1 \) till mittpunkten \( \dfrac{1}{2}(x_2 - x_1) \).
Medelpunkten är då
\( \begin{array}{rcl} x_1 + \dfrac{1}{2}(x_2 - x_1) & = & x_1 + \dfrac{1}{2}x_2 - \dfrac{1}{2}x_1 \\ & = & \dfrac{1}{2}x_1 + \dfrac{1}{2}x_2 \\ & = & \dfrac{x_1 + x_2}{2} \\ \end{array} \)
- Undersök för hurdana värden på \( a\not=0 \) och \( b\not=0 \) gäller följande?
- \( \mid a+b \mid = \mid a \mid + \mid b\mid \)
Då a och b har samma tecken, båda positiva eller negativa.
- \( \mid a-b \mid = \mid a \mid - \mid b\mid \)
Då a och b har samma tecken och \( \mid a\mid \geq \mid b\mid \).
- \( \mid a+b \mid = \mid a \mid - \mid b\mid \)
Då a och b har olika tecken och \( \mid a \mid \geq \mid b\mid \).
- \( \mid a-b \mid = \mid\mid a \mid - \mid b\mid\mid \)
Då a och b har samma tecken.
- \( \mid a+b \mid = \mid a \mid + \mid b\mid \)