6. Punktmängder

Vi prickar in de punkter i ett koordinatsystem som uppfyller sambandet $x+y=5$ .

Exempel 1 Visa att punkterna $(0,5)$ , $(-3,4)$ och $(-4,3)$ uppfyller ekvationen $x^2+y^2=25$ . Vilka andra punkter uppfyller ekvationen? Vad bildar punktmängden?

Exempel 2 Ekvationen för en punktmängd är $x^2-4x-y=0$ . Är punkterna $(2,0)$ , $(0,0)$ och $(2,-4)$ punkter i punktmängden? Vad bildar punktmängden?

De talpar som uppfyller en ekvation bildar punkter av grafen. Vi får reda på om punkterna är i punktmängden genom att sätta in punkterna i punktmängden.

Uppgifter

Låt punktmängden vara $xy^2-y=0$ . Är punkterna $(-1,-1)$ , $(1,1)$ och $(2,1)$ punkter i punktmängden?

$(-1,-1)$ och $(1,1)$ är punkter för punktmängden. $(2,1)$ är inte eftersom ekvationen inte satifieras.
Rita punktmängden $xy^2-y=0$ på papper. Du kommer att behöva flera punkter en de två som du fick i uppgiften ovan.

$xy^2-y=0$ kan vi skriva som $y(xy - 1)=0$ .

Punktmängden består av $y = 0$ och $xy-1 =0$ som är $y = \dfrac{1}{x}$ .

Punktmängden ser ut som
Rita punktmängden $x^2-xy = 0$ . Börja med att studera vad den består av. Rita sedan på papper och kontrollera din lösning på GeoGebra eller motsvarande.

$x^2-xy = 0$ kan vi skriva som $x(x-y)=0$ .

Punktmängden består av linjerna $x = 0$ och $x-y=0$ som är samma som $y = x$ .

Vi får
Ekvationen för en punktmängd är x2+y=0.
1. Undersök om punkterna $A = (-1,1)$ , $B = (-2,4)$ , $C = (-3,-9)$ och $D = (\sqrt{5},-5)$ är punkter i punktmängden.
  
  A: $(-1)^2 + 1 = 2$ . Inte punkt i punktmängden.
  
  B: $(-2)^2 + 4 = 8$ . Inte punkt i punktmängden.
  
  C: $(-3)^2 -9 = 0$ . Punkt i punktmängden.
  
  D: $(\sqrt{5})^2 +(-5) = 10$ . Punkt i punktmängden.
2. Studera vad punktmängden består av. Bestäm eventuellt några punkter och skissa upp punktmängden på papper. Granska sedan din lösning på GeoGebra eller motsvarande.
  
  $x^2 + y = 0$ är samma som $y = -x^2$ .
  
  Vi har en parabel som öppnar sig nedåt.
Rita följande punktmängder på papper. Granska din lösning genom att rita punktmängden på GeoGebra eller motsvarande.
1. $x-1=0$
2. $y+3=0$
3. $(x-1)(y+3)=0$
Något i stil med
Rita följande punktmängder på papper. Granska din lösning genom att rita punktmängden på GeoGebra eller motsvarande.
1. $x-2=0$
2. $y-4=0$
3. $(x-2)(y-4)=0$
Något i stil med
Rita punktmängderna vars ekvationer är $x^2-y^2=0$ och $x^2+y^2=0$ .

$x^2 - y^2 = 0$ är samma som $y^2 = x^2$ .

$x^2+y^2=0$ är en punkt i origo.

Något i stil med
Rita punktmängden $\mid x-y \mid = 2$

$\mid x-y \mid = 2$ består av $x -y = 2$ som är $y = x-2$ och $x -y = -2$ som är $y = x+2$ .

Punktmängden är
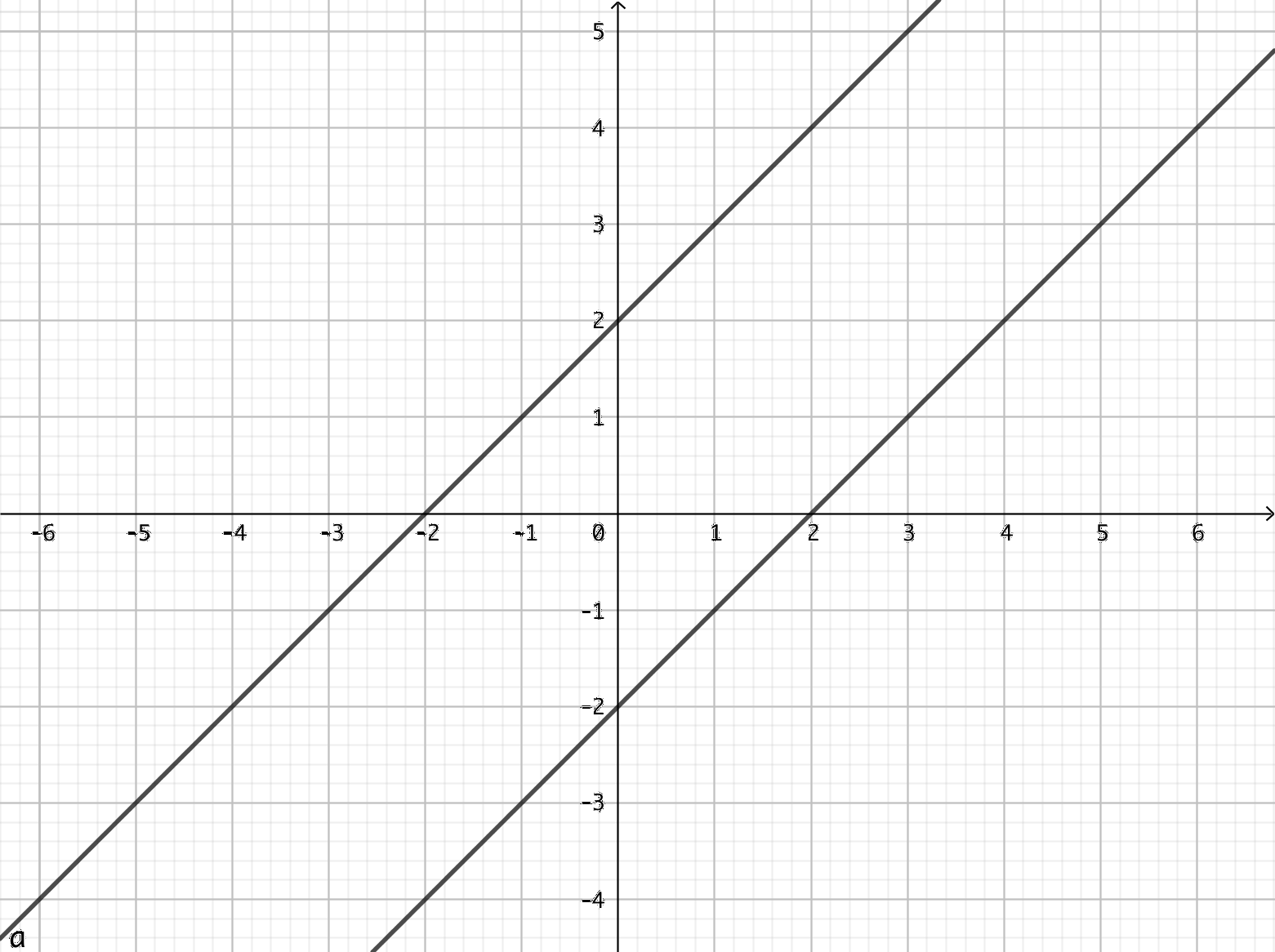
Rita punktmängden $\mid x-2 \mid = \mid y \mid$ .

$\mid x-2 \mid = \mid y \mid$ består av $x -2 = y$ som är $y = x-2$ och $x -2 = -y$ som är $y = -x+2$ .

Punktmängden är
Rita punktmängden $\mid x-y\mid = \mid y\mid$ .

Vi har $x-y = y$ som är $y = \dfrac{1}{x}$ och $x-y = -y$ som är $x=0$ .

Något i stil med
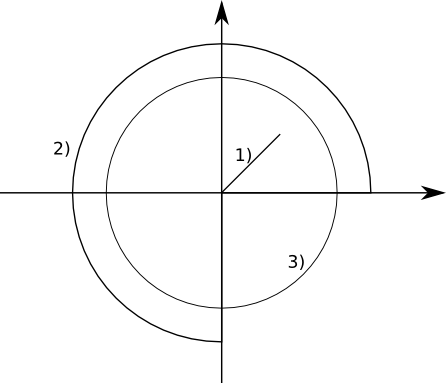
Rita följande polära punktmängder.
1. $r \leq 2$ , och $\theta = 45^{\circ}$
2. $r = 4$ , och $0 \leq \theta \leq 270^{\circ}$
3. $r=3$
Något i stil med