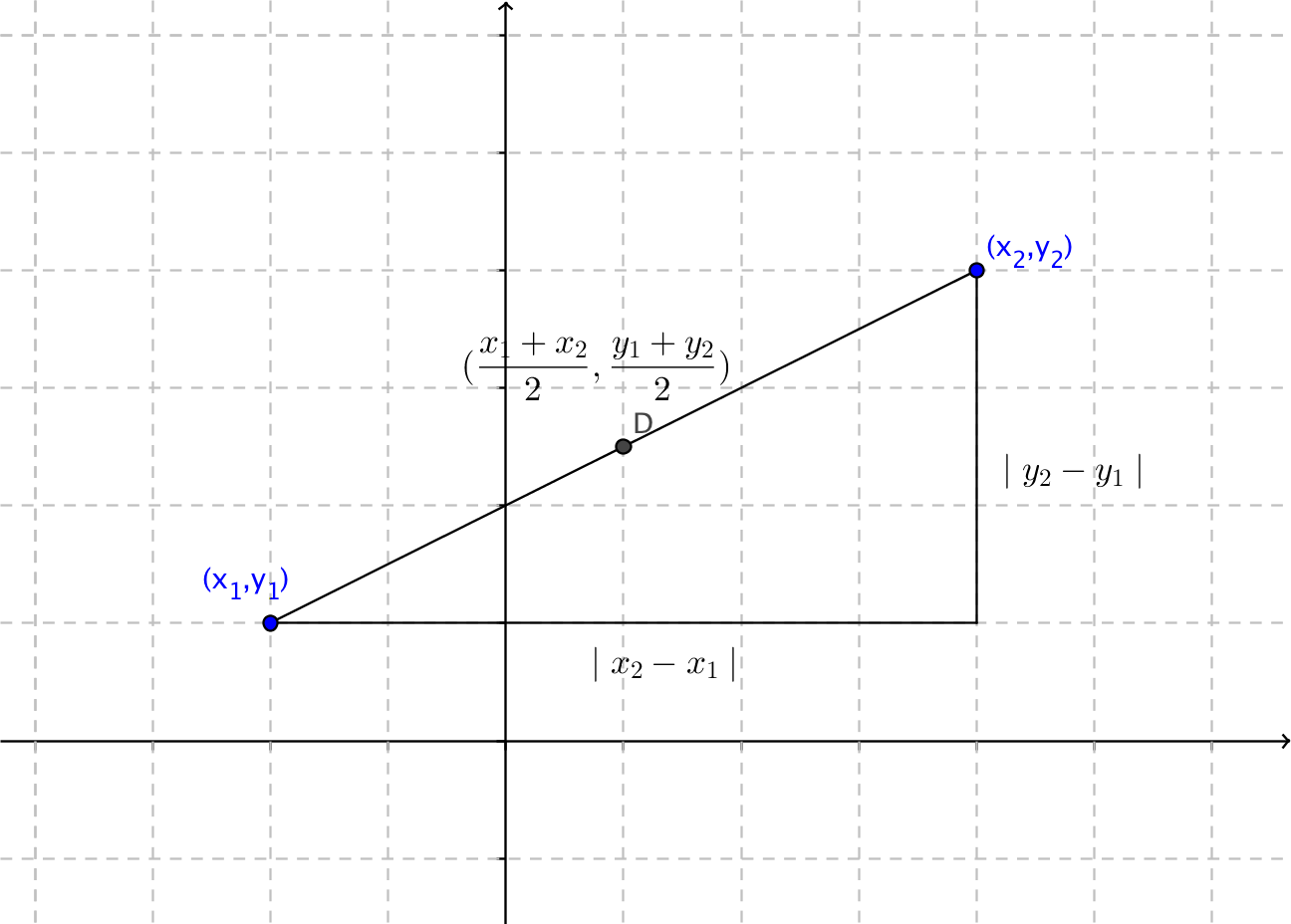
5. Mittpunkt av en sträcka

Mittpunkten för en sträcka mellan \( (x_1,y_1) \) och \( (x_2,y_2) \) får vi via \( (\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}) \).

Exempel 1 Bestäm punkten som befinner sig mitt emellan \( (-3,-2) \) och \( (4,0) \).

Lösning

Vi får x-koordinaten får vi som \( \dfrac{-3+4}{2}= \dfrac{1}{2} \) och y-koordinaten som \( \dfrac{-2+0}{2}=-1 \). Mittpunkten är \( (\dfrac{1}{2},-1) \) .

Exempel 2 Bestäm ändpunkten då vi vet att sträckan från \( (-4,-5) \) har en mittpunkt i \( (0,-3) \).

Lösning

Vi får ändpunktens x-koordinat via \( 0=\dfrac{-4+x}{2} \) som ger \( x=4 \) och \( y \)-koordinaten via \( -3=\dfrac{-5+y}{2} \) som \( y=-1 \). Ändpunkten är \( (4,-1) \) .

Uppgifter

Bestäm mittpunkten för sträckan mellan
1. \( (-1,-3) \) och \( (1,1) \).
  
  Vi får \( (\dfrac{-1+1}{2}, \dfrac{-3+1}{2}) = (0,-1) \).
2. \( (3,2) \) och \( (-1,2) \).
  
  Vi får \( (\dfrac{3-1}{2}, \dfrac{2+2}{2}) = (1,2).
3. \( (3,1) \) och \( (-1,-3) \).
  
  Vi får \( (\dfrac{3+(-1)}{2}, \dfrac{1+(-3)}{2}) = (1,-1) \).
Bestäm mittpunkten för sträckan mellan
1. \( (-\sqrt{2},-1) \) och \( (7\sqrt{2},3) \).
  
  Vi får \( \dfrac{-\sqrt{2}+7\sqrt{2}}{2} = \dfrac{6\sqrt{2}}{2} = 3\sqrt{2} \),
  
  och \( \dfrac{-1+3}{2} = 1 \).
  
  Alltså \( (3\sqrt{2},1) \).
2. \( (2\sqrt{3},-6) \) och \( (4\sqrt{3},-4) \).
  
  Vi får \( \dfrac{2\sqrt{3}+4\sqrt{3}}{2} = \dfrac{6\sqrt{3}}{2} = 3\sqrt{3} \),
  
  och \( \dfrac{-6-4}{2} = -5 \).
  
  Alltså \( (3\sqrt{3},-5) \).
3. \( (3\sqrt{2},-2) \) och \( (-2\sqrt{2},8) \).
  
  Vi får \( \dfrac{3\sqrt{2}-2\sqrt{2}}{2} = \dfrac{\sqrt{2}}{2} = \dfrac{\sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \dfrac{1}{\sqrt{2}} \),
  
  och \( \dfrac{-2+8}{2} = 3 \).
  
  Alltså \( (\dfrac{1}{\sqrt{2}},3) \).
Bestäm ändpunkten och längden av sträckan som börjar i \( (-3,-2) \) och vars mittpunkt är i \( (-2,2) \).

Ändpunkten: \( (\dfrac{-3+x}{2}, \dfrac{-2+y}{2}) = (-2,2) \) som ger koordinaterna (-1,6).

Längden \( \sqrt{(-3-(-1))^2+(-2-6)^2} = \sqrt{68}=2\sqrt{17} \).
Bestäm ändpunkten och längden av sträckan som börjar i origo och vars mittpunkt är \( (a,b) \).

Ändpunkten: \( (\dfrac{0+x}{2}, \dfrac{0+y}{2}) = (a,b) \) som ger koordinaterna \( (2a,2b) \).

Längden \( \sqrt{(2a-0)^2+(2b-0)^2} = \sqrt{4a^2+4b^2} = 2\sqrt{a^2+b^2} \).
Bestäm arean av den kvadrat som uppstår då man halverar sidorna i kvadraten vars hörnpunkter är \( (-2,0) \), \( (1,1) \), \( (2,-2) \) och \( (-1,-3) \).

Bestäm mittpunten mellan två hörnpunkter, tex E =\( (\dfrac{-2+1}{2}, \dfrac{0+1}{2}) = (-\dfrac{1}{2},\dfrac{1}{2}) \) och H = \( (\dfrac{1+2}{2}, \dfrac{1+(-2)}{2}) = (\dfrac{3}{2},-\dfrac{1}{2}) \).

Avståndet EH är \( \sqrt{(-\dfrac{1}{2}-\dfrac{3}{2})^2+(\dfrac{1}{2}-(-\dfrac{1}{2}))^2} = \sqrt{5} \).

Arean är \( (\sqrt{5})^2=5 \).