10. Cirkeln
Bestäm den punktmängd som är på avståndet 2 från punkten \( (1,1) \).
Lösning
Vi utnyttjar avståndet mellan två punkter, \( d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \). De punkter som vi arbetar med är \( (1,1) \) och \( (x,y) \) och avståndet mellan dessa skall vara 2.
Vi får att
\( \begin{array}{rcll} d & = & \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ 2 & = & \sqrt{(x-1)^2+(y-1)^2} & \mid (\quad)^2 \\ 2^2 & = & (x-1)^2 + (y-1)^2 \\ \end{array} \)
Den punktmängd som beskriver de punkter som har med avståndet 2 till (1,1) är de (x,y) som uppfyller ekvationen \( 2^2 = (x-1)^2 + (y-1)^2 \).
Ritar vi det i ett koordinatsystem så har vi en cirkel.

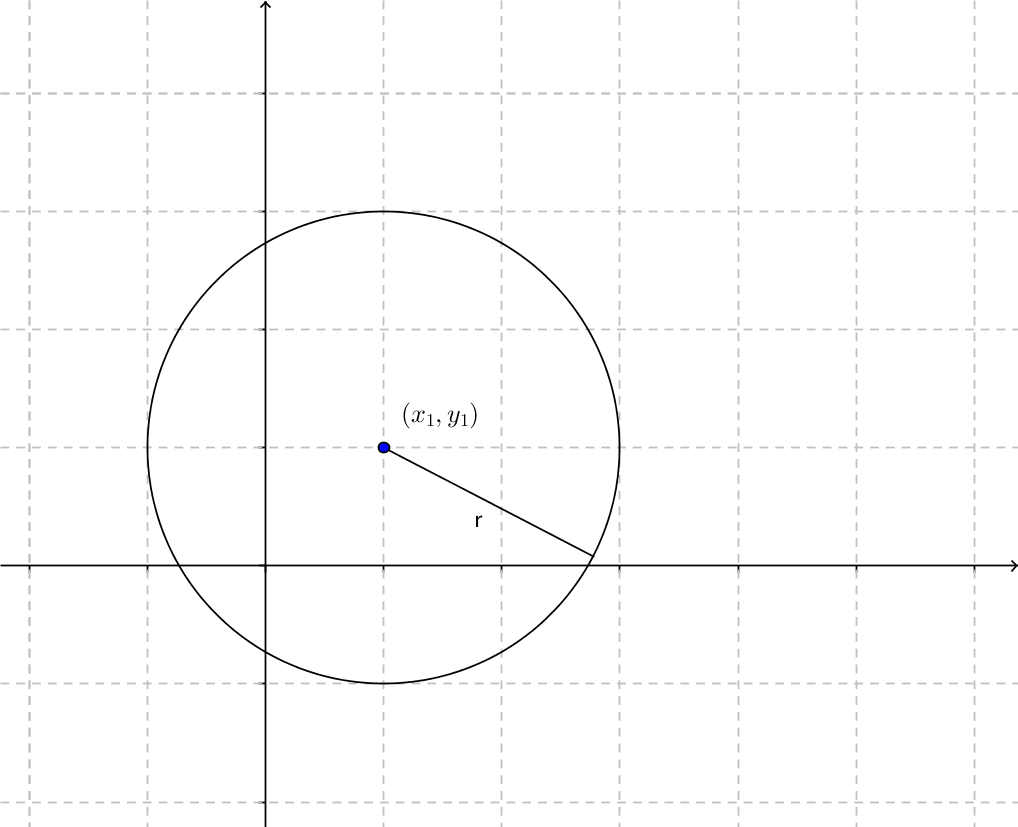
Cirkelns ekvation lyder som \( (x-x_1)^2 + (y-y_1)^2 = r^2 \). Punkten \( (x_1, y_1) \) är cirkelns mittpunkt och \( r \) är cirkelns radie.
Exempel 1 En cirkel har mittpunkten \( (0,2) \) och radien 4.
- Bestäm ekvationen för cirkeln.
- Är punkten \( (4,3) \) på cirkeln?
Lösning
- Ekvationen för cirkeln får vi som:
\( \begin{array}{rcl} (0-x)^2 + (y-2)^2 & = & 4^2 \\ x^2 + (y-2)^2 & = & 16 \\ \end{array} \)
- Om punkten \( (4,3) \) skall vara på cirkeln skall uttrycket vara sant, \( 4^2 + (3-2)^2 = 16+1 \not= 16 \) som det borde vara. Punkten \( (4,3) \) ligger inte på cirkeln.
Vi ritar cirklar på GeoGebra
Uppgifter
- Bestäm mittpunkt och radie för
- \( (x-3)^2+(y-5)^2 = 4 \)
Mittpunkten är \( (3,5) \) och radien är \( \sqrt{4}=2 \).
- \( (x+1)^2+(y-2)^2 = 1 \)
Mittpunkten är \( (-1,2) \) och radien är \( \sqrt{1}=1 \).
- \( (x+3)^2+y^2 = 5 \)
Mittpunkten är \( (-3,0) \) och radien är \( \sqrt{5} \).
- \( (x-3)^2+(y-5)^2 = 4 \)
- Ligger punkterna \( (1,-1) \), \( (-1,-2) \) och \( (3,-3) \) på cirkeln \( (x-1)^2+(y+3)^2=4 \)?
Insättning av punkternas koordinater i ekvationen ger att \( (1,-1) \) och \( (3,-3) \) ligger på cirkeln. \( (-1,-2) \) ligger inte.
- Bestäm ekvationen för följande cirklar.
- Mittpunkt är \( (1,1) \) och radien är 3.
\( (x-1)^2+(y-1)^2 = 9 \)
- Mittpunkt är \( (0,0) \) och radien är 2.
\( x^2+y^2=4 \)
- Mittpunkt är \( (-1,-2) \) och radien är \( \sqrt{2} \).
\( (x+1)^2+(y+2)^2=2 \)
- Mittpunkt är \( (1,1) \) och radien är 3.
- Tre hörnpunkter för en kvadrat är \( (-4,2) \), \( (2,2) \) och \( (2,8) \).
- Bestäm ekvationen för den cirkel som är inskriven kvadraten.
Den fjärde hörnpunkten är \( (-4,8) \).
Mittpunkten i kvadraten är \( (-1,5) \). Se till att du löser den!
Eftersom cirkeln skall rymmas i kvadraten är radien halva sidan.
Cirkelns ekvation är \( (x+1)^2 + (y-5)^2 = 9 \).
- Bestäm ekvationen för den cirkel som är omskriven kvadraten.
Mittpunkten är samma som ovan.
Eftersom cirkeln skall vara runt kvadraten är radien halva diagonalen.
Cirkelns ekvation är \( (x+1)^2 + (y-5)^2 = 18 \).
- Bestäm ekvationen för den cirkel som är inskriven kvadraten.
- Rita cirklarna \( (x+2)^2+(y+1)^2=4 \) och \( (x-1)^2+(y-3)^2=1 \) och bestäm avståndet mellan dem. Med avstånd mellan två punktmängder gäller det kortaste avstånd mellan två punkter på punktmängderna.
Cirklarna har mittpunkterna \( (-2,-1) \) och \( (1,3) \). Avståndet mellan mittpunkterna är \( \sqrt{(-2-1)^2+(-1-3)^2}=5 \).
Eftersom cirklarna har radierna 2 och 1 så blir avståndet mellan cirklarna \( 5-2-1=2 \) l.e.
- Bestäm avståndet mellan cirklarna \( (x+2)^2+(y+2)^2=2 \) och \( (x-1)^2+(y-1)^2=2 \).
Cirklarna har mittpunkterna \( (-2,-2) \) och \( (1,1) \). Avståndet mellan mittpunkterna är \( \sqrt{(-2-1)^2+(-2-1)^2}=\sqrt{18}=3\sqrt{2} \).
Bägge cirklarna har radien \( \sqrt{2} \). Avståndet mellan cirklarna är \( 3\sqrt{2}-2\sqrt{2}=\sqrt{2} \).
- Bestäm avståndet mellan cirklarna \( (x+6)^2+(y-5)^2=9 \) och \( (x-2)^2+(y+2)^2=1 \).
Cirklarna har mittpunkterna \( (-6,5) \) och \( (2,-2) \). Avståndet mellan mittpunkterna är \( \sqrt{113} \).
Cirklarna har radierna 3 och 1.
Avståndet mellan cirklarna är \( \sqrt{113}-3-1=\sqrt{113}-4 \).
- Bestäm avståndet mellan cirklarna \( (x+3)^2+(y-2)^2=16 \) och \( (x+2)^2+(y-1)^2=1 \).
Cirklarna har mittpunkterna \( (-3,2) \) och \( (-2,1) \). Avståndet mellan mittpunkterna är \( \sqrt{2} \).
Ena cirkeln har radien 4 och den andra 1. Märk att den ena cirkeln är inne i den andra.
Avståndet mellan cirklarna är \( 4-1-\sqrt{2}= 3 - \sqrt{2} \).
- Ekvationen \( y = 3 \pm \sqrt{2-x^2} \) föreställer en cirkel. Bestäm mittpunkt och radie för cirkeln.
\( y = 3 \pm \sqrt{2-x^2} \) är samma som \( x^2 - (y-3)^2 = \pm 2 \).
Cirklens mittpunkt är \( (0,3) \) och radien är \( \sqrt{2} \).