4. Avstånd i koordinatsystem
Bestäm avståndet mellan \( (-3,-1) \) och \( (1,2) \).
Lösning
Sitationen är följande:
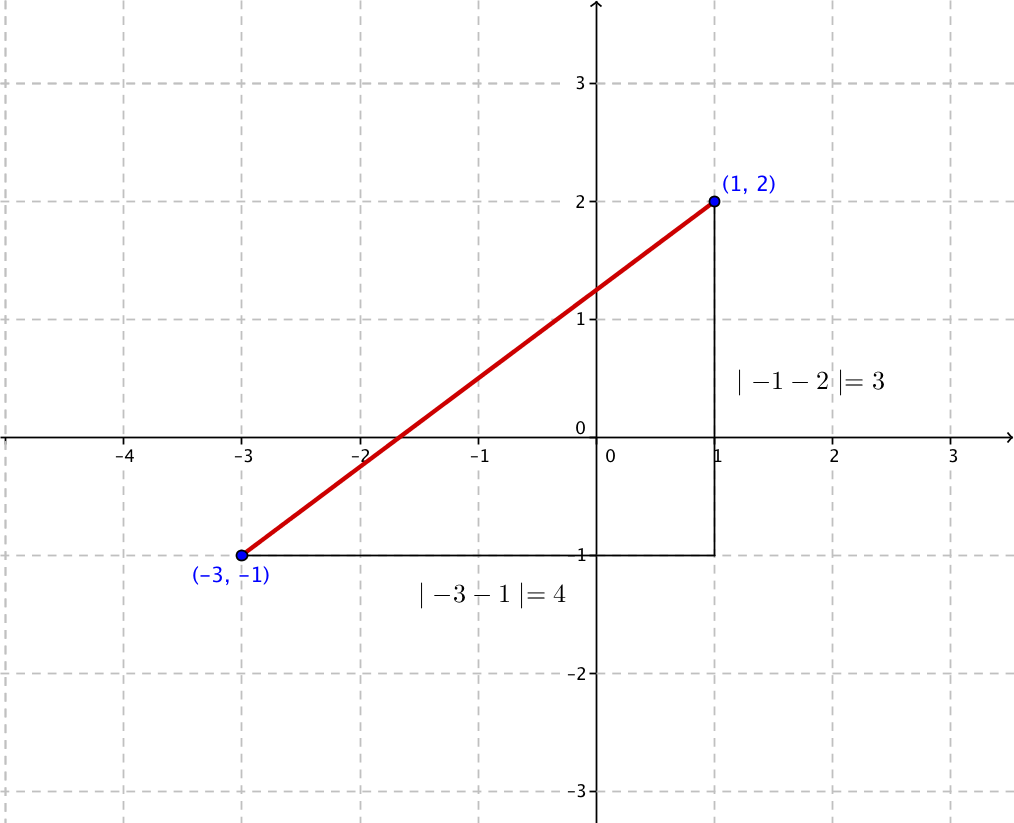
Vi får avståndet genom att tillämpa Pythagoras sats. Avstånden bestämmer vi som \( \mid -3 -1\mid = 4 \) och \( \mid -1-2\mid = 3 \). Avståndet blir \( \sqrt{4^2+3^2} = \sqrt{25}=5 \).
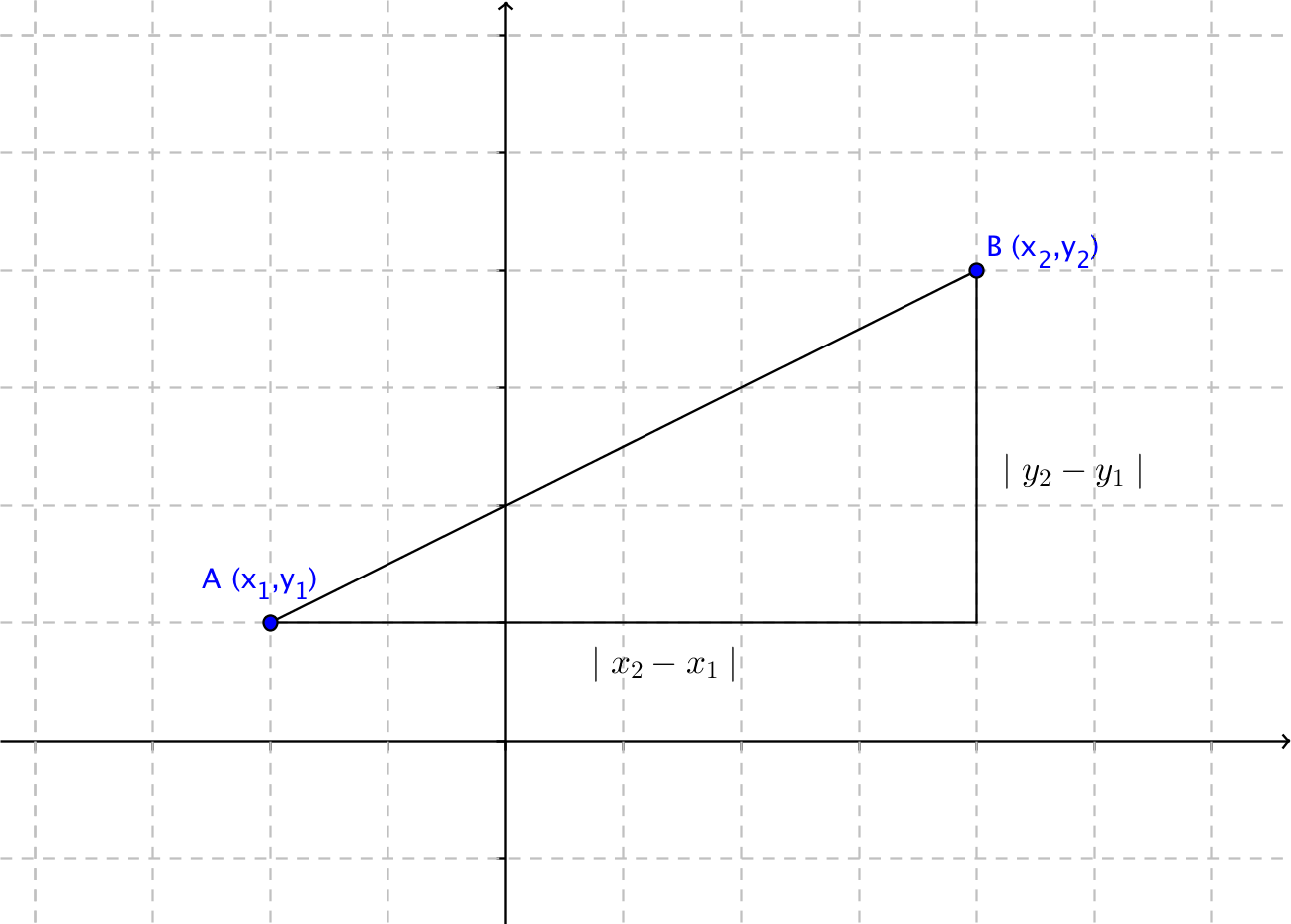
Allmänt gäller att vi tar två punkter \( A=(x_1,y_1) \) och \( B=(x_2,y_2) \). Avståndet, \( \mid AB \mid^2 \), får vi via \( \mid x_2-x_1 \mid ^2 + \mid y_2-y_1 \mid ^2 \), som vi skriver som \( \mid AB\mid ^2 = (x_2-x_1)^2+(y_2-y_1)^2 \) som är \( \mid AB \mid = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \) .
Exempel 1 Bestäm avståndet mellan \( (-4,1) \) och \( (6,-1) \).
Lösning
Avståndet är, \( \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} = \sqrt{(6-(-4))^2+(-1-1)^2} = 2\sqrt{26} \) l.e.
Exempel 2 Bestäm alla \( x \)-koordinater så att avståndet mellan \( (1,1) \) och \( (x,-4) \) är \( \sqrt{34} \).
Lösning
Vi ställer upp en ekvation. För avståndet, d, gäller
\( \begin{array}{rcll} d & = & \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ \sqrt{34} & = & \sqrt{(x-1)^2+(-4-1)^2} & \mid (\quad)^2\\ 34 & = & (x-1)^2+(-5)^2 \\ 34 & = & (x-1)^2+25 \\ (x-1)^2 & = & 34-25 & \end{array} \)
Om vi vill kan vi naturligtvis lösa denna ekvation med rotformeln.
\( \begin{array}{rcll} (x-1)^2 & = & 9 & \mid \sqrt{\quad} \\ x-1 & = & \pm 3 \\ x & = & \pm3 +1 \\ \end{array} \)
Punkterna är alltså \( (-2,-4) \) och \( (4,-4) \).
Avstånd på GeoGebra
Bestäm avståndet mellan \( A = (-2,1) \) och \( B = (6,-1) \) genom att utnyttja dig av GeoGebra.
Uppgifter
- Bestäm avståndet mellan följande punkter.
- \( (-1,2) \) och \( (-4,3) \).
Vi får \( \sqrt{(-1-(-4))^2+(2-3)^2} = \sqrt{10} \) l.e.
- \( (4,-5) \) och \( (4,1) \).
Vi får \( \sqrt{(4-4)^2+(-5-1)^2} = \sqrt{36}=6 \) l.e.
- \( (2,-4) \) och \( (-1,3) \).
Vi får \( \sqrt{(2-(-1))^2+(-4-3)^2} = \sqrt{58} \) l.e.
- \( (-1,2) \) och \( (-4,3) \).
- Bestäm avståndet från origo för följande punkter
- \( (5,6) \)
Avståndet är \( \sqrt{(5-0)^2+(6-0)^2} = \sqrt{61} \) l.e.
- \( (1,4) \)
Avståndet är \( \sqrt{(1-0)^2+(4-0)^2} = \sqrt{17} \). l.e.
- \( (-1,-3) \)
Avståndet är \( \sqrt{(-1-0)^2+(-3-0)^2} = \sqrt{10} \) l.e.
- \( (5,6) \)
- En triangels hörnpunkter är \( (5,-2) \), \( (4,2) \) och \( (-1,-1) \). Bestäm storleken av triangelns area.
Sitationen är följande
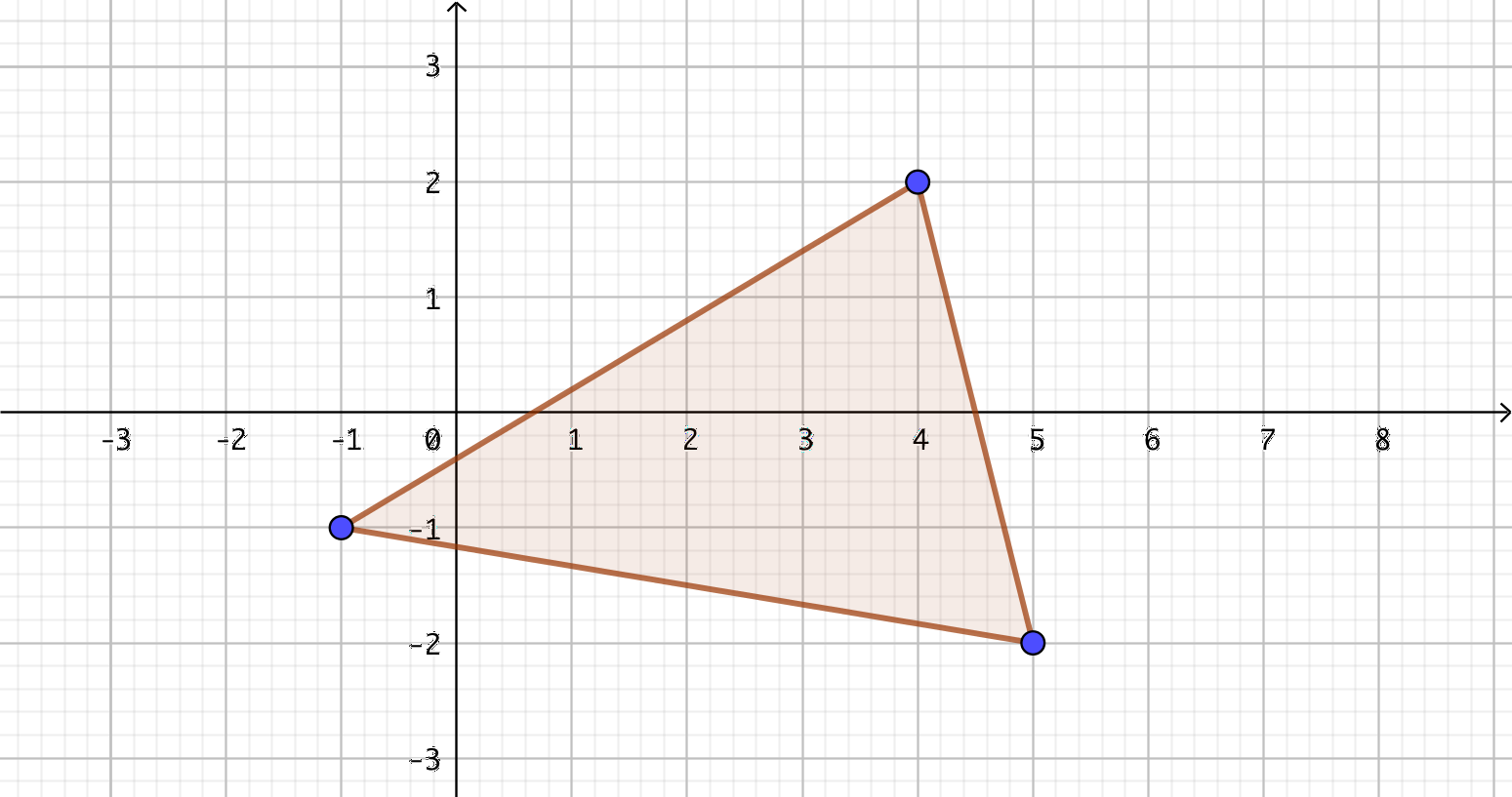
Eftersom vi inte ännu kan bestämma vinklar mellan linjer bestämmer vi storleken av rektangeln och tar bort arean av tre trianglar.
Rektangelns area är 24 a.e.
Trianglarnas areor är \( \dfrac{15}{2} \), 2 och 3 a.e.
Se till att du bestämmer, räknar dessa!
Den sökta triangelns area är 11,5 a.e.
- En fyrhörnings hörnpunkter är \( (4,4) \), \( (1,3) \), \( (2,-2) \) och \( (6,1) \). Bestäm storleken av fyrhörningens area.
Sitationen är följande
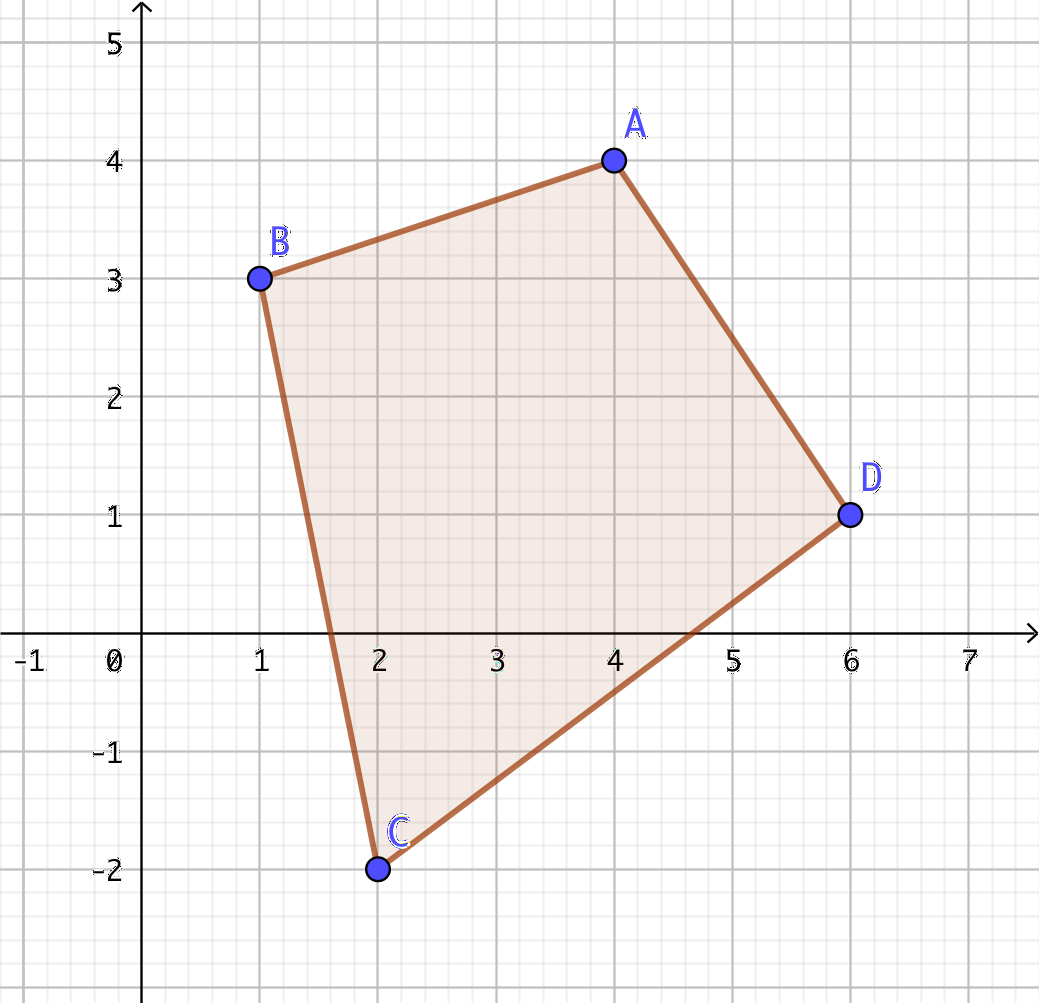
Vi bestämmer arean av rektangeln runt och subraherar arean av de fyra extra trianglarna.
Rektangelns area är 30 a.e.
Trianglarnas areor är \( \dfrac{3}{2} \), \( \dfrac{5}{2} \) 3 och 6 a.e.
Se till att du bestämmer, räknar dessa!
Den sökta triangelns area är 17 a.e.
- Skapa ett uttryck som anger avståndet mellan de punkter som är på x-axeln, \( (x,0) \), och punkten \( (2,3) \).
Avståndet mellan två punkter är \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
Vi får \( d = \sqrt{(2 - x_1)^2 + (3 - 0)^2} = \sqrt{(2 - x_1)^2 + 9} \).
- Bestäm de punkter på x-axlen som har avståndet 5 till punkten \( (2,3) \).
Från förra momentet fick vi \( d = \sqrt{(2 - x_1)^2 + (3 - 0)^2} = \sqrt{(2 - x_1)^2 + 9} \).
Avståndet skall vara 5.
Alltså \( 5 = \sqrt{(2 - x)^2 + 9} \). När vi förenklar får vi andragradsekvationen \( x^2 -4x -12 = 0 \). Ekvationen har rötterna \( x = -2 \) och \( x = 6 \).
Punkterna är \( (-2,0) \) och \( (6,0) \).
- Bestäm de punkter på x-axlen som har avståndet 5 till punkten \( (2,3) \).
- Bestäm de punkter på x-axeln som har avståndet 5 till punkten (5,4).
Då punkterna skall finnas på x-axeln betyder det att y-koordinaten har värdet 0.
Vi får ekvationen \( \sqrt{(5-x)^2+(4-0)^2} = 5 \). Ekvationen har lösningarna \( x=2 \) och \( x=8 \).
Punktern är (2,0) och (8,0).
- Hörnpunkterna för en triangel är \( A=(17,-6) \), \( B=(10,18) \) och \( C=(-5,-2) \). Visa att trianglen är likbent.
Om triangeln är likbent är längden av två sidor lika långa.
Avståndet \( \mid AB \mid = 25 \).
Avståndet \( \mid AC \mid = 10\sqrt{5} \approx 22,36 \).
Avståndet \( \mid BC \mid = 25 \).
Eftersom avståndena mellan AB och BC är lika långa är triangeln likbent.
- Hörnpunkterna för en triangel är \( A=(6,-2) \), \( B=(-2,2) \) och \( C=(-4,-2) \). Visa att trianglen är rätvinlig. I vilken punkt hittar vi den räta vinkeln?
Om triangeln är rätvinklig så gäller Pythagoras sats. Vi bestämmer avståndet mellan hörnpunkterna och undersöker om Pythagoras sats gäller
Avståndet \( \mid AB \mid = 4\sqrt{5} \approx 8,94 \).
Avståndet \( \mid AC \mid = 10 \).
Avståndet \( \mid BC \mid = 2\sqrt{5} \approx 4,47 \).
Den längsta sidan är 10, \( 10^2 = 100 \).
Vidare \( (4\sqrt{5})^2 + (2\sqrt{5})^2 = 16\cdot 5 + 4\cdot 5 = 100 \).
Alltså är triangeln rätvinklig.
Den räta vinkeln finns i punkten B.
- För punkten P:s koordinater gäller att x-koordinaten och y-koordinaten har samma värde. Bestäm koordinaten för P då P är på avståndet \( \sqrt{5} \) från punkten (0,-1).
Eftersom punkten P:s koordinater är lika stora kan vi skriva dem som (a,a).
Vi får ekvationen \( \sqrt{(a-0)^2+(a-(-1))^2} = \sqrt{5} \) som har lösningarna \( a=1 \) och \( a=-2 \).
Koordinaterna är (1,1) och (-2,-2).
- Bestäm sidans längd och arean för den kvadrat vars hörnpunkter är (-1,-2), (2,0), (0,3) och (-3,1).
Sidans längd är avståndet mellan två hörnpunkter på kvadraten, \( s = \sqrt{(-3-(-1))^2+(1-(-2))^2} = \sqrt{13} \).
Arean av en kvadrat är \( s^2 \), alltså \( (\sqrt{13})^2=13 \).