5. Geometriskt plan i rymden
Ett geometriskt plan kan vi bilda på 3 olika sätt. Vi kan utnyttja kryssprodukten mellan två vektorer och en punkt, vi kan jobba med tre punkter eller så har vi två vektorer som spänner upp planet.
Plan med hjälp av kryssprodukten
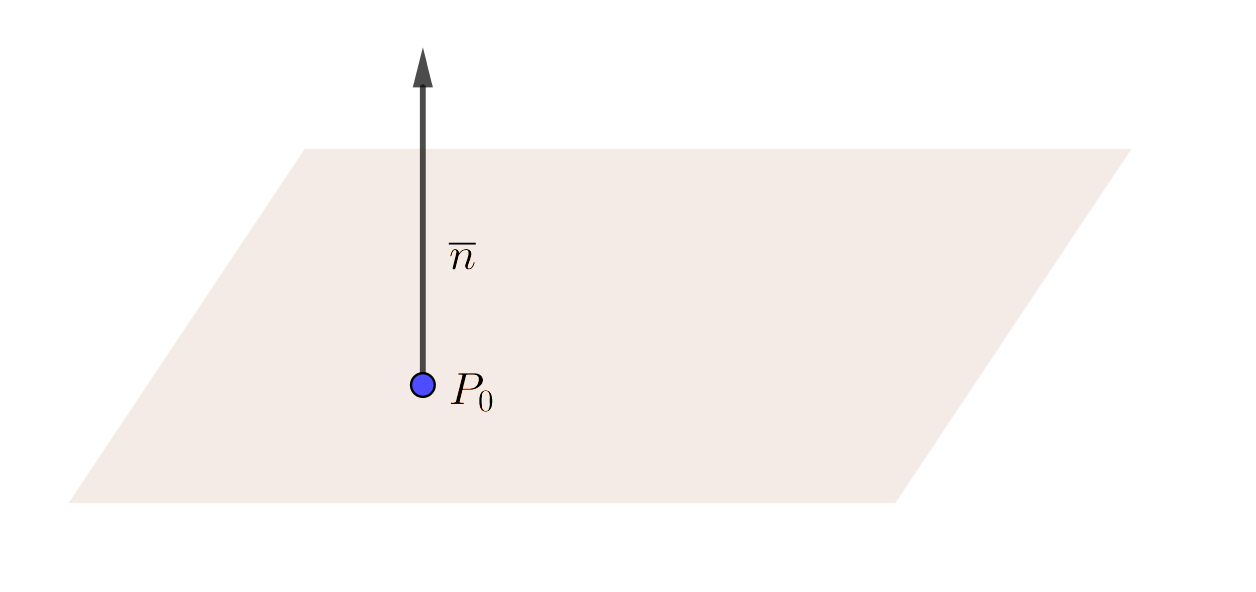
Då vi bildar kryssprodukten mellan två vektorer får vi en vektor \( \overline{n} = a\overline{i} +b\overline{j} +c\overline{k} \) som är vinkelrät mot det plan som vektorerna spänner upp. Med hjälp av \( \overline{n} \) och en punkt \( P_0 =(x_0, y_0, z_0) \) som är i planet får vi ekvationen för planet \( a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \).
Exempel 1 Bestäm ekvationen för det plan som är vinkelrät mot vektorn \( \overline{n} = -5\overline{j} + 3\overline{k} \) och som går genom punkten \( P =(1,-1,2) \).
Lösning
Vi utnyttjar ekvationen \( a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \) och får \( 0(x-1) + -5(y-(-1)) + 3(z-2) = 0 \). Detta är planets ekvation i koordinatform.
När vi förenklar får vi
\( \begin{array}{rcl} 0(x-1) + -5(y-(-1)) + 3(z-2) & = & 0 \\ -5y-5+3z-6 & = & 0 \\ -5y +3z - 11 & = & 0 \\ \end{array} \)
Planets ekvation är i normalform \( -5y +3z - 11 = 0 \).
Plan med hjälp av punkter och vektorer
Exempel 2 Är punkten \(P=(16,1,33)\) i planet som spänns upp av punkterna \((-1,2,-3)\), \((4,-5,2)\) och \((2,-1,1)\)?
Lösning
Vi skissar upp följande bild:
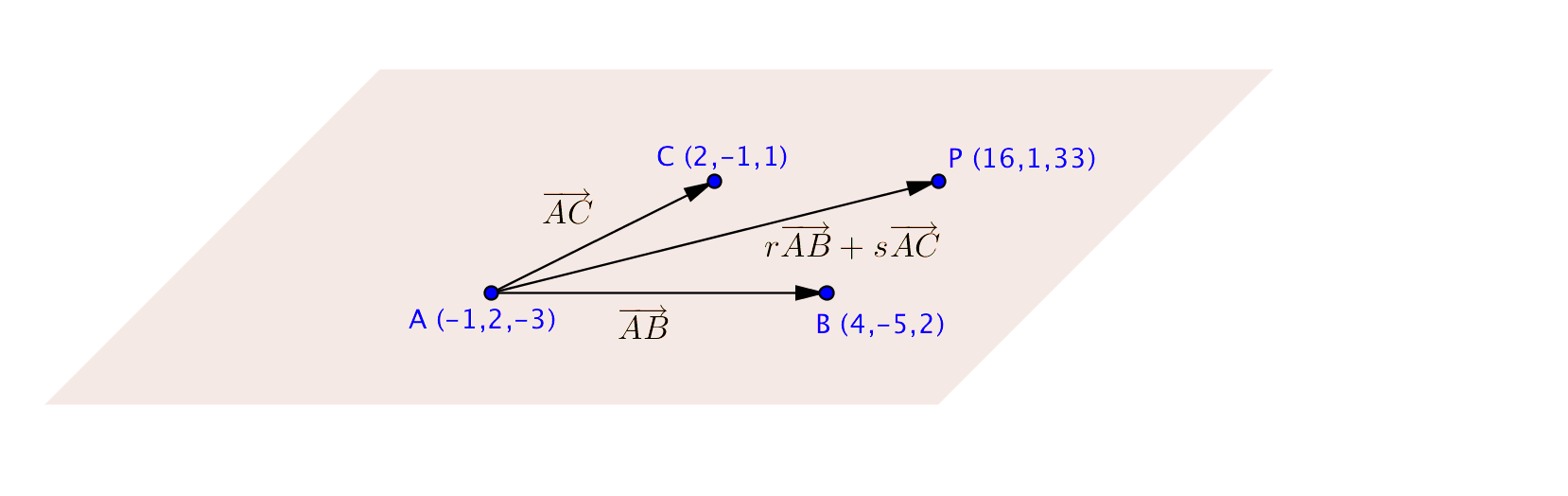
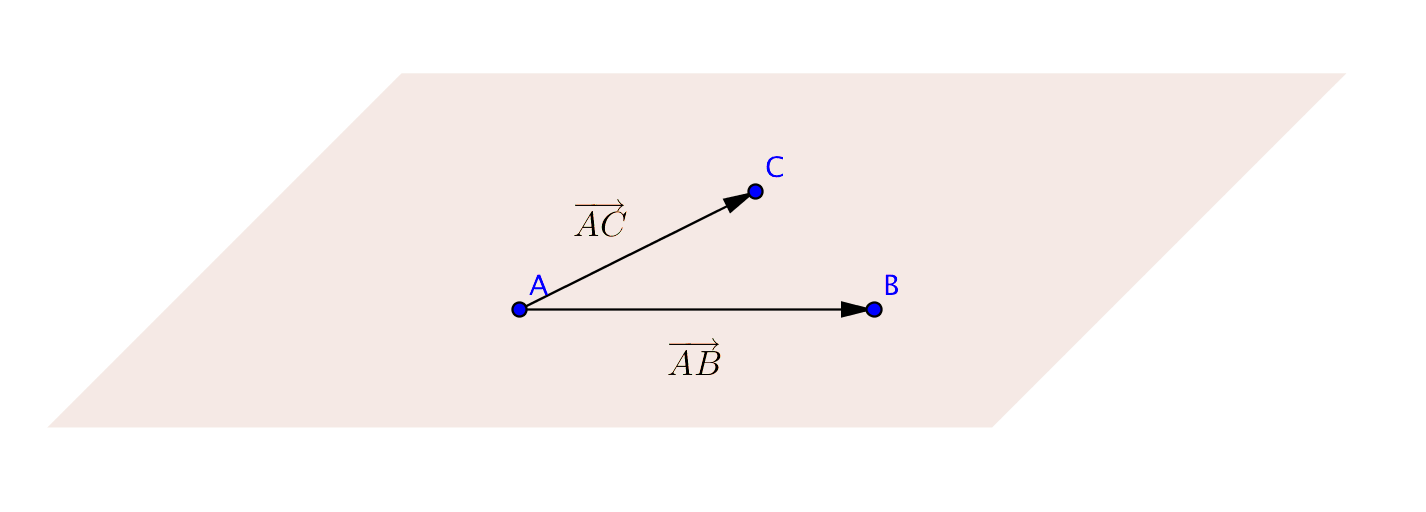
Om \(P\) ligger i planet så kan vi uttrycka \(\overrightarrow{AP}\) som komponenter av \(\overrightarrow{AB}\) och \(\overrightarrow{AC}\), alltså \(\overrightarrow{AP}=r\overrightarrow{AB}+s\overrightarrow{AC}\).
Vi bildar vektorerna,
\(\begin{array}{l} \overrightarrow{AP} = (16-(-1)\overline{i}+(1-2)\overline{j}+(33-(-3))\overline{k} = 17\overline{i}-\overline{j}+36\overline{k} \\ \overrightarrow{AB} = (4-(-1)\overline{i}+(-5-2)\overline{j}+(2-(-3))\overline{k} = 5\overline{i}-7\overline{j}+5\overline{k} \\ \overrightarrow{AC} = (2-(-1)\overline{i}+(-1-2)\overline{j}+(1-(-3))\overline{k} = 3\overline{i}-3\overline{j}+4\overline{k} \\ \end{array}\)
Vi får att:
\(\begin{array}{rcl} \overrightarrow{AP} &=& r\overrightarrow{AB}+s\overrightarrow{AC} \\ 17\overline{i}-\overline{j}+36\overline{k} &=& r[5\overline{i}-7\overline{j}+5\overline{k}]+s[3\overline{i}-3\overline{j}+4\overline{k}] \\ 17\overline{i}-\overline{j}+36\overline{k} &=& (5r+3s)\overline{i}+(-7r-3s)\overline{j}+(5r+4s)\overline{k} \\ \end{array}\)
Uppdelning i bas är entydig och vi får
\(\left\{ \begin{array}{rcl} 17 &=& 5r+3s \\ -1 &=&-7r-3s \\ 36&=& 5r+4s \\ \end{array} \right.\)
Den första och tredje ekvationen ger oss
\(\left\{ \begin{array}{rcl} 17 &=& 5r+3s \\ 36&=& 5r+4s \\ \end{array} \right.\)
som har lösningarna \(r=-8\) och \(s=19\). Då vi sätter in värdena i den andra ekvationen, \(-1 =-7r-3s = -7(-8)-3\cdot 19 = 56-57\) som stämmer. (Vi kan lösa hela ekvationssystemet med räknare och konstatera att ekvationerna satisfierar varandra.)
Vi kan alltså skriva \(\overrightarrow{AP}\) som komponenter av \(\overrightarrow{AB}\) och \(\overrightarrow{AC}\). Punkten \(P\) ligger alltså i planet.
Ett geometriskt plan spänns upp av en punkt A och basvektorerna \(\overline{u}\) och \(\overline{v}\). Om punkten P finns i planet kan vi uttrycka \(\overrightarrow{AP}\) som komponenter av \(\overline{u}\) och \(\overline{v}\), dvs \(\overrightarrow{AP}=r\overline{u}+s\overline{v}\) där \(r\) och \(s\) är reella tal.
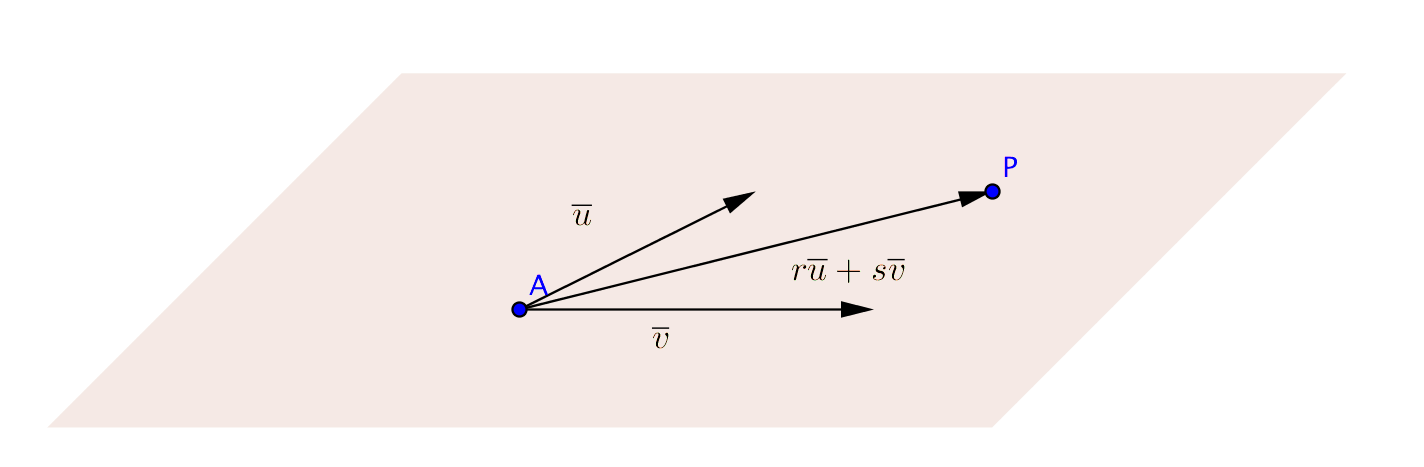
Utnyttjar vi ortsvektorerna \(\overrightarrow{OA}\) och \(\overrightarrow{OP}\) blir villkoret att \(\overrightarrow{OP}= \overrightarrow{OA} + r\overline{u}+s\overline{v}\) där \(r\) och \(s\) är reella tal.

Vi kallar detta för planets ekvation i parameterform.
Exempel 3 Ett plan går igenom punkten \((-1,2,1)\) och spänns upp av vektorerna \(\overline{u}= 5\overline{i}+\overline{j}+\overline{k}\) och \(\overline{v} = -\overline{i}-\overline{j}-2\overline{k}\). För vilka villkor gäller att punkten \(P=(x,y,z)\) är i planet? I vilken punkt skär planet x-axeln?
Lösning
Vi skissar upp följande bild:

Punkten \(P\) är i planet om villkoret \(\overrightarrow{OP}=\overrightarrow{OA}+r\overline{u}+s\overline{v}\) gäller.
\(\begin{array}{rcl} \overrightarrow{OP} &=& \overrightarrow{OA}+r\overline{u}+s\overline{v} \\ x \overline{i} + y \overline{j} + z \overline{k} &=& -\overline{i}+2\overline{j}+\overline{k}+r[5\overline{i}+\overline{j}+\overline{k}]+s[-\overline{i}-\overline{j}-2\overline{k}] \\ x\overline{i}+y\overline{j}+z\overline{k} &=& (-1+5r-s)\overline{i}+(2+r-s)\overline{j}+(1+r-2s)\overline{k} \\ \end{array}\)
För att \(x\), \(y\) och \(z\) skall vara i planet gäller att
\(\left\{ \begin{array}{rcl} x &=& -1+5r-s \\ y &=& 2+r-s \\ z &=& 1+r-2s \\ \end{array} \right.\)
för reella värden på \(r\) och \(s\).
Planet skär \(x\)-axeln då \(y=0\) och \(z=0\). Vi får att
\(\left\{ \begin{array}{rcl} 0 &=& 2+r-s \\ 0 &=& 1+r-2s \\ \end{array} \right.\)
som har lösningarna \(r=-3\) och \(s=-1\). De ger att \(x=-1+5(-3)-(-1)=-15\). Skärningspunkten är \((-15,0,0)\).
Uppgifter
- Bestäm ekvationen för det plan som är vinkelrätt mot vektorn \( n \) och som går genom punkten \( P \). Då
- \( \overline{n} = \overline{i} + 2\overline{j} -3\overline{k} \) och \( P =(2,1,0) \)
Vi jobbar med \( a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \) och får
\( \begin{array}{rcl} 1(x-2) + 2(y-1) -3(z-0) & = & 0 \\ x-2 +2y-2-3z & = & 0 \\ x +2y-3z -4 & = & 0 \\ \end{array} \)
- \( \overline{n} = 2\overline{i} -7\overline{j} +\overline{k} \) och \( P =(4,-2,-3) \)
Vi jobbar med \( a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \) och får
\( \begin{array}{rcl} 2(x-4) -7(y-(-2)) +(z-(-3)) & = & 0 \\ 2x-8 -7y-14 +z +3 & = & 0 \\ 2x -7y+z -19 & = & 0 \\ \end{array} \)
- \( \overline{n} = 3\overline{i} -2\overline{j} \) och \( P =(-1,5,-2) \)
Vi jobbar med \( a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 \) och får
\( \begin{array}{rcl} 3(x-(-1)) -2(y-5) +0(z-(-2)) & = & 0 \\ 3x+3 -2y+10 & = & 0 \\ 3x -2y +13 & = & 0 \\ \end{array} \)
- \( \overline{n} = \overline{i} + 2\overline{j} -3\overline{k} \) och \( P =(2,1,0) \)
- Lös följande uppgift med hjälp av kryssprodukten. Ett plan spänns upp av punkterna \((1,0,1)\), \((0,1,-1)\) och \((-1,-1,0)\). Är följande punkter i planet?
- \((3,2,1)\) .
Vi bildar vektorerna. Beroende på vilka punkter som vi väljer får vi lite olika basvektorer.
\( \overrightarrow{AB} = (0-1)\overline{i} + (1-0)\overline{j} + (-1-1)\overline{k} = -\overline{i}+\overline{j} -2\overline{k} \).
\( \overrightarrow{AC} = (-1-1)\overline{i} + (-1-0)\overline{j} + (0-1)\overline{k} = -2\overline{i}-\overline{j} -\overline{k}\).
Vi får \( \overline{AB} \times \overline{AC} = -3\overline{i} + 3\overline{j} + 3\overline{k} \).
Vi använder oss av punkten \( (1,0,1) \). Vi får planets ekvation som
\( \begin{array}{rcl} a(x-x_0) + b(y-y_0) + c(z-z_0) & = & 0 \\ -3(x-1) +3(y-0) +3(z-1) & = & 0 \\ -3x +3 +3y +3z -3 & = & 0 \\ -3x +3y +3z & = & 0 \\ \end{array} \)
Om punkten \( (3,2,1) \) är i planet skall ekvationen stämma.
\( -3\cdot 3 +3\cdot 2 +3\cdot 1 = -9+6+3 = 0 \).
Alltså är punkten i planet.
- \((5,2,2)\)
Vi utnyttjar ekvationen i föregående uppgift, \( -3x +3y +3z = 0 \).
Alltså \( -3\cdot 5 +3\cdot 2 +3\cdot 2 = -15+6+6 = -3 \).
Alltså är punkten inte i planet.
- \((3,2,1)\) .
- Lös följande uppgift med hjälp av basvektorer. Ett plan spänns upp av punkterna \((1,0,1)\), \((0,1,-1)\) och \((-1,-1,0)\). Är följande punkter i planet?
Bilda en ekvation för planet och testa om punkterna satisfierar ekvationen. Se vid behov exempel 1.
- \((3,2,1)\) .
Om punkten \( P=(3,2,1) \) är i planet som spänns upp av punkterna \( A=(1,0,1) , B=(0,1,-1) \) och \( C=(-1,-1,0) \) gäller ekvationen \( \overrightarrow{AP} = r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi bildar vekrorerna. Beroende på vilka punkter som vi väljer får vi lite olika basvektorer.
\( \overrightarrow{AB} = (0-1)\overline{i} + (1-0)\overline{j} + (-1-1)\overline{k} = -\overline{i}+\overline{j} -2\overline{k} \).
\( \overrightarrow{AC} = (-1-1)\overline{i} + (-1-0)\overline{j} + (0-1)\overline{k} = -2\overline{i}-\overline{j} -\overline{k}\).
\( \overrightarrow{AP} = (3-1)\overline{i} + (2-0)\overline{j} + (1-1)\overline{k} = 2\overline{i} +2\overline{j} \).
Vi får \( \overrightarrow{AP} = r\overrightarrow{AB} + s\overrightarrow{AC} \)
Då vi löser på kommer vi fram till ekvationssystemet
\( \left\{ \begin{array}{rcl} 2 & = & -r-2s \\ 2 & = & r - s \\ 0 & = & -2r -s \\ \end{array} \right. \)
Eftersom \( r = \dfrac{2}{3} \) och \( s = -\dfrac{4}{3} \) satisfierar alla tre ekvationer ligger punkten i planet.
- \((5,2,2)\)
Om punkten \( P = (5,2,2) \) är i planet som spänns upp av punkterna \( A=(1,0,1) , B=(0,1,-1) \) och \( C=(-1,-1,0) \) gäller ekvationen \( \overrightarrow{AP} = r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi bildar vekrorerna. Beroende på vilka punkter som vi väljer får vi lite olika basvektorer.
\( \overrightarrow{AB} = (0-1)\overline{i} + (1-0)\overline{j} + (-1-1)\overline{k} = -\overline{i}+\overline{j} -2\overline{k} \).
\( \overrightarrow{AC} = (-1-1)\overline{i} + (-1-0)\overline{j} + (0-1)\overline{k} = -2\overline{i}-\overline{j} -\overline{k}\).
\( \overrightarrow{AP} = (5-1)\overline{i} + (2-0)\overline{j} + (2-1)\overline{k} = 4\overline{i} +2\overline{j} +\overline{k} \).
Vi får \( \overrightarrow{AP} = r\overrightarrow{AB} + s\overrightarrow{AC} \)
Då vi löser på kommer vi fram till ekvationssystemet
\( \left\{ \begin{array}{rcl} 4 & = & -r-2s \\ 2 & = & r - s \\ 1 & = & -2r -s \\ \end{array} \right. \)
Eftersom ekvationssystemet saknar lösningar ligger punkten inte i planet.
- \((3,2,1)\) .
- I vilken punkt skär linjen som går genom origo och \((1,1,4)\) planet som spänns upp av \((1,3,-1)\), \((2,4,0)\) och \((1,5,3)\).
Vi börjar med att bilda planets ekvation.
\( A=(1,3,-1)\), \( B=(2,4,0)\) och \( C=(1,5,3)\).
\( \overrightarrow{AB} = (2-1)\overline{i} + (4-3)\overline{j} + (0-(-1))\overline{k} = \overline{i} + \overline{j} + \overline{k} \).
\( \overrightarrow{AC} = (1-1)\overline{i} + (5-3)\overline{j} + (3-(-1))\overline{k} = 2\overline{j} + 4\overline{k} \).
\( \overrightarrow{OA} = \overline{i} + 3\overline{j} - \overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcl} x & = & 1 + r \\ y & = & 3 + r +2s \\ z & = & -1 +r +4s \\ \end{array} \right. \)
Eftersom linjen går genom origo och genom punkten är dess riktningsvektor \( s = \overline{i} + \overline{j} + 4\overline{k} \).
Linjens ekvation är
\( \left\{ \begin{array}{rcl} x & = & t \\ y & = & t \\ z & = & 4t \\ \end{array} \right. \)
Vi söker den gemensamma punkten för planet och linjen.
\( \left\{ \begin{array}{rcl} t & = & 1 + r \\ t & = & 3 + r +2s \\ 4t & = & -1 +r +4s \\ \end{array} \right. \)
Vi får \( r = -3 \), \( s = -1 \) och \( t = -2 \).
Vi sätter in \( t = -2 \) i linjens ekvation. Vi får skärningspunkten \((-2,-2,-8)\).
- I vilken punkt skär planet som spänns upp av punkterna \((-2,1,-1)\), \((1,2,-2)\) och \((1,-2,1)\) \(x\)-axeln?
Vi börjar med att bilda planets ekvation.
\( A=(-2,1,-1)\), \( B=(1,2,-2)\) och \( C=(1,-2,1)\).
\( \overrightarrow{AB} = (1-(-2))\overline{i} + (2-1)\overline{j} + (-2-(-1))\overline{k} = 3\overline{i} + \overline{j} - \overline{k} \).
\( \overrightarrow{AC} = (1-(-2))\overline{i} + (-2-1)\overline{j} + (1-(-1))\overline{k} = 3\overline{i} -3\overline{j} + 2\overline{k} \).
\( \overrightarrow{OA} = -2\overline{i} + \overline{j} - \overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcl} x & = & -2 + 3r +3s \\ y & = & 1 + r -3s \\ z & = & -1 -r +2s \\ \end{array} \right. \)
Punkten på \( x \)-axeln är av typ \( (x,0,0) \).
Vi får ekvationssystemet
\( \left\{ \begin{array}{rcl} x & = & -2 + 3r +3s \\ 0 & = & 1 + r -3s \\ 0 & = & -1 -r +2s \\ \end{array} \right. \)
och får att \( r = -1\), \( s = 0\) och \( x = -5 \).
Punkten är \((-5,0,0)\).
- Punkterna \((-1,3,1)\), \((2,-2,1)\) och \((-1,-2,-1)\) spänner upp ett plan. Planet skär \(xy\)-planet i form av en linje. Bestäm linjens ekvation som formen \(Ax+By+C=0\).
Vi börjar med att bilda planets ekvation.
\( A=(-1,3,1)\), \( B=(2,-2,1)\) och \( C=(-1,-2,-1)\).
\( \overrightarrow{AB} = (2-(-1))\overline{i} + (-2-3)\overline{j} + (1-1)\overline{k} = 3\overline{i} -5 \overline{j} \).
\( \overrightarrow{AC} = (-1-(-1))\overline{i} + (-2-3)\overline{j} + (-1-1)\overline{k} = -5\overline{j} - 2\overline{k} \).
\( \overrightarrow{OA} = -\overline{i} + 3\overline{j} + \overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcl} x & = & -1 + 3r \\ y & = & 3 -5r-5s \\ z & = & 1 -2s \\ \end{array} \right. \)
De punkter som är i \( xy \)-planet är av typ \( (x,y,0) \).
Vi får ekvationssystemet
\( \left\{ \begin{array}{rcll} x & = & -1 + 3r & \Leftrightarrow r = \dfrac{x+1}{3} \\ y & = & 3 -5r-5s \\ 0 & = & 1 -2s & \Leftrightarrow s = \dfrac{1}{2}\\ \end{array} \right. \)
När vi sätter in värdena för \( r \) och \( s \) i den mittersta ekvationen får vi planets ekvation. Vi får \(10x+6y+7=0\).
Varje ekvation av formen \(Ax+By+Cz+D=0\) där \(A\), \(B\) eller \(C\) inte har värdet noll representerar ett plan. Detta kallas för planet ekvation i normalform. Ett sätt att skapa denna ekvation är att först skapa planets ekvation i parameterform och sedan eliminera \(r\) och \(s\).
Bestäm planets ekvation i normalform för det plan som spänns upp av
Bilda ett ekvationssystem där du har
\(\left\{\begin{array}{rcl} x & = & \ldots \\ y & = & \ldots \\ z & = & \ldots \\ \end{array}\right.\)
tag sedan och eliminera \(r\) och \(s\).
- \((0,0,0)\), \((1,0,3)\) och \((1,1,5)\).
Vi börjar med att bilda planets ekvation.
\( A=(0,0,0)\), \( B=(1,0,3)\) och \( C=(1,1,5)\).
\( \overrightarrow{AB} = (1-0)\overline{i} + (0-0)\overline{j} + (3-0)\overline{k} = \overline{i} + 3\overline{k} \).
\( \overrightarrow{AC} = (1-0)\overline{i} + (1-0)\overline{j} + (5-0)\overline{k} = \overline{i} +\overline{j} +5 \overline{k} \).
\( \overrightarrow{OA} = 0\overline{i} +0\overline{j} + 0\overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcll} x & = & r +s & \Leftrightarrow r = x-s\\ y & = & s \\ z & = & 3r +5s \\ \end{array} \right. \)
Vi kombinerar ekvationerna till en ekvation. Vi får planets ekvation \(3x+2y-z=0\).
- \((1,3,-1)\), \((2,4,1)\) och \((3,3,-2)\).
Vi börjar med att bilda planets ekvation.
\( A=(1,3,-1)\), \( B=(2,4,1)\) och \( C=(3,3,-2)\).
\( \overrightarrow{AB} = (2-1)\overline{i} + (4-3)\overline{j} + (1-(-1))\overline{k} = \overline{i} +\overline{j} + 2\overline{k} \).
\( \overrightarrow{AC} = (3-1)\overline{i} + (3-3)\overline{j} + (-2-(-1))\overline{k} = 2\overline{i} - \overline{k} \).
\( \overrightarrow{OA} = \overline{i} +3\overline{j} -\overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcll} x & = & 1+ r +2s \\ y & = & 3+r & \Leftrightarrow r = y-3\\ z & = & -1 +2r -s & \Leftrightarrow s = -1+2r-z \\ \end{array} \right. \)
Vi kombinerar ekvationerna till en ekvation. Vi får planets ekvation \( x-5y+2z+16=0\).
- \((-2,0,1)\), \((-1,2,-1)\) och \((1,1,-4)\).
Vi börjar med att bilda planets ekvation.
\( A=(-2,0,1)\), \( B=(-1,2,-1)\) och \( C=(1,1,-4)\).
\( \overrightarrow{AB} = (-1-(-2))\overline{i} + (2-0)\overline{j} + (-1-1)\overline{k} = \overline{i} + 2\overline{j} - 2\overline{k} \).
\( \overrightarrow{AC} = (1-(-2))\overline{i} + (1-0)\overline{j} + (-4-1)\overline{k} = 3\overline{i} +\overline{j} -5 \overline{k} \).
\( \overrightarrow{OA} = -2\overline{i} + \overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcll} x & = & -2 + r +3s & \Leftrightarrow r = x+2-3s\\ y & = & 2r +s & \Leftrightarrow s = y-2r \\ z & = & 1 -2r -5s \\ \end{array} \right. \)
Vi får planets ekvation \(8x-y-5z-11=0\).
- \((1,-1,-2)\), \((0,3,1)\) och \((3,-2,-1)\)
Vi börjar med att bilda planets ekvation.
\( A=(1,-1,-2)\), \( B=(0,3,1)\) och \( C=(3,-2,-1)\).
\( \overrightarrow{AB} = (0-1)\overline{i} + (3-(-1))\overline{j} + (1-(-2))\overline{k} = -\overline{i} + 4\overline{j} + 3\overline{k} \).
\( \overrightarrow{AC} = (3-1)\overline{i} + (-2-(-1))\overline{j} + (-1-(-2))\overline{k} = 2\overline{i} -\overline{j} + \overline{k} \).
\( \overrightarrow{OA} = \overline{i} - \overline{j} -2\overline{k} \).
Punkten \( P \) har koordinaterna P \( (x,y,z) \).
Vi bildar \( \overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC} \).
Vi kommer fram till planets ekvation
\( \left\{ \begin{array}{rcll} x & = & 1 - r +2s & (1.)\\ y & = & -1 +4r -s & (2.) \\ z & = & -2 +3r +s & (3.) \\ \end{array} \right. \)
Då vi kombinerar ekvationerna får vi planets ekvation, \(x+y-z-2=0\)
- \((0,0,0)\), \((1,0,3)\) och \((1,1,5)\).