4. Kryssprodukt av vektorer
Tidigare har vi multiplicerat reella tal med vektorer och bildat skalära produkten mellan två vektorer. Till nästa tar vi och jobbar med något som kallas för kryssprodukt. Du kan tänka det som att vi multiplicerar två vektorer med varandra. Kryssprodukten fungerar för vissa rum, 3 och 7 dimensionella. Här jobbar vi med kryssprodukten i 3 dimensioner.
När vi bildar kryssprodukten mellan två tredimensionella vektorer, \( \overline{a} \times \overline{b} \), får vi en ny tredimensionell vektor. Som alla vektorer har kryssproduktsvektorn längd och riktning, och den är vinkelrät mot det plan som vektoerna \( \overline{a} \) och \( \overline{b} \) bildar.

I bilden ovan ger kryssprodukten av \( \overline{a} \times \overline{b} \) storleken av arean för parallellogrammen som bildas.
Kryssprodukten används bland annat i rörelsemängd- och vridmoment och då laddade partiklar färdas i magnetfält.
Kryssprodukten mellan vektorerna \( \overline{a} = a_x\overline{i} + a_y\overline{j} + a_z\overline{j} \) och \( \overline{b} = b_x\overline{i} + b_y\overline{j} + b_z\overline{j} \) är vektors vars determinant är \( \begin{vmatrix} \overline{i} & \overline{j} & \overline{j} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{vmatrix} \).
Hur vi bestämmer determinanten kommer fram nedan och i MAOL.
En \( 3 \times 3 \)-determinant bottar sig i en \( 2 \times 2 \)-determinant. Vi börjar med att bestämma en \(2 \times 2\)-determinant. Determinanten för en tvårandig, \(2 \times 2\), är \( \begin{vmatrix} a & b \\ c & d \\ \end{vmatrix} = ad - bc \).
För en trerandig determinant, \(3 \times 3 \), gäller följande: \( \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{vmatrix} = a \begin{vmatrix} e & f \\ h & i \end{vmatrix} -b \begin{vmatrix} d & f \\ g & i \end{vmatrix} +c \begin{vmatrix} d & e \\ g & h \end{vmatrix} \).
Märk att här finns en logik hur vi väljer värdena. För \( a \) bildar vi determinanten av de värden som inte är under \( a \), motsvarande gäller för \( b \) och \( c \).
Exempel 1 Bestäm kryssprodukten för vektorerna \( \overline{a} = \overline{i} + 3\overline{j} + 2\overline{j} \) och \( \overline{b} = -\overline{i} + 2\overline{j} + \overline{j} \).
Lösning
Vi får
\( \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 1 & 3 & 2 \\ -1 & 2 & 1 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} 3 & 2 \\ 2 & 1 \end{vmatrix} -\overline{j} \begin{vmatrix} 1 & 2 \\ -1 & 1 \end{vmatrix} +\overline{k} \begin{vmatrix} 1 & 3 \\ -1 & 2 \end{vmatrix} \\ = \overline{i}(3 \cdot 1 -2 \cdot 2) - \overline{j}(1 \cdot 1 -2 \cdot (-1)) + \overline{k}(1 \cdot 2 -3 \cdot (-1)) \\ = -1\overline{i} -3\overline{j} + 5\overline{k} \)
Då vi bilar kryssprodukten mellan två vektor är den tredje vektorn som uppstår vinkelrät mot planet som vektorerna spänner upp.
Vi jobbar med \( \overline{a} = a_x\overline{i} + a_y\overline{j} + a_z\overline{j} \) och \( \overline{b} = b_x\overline{i} + b_y\overline{j} + b_z\overline{j} \). Kryssprodukten är
\( \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \\ \end{vmatrix} = \overline{i} \begin{vmatrix} a_y & a_z \\ b_y & b_z \end{vmatrix} -\overline{j} \begin{vmatrix} a_x & a_z \\ b_x & b_z \end{vmatrix} +\overline{k} \begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix} \\ = \overline{i}(a_y b_z -a_z b_y) - \overline{j}(a_x b_z -a_z b_x) + \overline{k}(a_x b_y -a_y b_x) \\ \)
Det är samma som \( \overline{i}(a_y b_z -a_z b_y) +\overline{j}(-a_x b_z +a_z b_x) + \overline{k}(a_x b_y -a_y b_x) \)
Sedan bildar vi skalära produkten för
\( \begin{array}{rcl} (\overline{a} \times \overline{b}) \cdot \overline{a} & = & (a_y b_z -a_z b_y)a_x +(-a_x b_z +a_z b_x)a_y + (a_x b_y -a_y b_x)a_z \\ & = & a_x a_y b_z -a_x a_z b_y -a_x a_y b_z +a_y a_z b_x + a_x a_z b_y -a_y a_z b_x \\ & = & 0 \\ \end{array} \)
Alltså är vektorerna vinkelräta mot varandra.
Att \( \overline{a} \times \overline{b} \) är vinkelrät mot \( \overline{b} \) kan vi visa på motsvarande sätt.
Exempel 2 Bestäm en vektor som är vinkelrät mot vektorerna \( \overline{a} = -2\overline{i} - 3\overline{j} + \overline{j} \) och \( \overline{b} = -\overline{i} + \overline{j} +3\overline{j} \).
Lösning
Vi får
\( \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ -2 & -3 & 1 \\ -1 & 1 & 3 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} -3 & 1 \\ 1 & 3 \end{vmatrix} -\overline{j} \begin{vmatrix} -2 & 1 \\ -1 & 3 \end{vmatrix} +\overline{k} \begin{vmatrix} -2 & -3 \\ -1 & 1 \end{vmatrix} \\ = \overline{i}((-3) \cdot 3 -1 \cdot 1) - \overline{j}((-2) \cdot 3 -1 \cdot (-1)) + \overline{k}((-2) \cdot 1 -(-3) \cdot (-1)) \\ = -10\overline{i} +5\overline{j} - 5\overline{k} \)
En vektor är \( -10\overline{i} +5\overline{j} - 5\overline{k} \). Resten är multiplar av vektorn.
Exempel 3 Vektorerna \( \overline{a} = 2\overline{i} + \overline{j} \) och \( \overline{b} = 3\overline{i} -\overline{j} \) utgör sidorna i en parallellogram. Bestäm arean av parallellogrammen med hjälp av kryssprodukten.
Lösning
Vi tar och ritar vektorerna på Geogebra.
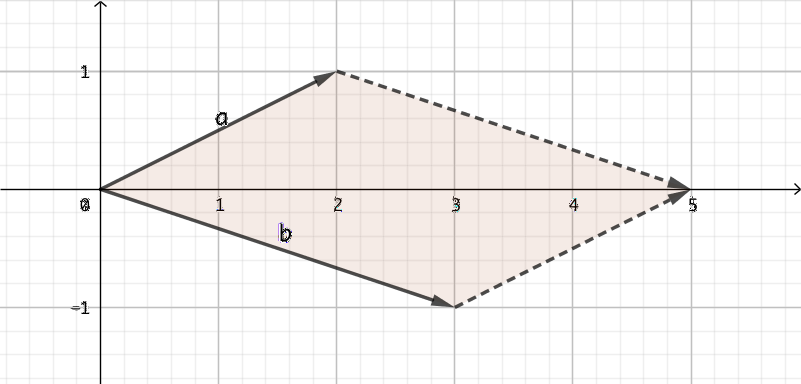
Längden av kryssprodukten ger arean av parallellogrammen, \( \mid \overline{a} \times \overline{b} \mid \).
Kryssprodukten har värdet \( \overline{a} \times \overline{b} = -5\overline{k} \).
Storleken av arean är \( \mid \overline{a} \times \overline{b} \mid = \sqrt{(-5)^2} = 5 \) a.e.
Uppgifter
- Bilda följande kryssprodukter för hand och kontrollera din lösning på CAS.
- \( \overline{a} \times \overline{b} \) då \( \overline{a} = 2\overline{i} -\overline{j} +2\overline{k} \) och \( \overline{b} = \overline{i} -2\overline{j} -3\overline{k} \).
Vi får
\( \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 2 & -1 & 2 \\ 1 & -2 & -3 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} -1 & 2 \\ -2 & -3 \end{vmatrix} -\overline{j} \begin{vmatrix} 2 & 2 \\ 1 & -3 \end{vmatrix} +\overline{k} \begin{vmatrix} 2 & -1 \\ 1 & -2 \end{vmatrix} \\ = \overline{i}(-1 \cdot (-3) -2 \cdot (-2)) - \overline{j}(2 \cdot (-3) -2 \cdot 1) + \overline{k}(2 \cdot (-2) -(-1) \cdot 1) \\ = 7\overline{i} +8\overline{j} -3\overline{k} \)
På GeoGebra

- \( \overline{b} \times \overline{a} \) då \( \overline{a} = 2\overline{i} -\overline{j} +2\overline{k} \) och \( \overline{b} = \overline{i} -2\overline{j} -3\overline{k} \).
Vi får
\( \overline{b} \times \overline{a} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 1 & -2 & -3 \\ 2 & -1 & 2 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} -2 & -3 \\ -1 & 2 \\ \end{vmatrix} -\overline{j} \begin{vmatrix} 1 & -3 \\ 2 & 2 \\ \end{vmatrix} +\overline{k} \begin{vmatrix} 1 & -2 \\ 2 & -1 \\ \end{vmatrix} \\ = \overline{i}(-2 \cdot 2 -(-3) \cdot (-1)) - \overline{j}(1 \cdot 2 -(-3) \cdot 2) + \overline{k}(1 \cdot (-1) -(-2) \cdot 2) \\ = -7\overline{i} -8\overline{j} +3\overline{k} \)
På GeoGebra

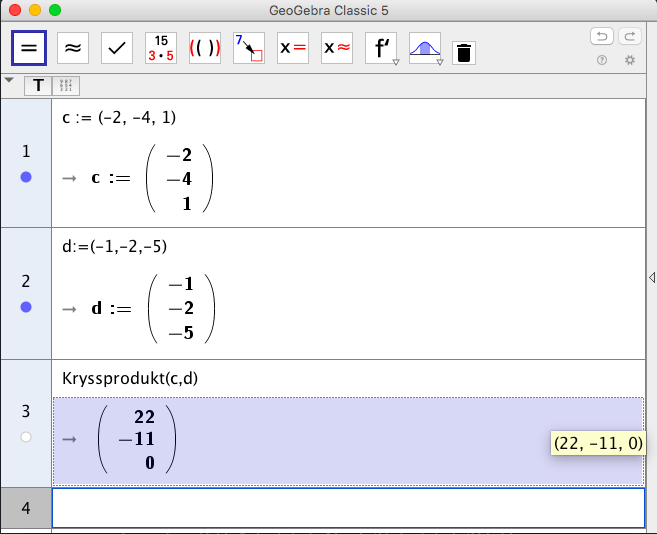
- \( \overline{c} \times \overline{d} \) då \( \overline{c} = -2\overline{i} -4\overline{j} +\overline{k} \) och \( \overline{d} = -\overline{i} -2\overline{j} -5\overline{k} \).
Vi får
\( \overline{c} \times \overline{d} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ -2 & -4 & 1 \\ -1 & -2 & -5 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} -4 & 1 \\ -2 & -5 \\ \end{vmatrix} -\overline{j} \begin{vmatrix} -2 & 1 \\ -1 & -5 \\ \end{vmatrix} +\overline{k} \begin{vmatrix} -2 & -4 \\ -1 & -2 \\ \end{vmatrix} \\ = \overline{i}(-4 \cdot (-5) -1 \cdot (-2)) - \overline{j}(-2 \cdot (-5) -1 \cdot (-1)) + \overline{k}(-2 \cdot (-2) -(-4) \cdot (-1)) \\ = 22\overline{i} -11\overline{j} \)
På GeoGebra
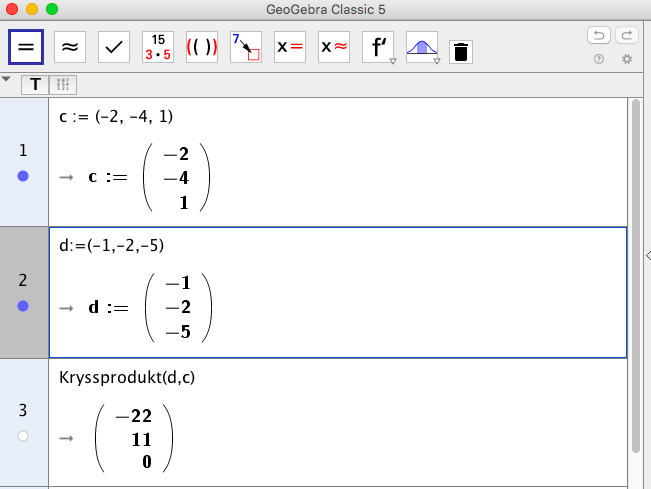
- \( \overline{d} \times \overline{c} \) då \( \overline{c} = -2\overline{i} -4\overline{j} +\overline{k} \) och \( \overline{d} = -\overline{i} -2\overline{j} -5\overline{k} \).
Vi får
\( \overline{d} \times \overline{c} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ -1 & -2 & -5 \\ -2 & -4 & 1 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} -2 & -5 \\ -4 & 1 \\ \end{vmatrix} -\overline{j} \begin{vmatrix} -1 & -5 \\ -2 & 1 \\ \end{vmatrix} +\overline{k} \begin{vmatrix} -1 & -2 \\ -2 & -4 \\ \end{vmatrix} \\ = \overline{i}(-2 \cdot 1 -(-5) \cdot (-4)) - \overline{j}(-1 \cdot 1 -(-5) \cdot (-2)) + \overline{k}(-1 \cdot (-4) -(-2) \cdot (-2)) \\ = -22\overline{i} +11\overline{j} \)
På GeoGebra
- Vad märker du då du bildar \( \overline{a} \times \overline{b} \) och \( \overline{b} \times \overline{a} \) och då du bildar \( \overline{c} \times \overline{d} \) och \( \overline{d} \times \overline{c} \)
Då vi bildar \( \overline{a} \times \overline{b} \) och \( \overline{b} \times \overline{a} \) får de motsatta vektorerna. Samma gäller för \( \overline{c} \times \overline{d} \) och \( \overline{d} \times \overline{c} \).
- \( \overline{a} \times \overline{b} \) då \( \overline{a} = 2\overline{i} -\overline{j} +2\overline{k} \) och \( \overline{b} = \overline{i} -2\overline{j} -3\overline{k} \).
- Låt \( \overline{a} = 2\overline{i}+\overline{j} \), \( \overline{b} = -3\overline{i}+2\overline{j} \) och \( \overline{c} = -\overline{i}-2\overline{k} \). Bilda följande kryssprodukter för hand och rita vektorerna i GeoGebra.
- \( \overline{a} \times \overline{b} \)
Vi får
\( \overline{a} \times \overline{b} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 2 & 1 & 0 \\ -3 & 2 & 0 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} 1 & 0 \\ 2 & 0 \\ \end{vmatrix} -\overline{j} \begin{vmatrix} 2 & 0 \\ -3 & 0 \\ \end{vmatrix} +\overline{k} \begin{vmatrix} 2 & 1 \\ -3 & 2 \\ \end{vmatrix} \\ = \overline{i}(1 \cdot 0 -0 \cdot 2) - \overline{j}(2 \cdot 0 -0 \cdot (-3)) + \overline{k}(2 \cdot 2 -1 \cdot (-3)) \\ = 7\overline{k} \)
På GeoGebra

- \( \overline{a} \times \overline{a} \)
Vi får
\( \overline{a} \times \overline{a} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ 2 & 1 & 0 \\ 2 & 1 & 0 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} 1 & 0 \\ 1 & 0 \\ \end{vmatrix} -\overline{j} \begin{vmatrix} 2 & 0 \\ 2 & 0 \\ \end{vmatrix} +\overline{k} \begin{vmatrix} 2 & 1 \\ 2 & 1 \\ \end{vmatrix} \\ = \overline{i}(1 \cdot 0 -0 \cdot 1) - \overline{j}(2 \cdot 0 -0 \cdot 2) + \overline{k}(2 \cdot 2 -1 \cdot 2) \\ = \overline{0} \)
Vi får en nollvektor.
På GeoGebra

- \( \overline{b} \times \overline{c} \)
Vi får
\( \overline{b} \times \overline{c} = \begin{vmatrix} \overline{i} & \overline{j} & \overline{k} \\ -3 & 2 & 0 \\ -1 & 0 & -2 \\ \end{vmatrix} = \overline{i} \begin{vmatrix} 2 & 0 \\ 0 & -2 \\ \end{vmatrix} -\overline{j} \begin{vmatrix} -3 & 0 \\ -1 & -2 \\ \end{vmatrix} +\overline{k} \begin{vmatrix} -3 & 2 \\ -1 & -2 \\ \end{vmatrix} \\ = \overline{i}(2 \cdot (-2) -0 \cdot 0) - \overline{j}(-3 \cdot (-2) -0 \cdot (-1)) + \overline{k}((-3) \cdot (-2) -2 \cdot (-1)) \\ = -4\overline{i} -6\overline{j} +2\overline{k} \)
På GeoGebra

- \( \overline{a} \times \overline{b} \)
- Bestäm en vektor som är vinkelrät till följande vektorer.
- \( \overline{a} = \overline{i} -2\overline{j} -5\overline{k} \) och \( \overline{b} = \overline{i} +\overline{k} \)
Kryssprodukten har värdet \( \overline{a} \times \overline{b} = -2\overline{i} -6\overline{j} +2\overline{k} \). Dessutom har vi multiplar av kryssprodukten.
- \( \overline{c} = -5\overline{j} -\overline{k} \) och \( \overline{d} = -3\overline{i} + 2\overline{j} -3\overline{k} \)
Kryssprodukten har värdet \( \overline{c} \times \overline{d} = 17\overline{i} +3\overline{j} -15\overline{k} \). Dessutom har vi multiplar av kryssprodukten.
- \( \overline{u} = \overline{k} \) och \( \overline{v} = -2\overline{j} +3\overline{k} \)
Kryssprodukten har värdet \( \overline{u} \times \overline{v} = 2\overline{i} \). Dessutom har vi multiplar av kryssprodukten.
- \( \overline{a} = \overline{i} -2\overline{j} -5\overline{k} \) och \( \overline{b} = \overline{i} +\overline{k} \)
- Bestäm arean av parallellogrammen som bildas av vektorerna \( \overline{a} = 3\overline{i} -\overline{j} \) och \( \overline{b} = \overline{i} +2\overline{j} \).
Kryssprodukten \( \overline{a} \times \overline{b} = 7\overline{k} \). Arean för parallellogrammen är 7 a.e.
- Bestäm arean av parallellogrammen som bildas av vektorerna \( \overline{a} = -\overline{i} -2\overline{j} -\overline{k} \) och \( \overline{b} = -3\overline{i} -\overline{j} +\overline{k} \).
Kryssprodukten \( \overline{a} \times \overline{b} = -3\overline{i} +4\overline{j} -5\overline{k} \).
Arean för parallellogrammen är \( \mid \overline{a} \times \overline{b} \mid = \sqrt{(-3)^2+4^2+(-5)^2} = 5\sqrt{2} \) a.e.
- Bestäm arean av parallellogrammen som bildas av vektorerna \( \overline{a} = 2\overline{i} -2\overline{j} -3\overline{k} \) och \( \overline{b} = -\overline{i} +3\overline{j} -\overline{k} \).
Kryssprodukten \( \overline{a} \times \overline{b} = -11\overline{i} +5\overline{j} +4\overline{k} \).
Arean för parallellogrammen är \( \mid \overline{a} \times \overline{b} \mid = \sqrt{11^2+5^2+4^2} = 9\sqrt{2} \) a.e.
- En triangel spänns upp av vektorerna \( \overline{a} = \overline{i} +3\overline{j} \) och \( \overline{b} = 2\overline{i} +\overline{j} \) och differensen av \( \overline{a} \) och \( \overline{b} \). Bestäm arean av triangeln.
Hur förhåller sig triangelns area till paralellogrammens area?
Triangelns area är hälften av paralellogrammens area.
Kryssprodukten \( \overline{a} \times \overline{b} = -5\overline{k} \).
Arean för parallellogrammen är \( \mid \overline{a} \times \overline{b} \mid = \sqrt{(-5)^2} = 5 \) a.e.
Då är arean för triangeln \( \dfrac{5}{2} \) a.e.
- En triangel bestäms av punkterna \( A=(3,1,4) \), \( B=(-1,2,1) \) och \( C = (-2,3,4) \). Bestäm arean för triangeln.
Vi jobbar med vektorerna \( \overline{AB} = -4\overline{i} +\overline{j} -3\overline{k} \) och \( \overline{AC} = -5\overline{i} +2\overline{j} \).
Vi får att \( \overline{AB} \times \overline{AC} = 6\overline{i} +15\overline{j} -3\overline{k} \).
Längden av \( \mid \overline{AB} \times \overline{AC} \mid = 3\sqrt{30} \).
Arean av triangeln \( ABC \) är \( \dfrac{3\sqrt{30}}{2} \) a.e.
- Hörnpunkterna av en triangel är \( (-3,4,5) \), \( (-1,4,-7) \) och \( (-4,0,3) \). Bestäm arean för triangeln.
Betecknar punkterna \( A=(-3,4,5) \), \( B=(-1,4,-7) \) och \( C=(-4,0,3) \)
Vi jobbar med vektorerna \( \overline{AB} = 2\overline{i} +12\overline{k} \) och \( \overline{AC} = -\overline{i} -4\overline{j} -2\overline{k} \).
Vi får att \( \overline{AB} \times \overline{AC} = -48\overline{i} +16\overline{j} -8\overline{k} \).
Längden av \( \mid \overline{AB} \times \overline{AC} \mid = 8\sqrt{41} \).
Arean av triangeln \( ABC \) är \( 4\sqrt{41} \) a.e.
- Bestäm storleken av den största vinkeln i triangeln.
Den största vinkeln hittar vi mot den längsta sidan.
Vi får att \( \overline{AB} = 2\overline{i} +12\overline{k} \). Längden är \( 2\sqrt{37} \approx 12,2 \) l.e.
\( \overline{AC} = -\overline{i} -4\overline{j} -2\overline{k} \). Längden är \( \sqrt{21} \approx 4,6 \) l.e.
\( \overline{BC} = -3\overline{i} -4\overline{j} +10\overline{k} \). Längden är \( 5\sqrt{5} \approx 11,2 \) l.e.
Alltså är den störsa vinkeln mot sidan \( AB \).
Storleken av vinkeln är 91,1o. (Använd dig av skalära produkten och vinklar mellan vektoer.)
- Bestäm storleken av den största vinkeln i triangeln.
- I teoridelen visade vi att \( \overline{a} \times \overline{b} \) är vinkelrät mot \( \overline{a} \). Visa att \( \overline{a} \times \overline{b} \) är vinkelrät mot \( \overline{b} \).
I teoridelen får vi att \( \overline{a} \times \overline{b} = \overline{i}(a_y b_z -a_z b_y) +\overline{j}(-a_x b_z +a_z b_x) + \overline{k}(a_x b_y -a_y b_x) \)
Sedan bildar vi skalära produkten för
\( \begin{array}{rcl} (\overline{a} \times \overline{b}) \cdot \overline{b} & = & (a_y b_z -a_z b_y)b_x +(-a_x b_z +a_z b_x)b_y + (a_x b_y -a_y b_x)b_z \\ & = & a_y b_x b_z -a_z b_x b_y -a_x b_y b_z +a_z b_x b_y + a_x b_y b_z -a_y b_x b_z \\ & = & 0 \\ \end{array} \)
Alltså är vektorerna vinkelräta mot varandra.