11. Repetition

Sedan är det bara att repetera.

Uppgifter

Bestäm en riktningsvektor för följande linjer.
1. $y = 4x-2$
  
  Då riktningskoefficenten är 4 rör vi oss 1 steg åt höger och 4 steg uppåt.
  
  En riktningsvektor är $\overline{s} = \overline{i} + 4\overline{j}$ .
  
  En annan är $\overline{s} = -\overline{i} -4\overline{j}$ .
  
  Dessutom har vi multiplar av dessa tex, $\overline{s} = 3\overline{i} + 12\overline{j}$ .
2. $y = -2x - 1$
  
  Då riktningskoefficenten är -2 rör vi oss 1 steg åt höger och 2 steg nedåt.
  
  En riktningsvektor är $\overline{s} = \overline{i} - 2\overline{j}$ .
  
  En annan är $\overline{s} = -\overline{i} +2\overline{j}$ .
  
  Dessutom har vi multiplar av dessa tex, $\overline{s} = -2\overline{i} +4\overline{j}$ .
3. $y = -\dfrac{1}{4} x -1$
  
  Då riktningskoefficenten är $-\dfrac{1}{4}$ rör vi oss 4 steg åt höger och 1 steg nedåt.
  
  En riktningsvektor är $\overline{s} = 4\overline{i} -\overline{j}$ .
  
  En annan är $\overline{s} = -4\overline{i} +\overline{j}$ .
  
  Dessutom har vi multiplar av dessa tex, $\overline{s} = 8\overline{i} - 2\overline{j}$ .
Bestäm ekvationen för linjen som
1. går genom punkten $(-3,-4)$ och har riktningsvektorn $\overline{s} = \overline{i} + 2\overline{j}$ .
  
  Linjens ekvation är av typ $y-y_0 = k (x-x_0)$ .
  
  Riktningskoefficienten $k = \dfrac{2}{1} = 2$ och punkten är $(-3,-4)$ .
  
  Linjens ekvation är $y-(-4) = 2(x-(-3))$ som är $y = 2x+2$ .
2. går genom punkten $(-2,3)$ och har riktningsvektorn $\overline{s} = 3\overline{i} - 2\overline{j}$ .
  
  Linjens ekvation är av typ $y-y_0 = k (x-x_0)$ .
  
  Riktningskoefficienten $k = \dfrac{-2}{3}$ och punkten är $(-2,3)$ .
  
  Linjens ekvation är $y-3 = -\dfrac{2}{3}(x-(-2))$ som är $y = -\dfrac{2}{3}x+\dfrac{5}{3}$ .
3. går genom punkten $(2,4)$ och har riktningsvektorn $\overline{s} = -\overline{i} - \overline{j}$ .
  
  Linjens ekvation är av typ $y-y_0 = k (x-x_0)$ .
  
  Riktningskoefficienten $k = \dfrac{-1}{-1} = 1$ och punkten är $(2,4)$ .
  
  Linjens ekvation är $y-4 = 1(x-2)$ som är $y = x+2$ .
Är punkten $(0,0,-1)$ på linjen som går genom punkterna $(2,-2,3)$ och $(6,-6,11)$ ?

Om punkterna är på samma linje, kan vi uttrycka $\overrightarrow{AB} = r\overrightarrow{AC}$ där $r \in \mathbf{R}$ .

Vi namnger punkterna, $A = (2,-2,3)$ , $B = (6,-6,11)$ och $C = (0,0,-1)$ .

Vi bildar vektorerna

$\overrightarrow{AB} = 4\overline{i} -4\overline{j} + 8\overline{k}$ .

$\overrightarrow{AC} = -2\overline{i} +2\overline{j} -4\overline{k}$ .

Vi får

$\begin{array}{rcl} \overrightarrow{AB} & = & r\overrightarrow{AC} \\ 4\overline{i} -4\overline{j} + 8\overline{k} & = & r(-2\overline{i} +2\overline{j} -4\overline{k}) \\ 4\overline{i} -4\overline{j} + 8\overline{k} & = & -2r\overline{i} + 2r\overline{j} -4r\overline{k} \\ \end{array}$

Uppdelningen är entydig.

$\left\{ \begin{array}{l} 4 = -2r \\ -4 = 2r \\ 8 = -4r \\ \end{array} \right.$

Eftersom $r = -2$ i alla ekvationer är punkterna på samma linje.
Låt $\overline{a}=-2\overline{i}+4\overline{j}-3\overline{k}$ och $\overline{b}=2\overline{i}+3\overline{j}-5\overline{k}$ . Bilda vektorerna $\overline{a}-\overline{b}$ och $-2\overline{a}+3\overline{b}$ och bestäm längden av dem.

$\overline{a}-\overline{b}=-4\overline{i}+\overline{j}+2\overline{k}$ .

Längden: $\mid\overline{a}+\overline{b}\mid= \sqrt{(-4)^2+1^2+2^2} = \sqrt{21}$ .

$-2\overline{a}+3\overline{b}=10\overline{i}+\overline{j}-9\overline{k}$ .

Längden: $\mid-2\overline{a}+3\overline{b}\mid=\sqrt{10^2+1^2+(-9)^2}=\sqrt{182}$ .
Visa att $\overline{a}=2\overline{i}-3\overline{j}+5\overline{k}$ och $\overline{b}=-6\overline{i}+9\overline{j}-15\overline{k}$ är parallella.

Om två vektorer är parallella skall vi kunna skriva de som $\overline{a} =r\cdot \overline{b}$ där $r \in \mathbf{R}$ .

Om två vektorer är parallella skall vi kunna skriva de som $\overline{a} =r\cdot \overline{b}$ där $r \in \mathbf{R}$ .

Vi tar och gör det.

$\begin{array}{rcl} \overline{a} & = & r\cdot \overline{b} \\ 2\overline{i}-3\overline{j}+5\overline{k} & = & r(-6\overline{i}+9\overline{j}-15\overline{k}) \\ \end{array}$

Väljer vi $r=-\dfrac{1}{3}$ får vi att $2\overline{i}-3\overline{j}+5\overline{k} = -\dfrac{1}{3}(-6\overline{i}+9\overline{j}-15\overline{k})$ .

Eller så jobbar du med entydigheten och bildar ett ekvationssystem.

De är parallella eftersom $\overline{a}=-\dfrac{1}{3}\overline{b}$ .
Är punkten $(0,8,-2)$ på linjen som går genom punkterna $(-1,4,2)$ och $(-3,0,6)$ ?

Om punkterna är på samma linje, kan vi uttrycka $\overrightarrow{AB} = r\overrightarrow{AC}$ där $r \in \mathbf{R}$ .

Vi namnger punkterna, $A = (-1,4,2)$ , $B = (-3,0,6)$ och $C = (0,8,-2)$ .

Vi bildar vektorerna

$\overrightarrow{AB} = -2\overline{i} -4\overline{j} +4\overline{k}$ .

$\overrightarrow{AC} = \overline{i} + 4\overline{j} -4\overline{k}$ .

Vi får

$\begin{array}{rcl} \overrightarrow{AB} & = & r\overrightarrow{AC} \\ -2\overline{i} -4\overline{j} +4\overline{k} & = & r(\overline{i} + 4\overline{j} -4\overline{k}) \\ -2\overline{i} -4\overline{j} +4\overline{k} & = & r\overline{i} + 4r\overline{j} -4r\overline{k} \\ \end{array}$

Uppdelningen är entydig.

$\left\{ \begin{array}{lr} -2 = r & \Leftrightarrow r = -2 \\ -4 = 4r & \Leftrightarrow r = -1 \\ 4 = -4r & \Leftrightarrow r = -1 \\ \end{array} \right.$

Eftersom $r$ inte har samma värde ligger punkterna inte på samma linje.
Bestäm en vektor som är vinkelrät till följande vektorer.
1. $\overline{a} = 5\overline{i} +3\overline{j} -\overline{k}$ och $\overline{b} = 3\overline{j} -2\overline{k}$
  
  Kryssprodukten har värdet $\overline{a} \times \overline{b} = -3\overline{i} +10\overline{j} +15\overline{k}$ . Dessutom har vi multiplar av kryssprodukten.
2. $\overline{c} = -\overline{i}+\overline{j} -\overline{k}$ och $\overline{d} = \overline{i} -2 \overline{j} +\overline{k}$
  
  Kryssprodukten har värdet $\overline{c} \times \overline{d} = -\overline{i} +\overline{k}$ . Dessutom har vi multiplar av kryssprodukten.
3. $\overline{u} = 2\overline{i}-3\overline{k}$ och $\overline{v} = -3\overline{i} +\overline{j}$
  
  Kryssprodukten har värdet $\overline{u} \times \overline{v} = 3\overline{i}+9\overline{i}+2\overline{i}$ . Dessutom har vi multiplar av kryssprodukten.
Bestäm arean av parallellogrammen som bildas av vektorerna $\overline{a} = -3\overline{i} -\overline{j}$ och $\overline{b} = \overline{i} +2\overline{j}$ .

Kryssprodukten $\overline{a} \times \overline{b} = 7\overline{k}$ . Arean för parallellogrammen är 7 a.e.
Bestäm arean av parallellogrammen som bildas av vektorerna $\overline{a} = 2\overline{i} +\overline{j} +\overline{k}$ och $\overline{b} = \overline{i} +2\overline{j} +4\overline{k}$ .

Kryssprodukten $\overline{a} \times \overline{b} = 2\overline{i} -7\overline{j} +3\overline{k}$ .

Arean för parallellogrammen är $\mid \overline{a} \times \overline{b} \mid = \sqrt{(2)^2+(-7)^2+3^2} = \sqrt{62}$ a.e.
Låt f(x,y)=x2+y2−1.
1. Bestäm definitionsmängden
  
  Definitionsmängden är alla reella tal.
2. Bestäm nollställena
  
  Nollstället motsvaras av ekvationen för cirkeln $x^2 + y^2 = 1$ .
3. Bestäm kritiska punkterna
  
  Partialderivatorna är $\partial_x f = 2x$ och $\partial_y f = 2y$ .
  
  Lös ekvationssystemet
  
  $\left\{ \begin{array}{l} 2x = 0 \\ 2y = 0 \\ \end{array} \right.$
  
  och kom fram till punkten $(0,0)$ .
Låt f(x,y)=√−x2+y+4.
1. Bestäm definitionsmängden
  
  Funktionen är definierad då radikanden, det under roten, är positiv. Alltså då $y > x^2 - 4$ .
2. Bestäm nollställena
  
  Nollställena för funktionen är $y = x^2 - 4$
3. Bestäm kritiska punkterna
  
  Partialderivatorna är $\partial_x f = \dfrac{-x}{\sqrt{-x^2+y+4}}$ och $\partial_y f = \dfrac{-\frac{1}{2}}{\sqrt{-x^2+y+4}}$ .
  
  Lös ekvationssystemet
  
  $\left\{ \begin{array}{l} \dfrac{-x}{\sqrt{-x^2+y+4}} = 0 \\ \dfrac{-\frac{1}{2}}{\sqrt{-x^2+y+4}} = 0 \\ \end{array} \right.$
  
  och kom fram till lösningarna att ekvationssystemet saknar lösningar.
  
  Ritar du upp grafen av funktionen märker och inser du att den växer fint av sig och byter aldrig riktning.
Låt f(x,y)=x2−y3−xy.
1. Bestäm definitionsmängden
  
  Definitionsmängden är alla reella tal.
2. Bestäm nollställena
  
  Nollställena kan vi uttrycka med hjälp av $x = \ldots$ . För att göra det utnyttjar vi rotformeln.
  
  Kom fram till $x = \dfrac{y\pm \sqrt{y^2+4y^3}}{2}$ .
3. Bestäm kritiska punkterna
  
  Partialderivatorna är $\partial_x f = 2x-y$ och $\partial_y f = -3y^2-x$ .
  
  Lös ekvationssystemet
  
  $\left\{ \begin{array}{l} 2x-y = 0 \\ -3y^2-x = 0 \\ \end{array} \right.$
  
  och kom fram till lösningarna $(0,0)$ och $(-\dfrac{1}{12},-\dfrac{1}{6})$ .
Låt f(x,y)=x2−sin(y).
1. Bestäm definitionsmängden
  
  Eftersom vi har $x^2$ och $\sin(y)$ vars definitionsmängd är alla reella tal så är $f$ :s definitionsmängd alla reella tal.
2. Bestäm nollställena
  
  Vi får $y = \pm \arcsin(x^2) + 2n\pi$ eller som $y = \pm \sin^{-1}(x^2) + 2n\pi$
3. Bestäm kritiska punkterna
  
  Partialderivatorna är $\partial_x f = 2x$ och $\partial_y f = -\cos(y)$ .
  
  Lös ekvationssystemet
  
  $\left\{ \begin{array}{l} 2x = 0 \\ -\cos(y) = 0 \\ \end{array} \right.$
  
  och kom fram till lösningarna $(0,\dfrac{\pi}{2} + n\pi)$ där $n \in \mathbf{Z}$ .
Bestäm avståndet för punkten $P = (2,7,2)$ från
1. $x$ -axeln.
  
  Situationen är följande
  
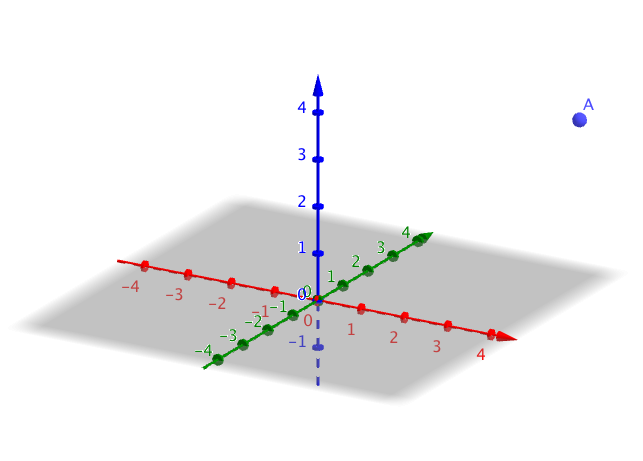
  Avståndet får vi via Pythagoras $d = \sqrt{7^2 + 2^2} = \sqrt{53} \approx 7,3$ l.e.
2. $y$ -axeln
  
  På motsvarande sätt som i a).
  
  Avståndet är $\sqrt{2^2+2^2} = 2\sqrt{2} \approx 2,8$ l.e.
3. $xy$ -planet
  
  Avståndet är samma som $z$ -koordinaten. Alltså 2 l.e.
4. $xz$ -planet.
  
  Avståndet är samma som $y$ -koordinaten. Alltså 7 l.e.
Bestäm volymen som bildas i intervallet $[2,4]$ då $f(x)=\dfrac{1}{x^2}-1$ roterar kring $x$ -axeln.

Vi har $\pi\displaystyle\int_2^4 (\dfrac{1}{x^2}-1)^2 \mathrm{ d} x = \dfrac{295\pi}{192} \approx 4,83$ v.e.
Bestäm volymen som bildas i intervallet $[0,\pi]$ då $f(x)=\sin^2(x)$ roterar kring $x$ -axeln.

Vi har $\pi \displaystyle\int_0^{\pi} (\sin^2(x))^2 \mathrm{ d} x = \dfrac{3}{8}\pi^2 \approx 3,70$ .
För vilka värden på $r$ och $s$ är vektorerna $\overline{a}=\overline{i}-2\overline{j}+6\overline{k}$ och $\overline{b}=r\overline{i}+\overline{j}+s\overline{k}$ parallella. Är de då lika- eller olika riktade?

Då $\overline{a}$ och $\overline{b}$ är parallella gäller att $\overline{a} = t\cdot \overline{b}, t\in \mathbf{R}$ . (Vi använder oss av $t$ eftersom $r$ finns i vektorerna.)

Alltså

$\begin{array}{rcl} \overline{a} & = & t\cdot \overline{b} \\ \overline{i} -2\overline{j}+6\overline{k} & = &t(r\overline{i}+\overline{j}+s\overline{k}) \\ \overline{i} -2\overline{j}+6\overline{k} & = &tr\overline{i}+t\overline{j}+st\overline{k} \\ \end{array}$

Uppdelning i basen är entydig. Alltså gäller att

$\left\{ \begin{array}{rcll} 1 & = & rt \\ -2 & = & t \\ 6 & = & st \\ \end{array} \right.$

Alltså då $t= -2$ är $\overline{a}$ och $\overline{b}$ parallella. Eftersom $t < 0$ är de olika riktade.

Vå får då att $r=-\dfrac{1}{2}$ och $s=-3$ .
Bestäm som parameterframställning ekvationen för linjen som representeras av punkten $( 3,1,-4 )$ och riktningsvektorn $2\overline{i}-7\overline{j}+2\overline{k}$ .

Vi har en punkt $P =(3,1,-4)$ och en riktingsvektor $\overline{s} = 2\overline{i}-7\overline{j}+2\overline{k}$ .

Vi utnyttjar formeln

$\left\{ \begin{array}{l} x = x_0 + ts_x \\ y = y_0 + ts_t \\ z = z_0 + ts_z \\ \end{array} \right.$

Vi får

$\left\{ \begin{array}{rcl} x & = & 3 + 2t \\ y & = & 1 -7t \\ z & = & -4 +2t \quad t \in \mathbb{R}\\ \end{array} \right.$
En triangel bildas av punkterna A=(−2,1,3), B=(2,2,4) och C=(−1,1,−1). Bestäm storleken av vinklarna för triangeln med en tiondels decimals noggrannhet.

Situationen är följande:

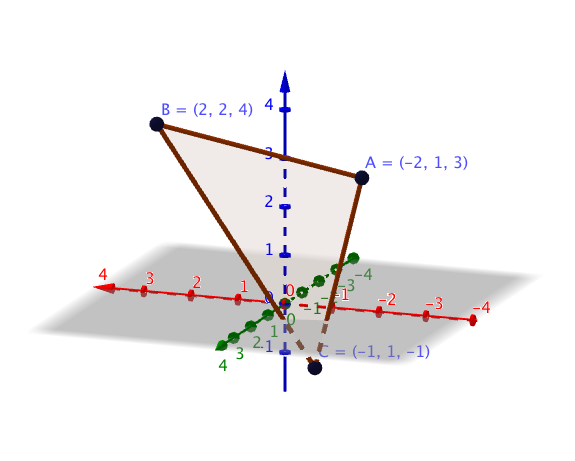
Vi bildar vektorerna.

$\overline{a} = \overrightarrow{AB} = 4\overline{i} + \overline{j} +1\overline{k}$

$\overline{b} = \overrightarrow{AC} = \overline{i} -4\overline{k}$

$\overline{c} = \overrightarrow{BC} = -3\overline{i} -\overline{j} -5\overline{k}$

Längderna av vektorerna är

$\mid \overline{a} \mid = 3\sqrt{2}$

$\mid \overline{b} \mid = \sqrt{17}$

$\mid \overline{c} \mid = \sqrt{35}$

De skalära produkterna är

$\overline{a} \cdot \overline{b} = 0$

$\overline{a} \cdot \overline{c} = -18$

Vi märker att vi borde ha en trubbig vinkel. Det beror på hur vi har definierat vektorerna. Märk att vi måste observera detta då vi bestämmer vinklarna.

$\overline{b} \cdot \overline{c} = 17$

Vi får vinklarna

$\angle(\overline{a},\overline{b}) = 90^{\circ}$

$\angle(\overline{a},\overline{c}) = 135,8^{\circ}$

Vi märker att denna vinkel är för stor då vi jämför med bilden. Det beror på hur vi har definierat vektorerna. Eller så tar vi $\angle(-\overline{a},\overline{c}) = 44,2^{\circ}$

$\angle(\overline{b},\overline{c}) = 45,8^{\circ}$

Eftersom vi får den mindre vinkeln med hjälp av skalära produkten är vinkeln $\angle(\overline{a},\overline{c}) = 180^{\circ} - 135,8^{\circ} = 44,2^{\circ}$ .
1. Bestäm storleken av triangeln med hjälp av vektorer.
  
  Med hjälp av kryssprodukten får vi $A = \dfrac{1}{2} \mid \overline{a} \times \overline{b} \mid = \dfrac{3}{2}\sqrt{34} \approx 8,75$ .
  
  Märk att det är ingen skillnad vilka två vektorer som du utnyttjar.
För vilka värden på k gäller att triangeln som bestäms av punkterna (−3,2), (1,k) och (−1,−4) är rätvinklig.

Vi bildar vektorerna mellan punkterna $A=(-3,2)$ , $B=(1,k)$ och $C=(-1,-4)$ .

$\overrightarrow{AB} = 4\overline{i} + (k-2)\overline{j}$ .

$\overrightarrow{BC} = -2\overline{i} (-4-k)\overline{j}$ .

Eftersom $k$ endast finns i en punkt klarar vi oss med dessa vektorer. Vi bildar den skalära produkten och tvingar att ha värdet 0.

$\begin{array}{rcl} \overrightarrow{AB} \cdot \overrightarrow{BC} & = & 0 \\ 4(-2)+(k-2)\cdot(-4-k) & = & 0 \\ \end{array}$

Ekvationen har lösningarna $k_1 = -2$ och $k_2 = 0$ .
1. Bestäm storleken av bägge trianglar med hjälp av vektorer.
  
  Med hjälp av kryssprodukten får vi $A = \dfrac{1}{2} \mid \overline{a} \times \overline{b} \mid$ .
  
  Då $k_1 = -2$ är arean 8 .
  
  Då $k_1 = 0$ är arean 10 .
Gustave Eiffel planerade det berömda tornet till världsutställningen i Paris 1900. Då tornet blev färdigt var det med sin höjd på 300 m världes högsta byggnad. Tvärsnittsareorna för tornet bildar kvadrater. När man placerar in tornet i ett koordinatsytem följder de kurvan $f(x) = 4,25e^{2,67-0,0089x}$ . Om vi skulle täcka tornet (med skivor, tyg eller dyligt), hur stor blir volymen?

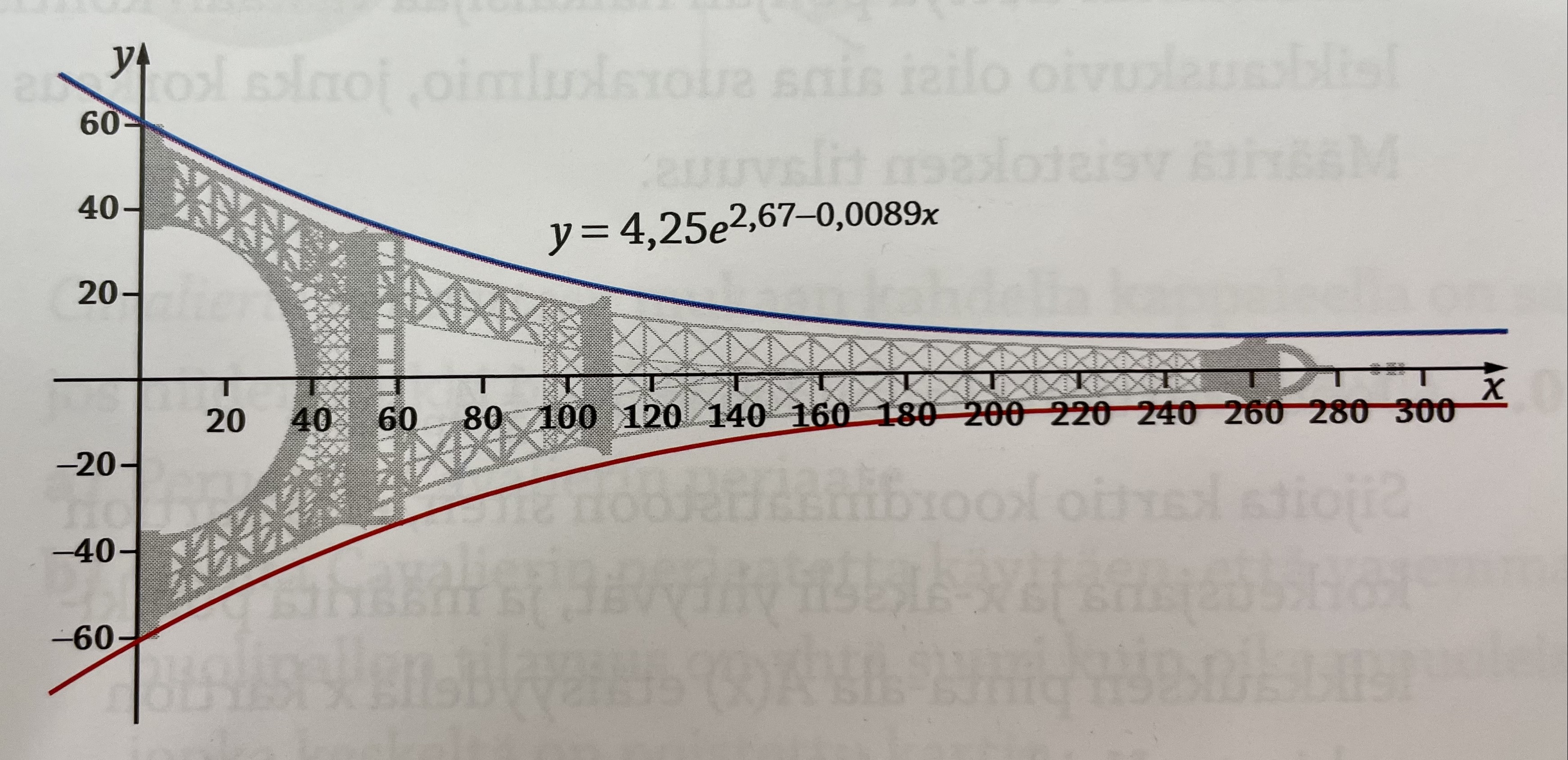
På avståndet $x$ är höjden för tvärsnittsarean $2y = 2\cdot 4,25e^{2,67-0,0089x}$ .

Alltså är tvärsnittsarean $A(x) = (2\cdot 4,25e^{2,67-0,0089x})^2$ .

Integrera från 0 till 300 och kom fram till 840 000 m³.
Bestäm volymen för tältet i figuren. På avståndet $x$ från toppen av tältet bildar tvärsnittsareorna kvadrater med sidan $2\sqrt{x}$ .

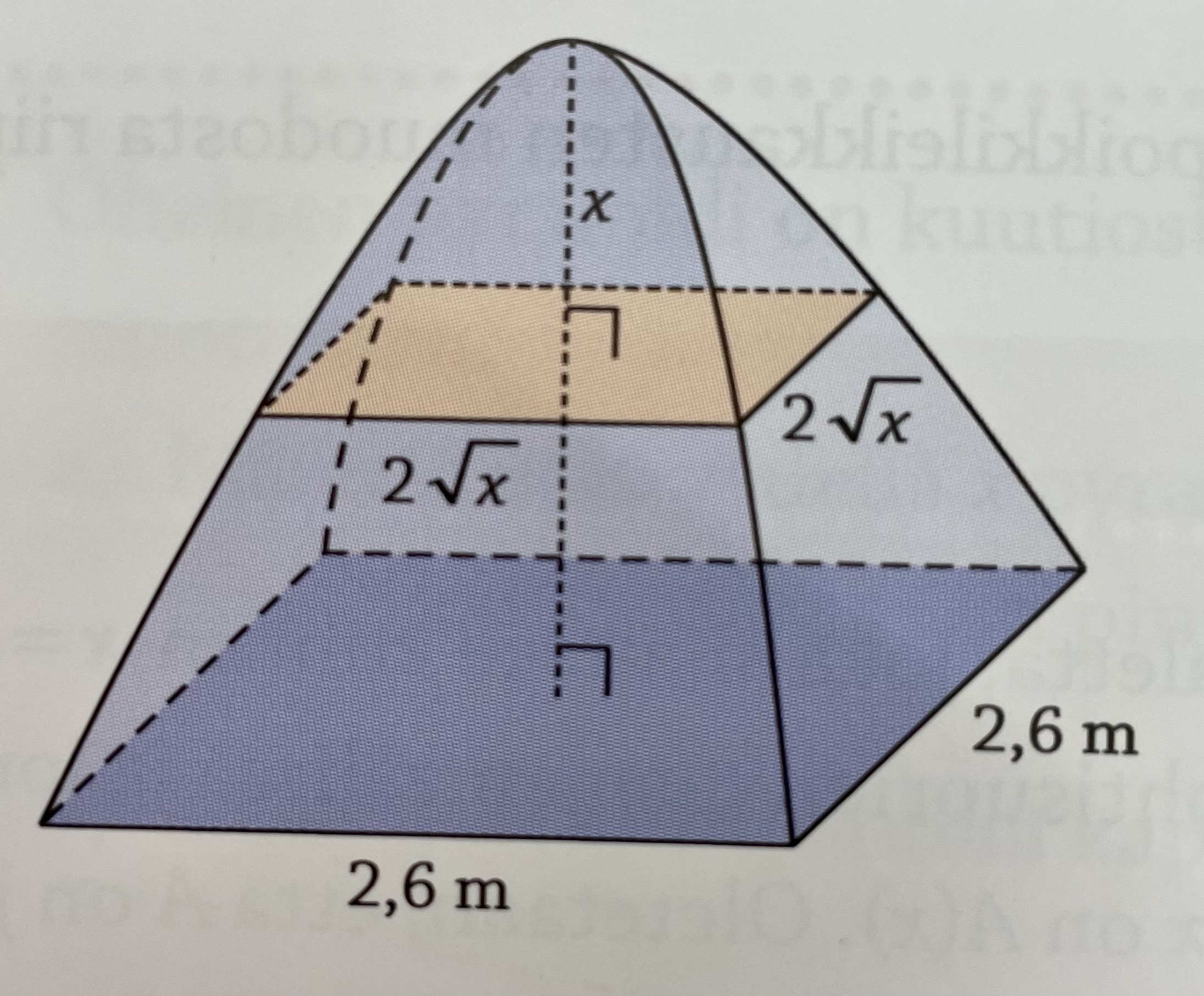
Vi behöver tvärsnittarean $A(x)$ och integreringsgränserna.

På avståndet $x$ från höjden är tvärsnittsarean $A(x)= (2\sqrt{x})^2 = 4x$ .

Höjden för tältet vår vi via bottenarean för tältet.

$2\sqrt{x} = 2,6$ ger oss $x = 1,69$ . Alltså är tältet 1,69 m högt.

Vi får $V = \displaystyle\int_0^{1,69} A(x) \text{ d}x = \displaystyle\int_0^{1,69} 4x \text{ d}x \approx 5,7$ m³.
I vilken punkt skär linjen som går genom $(5,3,8)$ och $(-3,2,3)$ $xy$ -planet?

Bilda en ekvation för linjen. För vilket värde på $z$ skär linjen $xy$ -planet?

Vi behöver en punkt och en riktningsvektor. Beroende på hur vi väljer dem får vi lite olika uträkningar. Däremot är slutsvaret, punkten som vi söker samma.

En riktningsvektor är $\overline{s} = -8\overline{i} -\overline{j}-5\overline{k}$ . En punkt på linjen är $P =(5,3,8)$ .

Linjens ekvation kan se ut som

$\left\{ \begin{array}{rcl} x & = & 5 -8t \\ y & = & 3 -t \\ z & = & 8 -5t \quad t \in \mathbb{R} \\ \end{array} \right.$

Då linjen skär $xy$ -planet är skärningspunkten av typ $Q = (x,y,0)$ . Vi utnyttjar att $z = 0$ för att lösa ut $t$ .

Vi får $t = \dfrac{8}{5}$ .

Vi får de andra koordinaterna genom att sätta in $t =\dfrac{8}{5}$ i linjens ekvation.

Vi får $x = -\dfrac{39}{5}$ och $y = \dfrac{7}{5}$ . Skärningspunkten är $(-\dfrac{39}{5},\dfrac{7}{5},0)$ .
I vilken punkt skär linjen som går genom origo och $(1,-1,2)$ planet som spänns upp av $(-1,3,2)$ , $(2,-5,2)$ och $(3,2,-1)$ .

Vi börjar med att bilda planets ekvation.

$A=(-1,3,2)$ , $B=(2,-5,2)$ och $C=(3,2,-1)$ .

$\overrightarrow{AB} = 3\overline{i} -8\overline{j}$ .

$\overrightarrow{AC} = 4\overline{j}-\overline{j} -3\overline{k}$ .

$\overrightarrow{OA} = -\overline{i} + 3\overline{j} +2\overline{k}$ .

Punkten $P$ har koordinaterna P $(x,y,z)$ .

Vi bildar $\overrightarrow{OP} = \overrightarrow{OA} + r\overrightarrow{AB} + s\overrightarrow{AC}$ .

Vi kommer fram till planets ekvation

$\left\{ \begin{array}{rcl} x & = & -1 +3r -s \\ y & = & 3 -8r +3s \\ z & = & 2 +4s \\ \end{array} \right.$

Eftersom linjen går genom origo och genom punkten är dess riktningsvektor $s = \overline{i} + \overline{j} + \overline{k}$ .

Linjens ekvation är

$\left\{ \begin{array}{rcl} x & = & t \\ y & = & -t \\ z & = & 2t \\ \end{array} \right.$

Vi söker den gemensamma punkten för planet och linjen.

$\left\{ \begin{array}{rcl} t & = & -1 +3r -s \\ -t & = & 3 -8r +3s \\ 2t & = & 2 +4s \\ \end{array} \right.$

Vi får $r = \dfrac{2}{9}$ , $s = -\dfrac{4}{9}$ och $t = \dfrac{1}{9}$ .

Vi sätter in $t = \dfrac{1}{9}$ i linjens ekvation. Vi får skärningspunkten $(\dfrac{1}{9},-\dfrac{1}{9},-\dfrac{2}{9})$ .