3. Skalär produkt i 3 dimensioner

Vi börjar med att studera när vektorerna \(\overline{a}=x_1\overline{i}+y_1\overline{j}+z_1\overline{k}\) och \(\overline{b}=x_2\overline{i}+y_2\overline{j}+z_2\overline{k}\) är vinkelräta. Vi gör det via Pythagoras sats.

Vi placerar \(\overline{a}\) och \(\overline{b}\) så att de börjar i samma punkt.

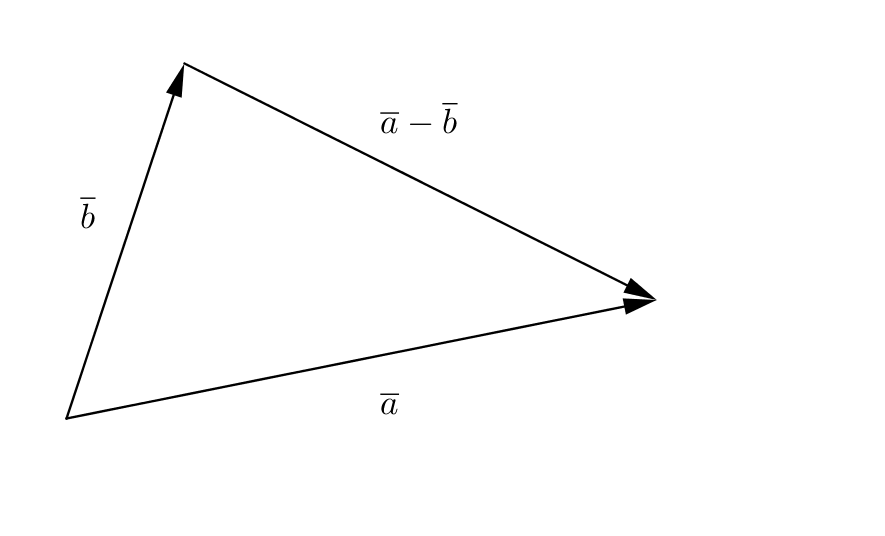
Om triangeln är rätvinklig så gäller att \(\mid \overline{a}-\overline{b} \mid ^2 = \mid \overline{a}\mid ^2 +\mid \overline{b} \mid ^2\).

Vi tar och bildar dessa. \(\mid \overline{a} \mid ^2 = x_1^2 + y_1^2 + z_1^2\) och \(\mid \overline{b} \mid ^2 = x_2^2 + y_2^2 + z_2^2\).

Kvadraten av den tredje längden får vi som

\(\begin{array}{rcl} \mid \overline{a}-\overline{b} \mid ^2\ & = & (x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2 \\ & = & x_1^2-2x_1x_2+x_2^2 + y_1^2-2y_1y_2 + y_2^2 + z_1^2 -2z_1z_2+z_2^2 \\ & = & x_1^2+y_1^2+z_1^2 +x_2^2+y_2^2+z_2^2 -2x_1x_2 -2y_1y_2-2z_1z_2 \\ & = & \mid \overline{a} \mid ^2 + \mid \overline{b} \mid ^2 -2(x_1x_2 + y_1y_2+z_1z_2) \\ \end{array} \)

För att \(\overline{a}\) och \(\overline{b}\) skall vara vinkelräta mot varandra så skall termen \(2(x_1x_2 + y_1y_2+z_1z_2)\) ha värdet noll.

Exempel 1 Är vektorerna \(-\overline{i}+2\overline{j} -2\overline{k}\) och \(4\overline{i}+\overline{j} -\overline{k}\) vinkelräta mot varandra?

Lösning

Jo, eftersom \(-1\cdot 4 + 2\cdot 1 -2(-1)=0\).

Den skalära produkten mellan vektorerna \(\overline{a}=x_1\overline{i}+y_1\overline{j}+z_1\overline{k}\) och \(\overline{b}=x_2\overline{i}+y_2\overline{j}+z_2\overline{k}\) är \(x_1x_2+y_1y_2+z_1z_2\).

Den skalära produkten betecknas \(\overline{a} \cdot \overline{b}\) och utläses "a skalärt b".

Om två vektorer är vinkelräta har den skalära produkten värdet noll.

Exempel 2 Bestäm den skalära produkten för \(\overline{a}=2\overline{i}-\overline{j}\) och \(\overline{b}= -\overline{i}+2\overline{j} -2\overline{k}\).

Lösning

\(\overline{a} \cdot \overline{b}=2(-1) -1\cdot 2 + 0(-2)=-4\).

Exempel 3 Bestäm \(k\) så att \(\overline{a}=3\overline{i}-2\overline{j}\) och \(\overline{b}= k\overline{i}+\overline{j}\) är vinkeräta.

Lösning

Vi får att \(\overline{a}\cdot \overline{b}=0\). Alltså

\(\begin{array}{rcl} 3k-2\cdot1 & = & 0 \\ 3k & = & 2 \\ k & = & \frac{2}{3} \\ \end{array}\)

För den skalära produkten gäller följande egenskaper:

Kommutativ	\(\overline{a} \cdot \overline{b} = \overline{b} \cdot \overline{a}\)
Distributiv	\(\overline{a} \cdot (\overline{b} +\overline{c}) = \overline{a} \cdot \overline{b} +\overline{a} \cdot \overline{c}\)	Om \(\overline{a}\cdot \overline{b}=2\) och \(\overline{a}\cdot \overline{c}=-4\) så är \(\overline{a}(\overline{b}+\overline{c}) = \overline{a}\cdot \overline{b} + \overline{a}\cdot \overline{c} = 2+(-4)=-2\).
Utflyttning av koefficienter	\((s\overline{a}) \cdot \overline{b} = \overline{a} \cdot (s\overline{b}) = s(\overline{a} \cdot \overline{b})\)	Om \(\overline{a} \cdot \overline{b} = 5\) så är \((-4\overline{a}) \cdot \overline{b} = -4(\overline{a} \cdot \overline{b}) = -4 \cdot 5 = -20\) och \(2\overline{a} \cdot (-3\overline{b}) = 2\cdot(-3)(\overline{a} \cdot \overline{b})=-6 \cdot (-5)=30\).
Punktprodukten	\(\overline{a}\cdot \overline{a} = \mid \overline{a} \mid^2\)	Punktprodukten av \(\overline{a}\cdot \overline{a}\) ger längden av \(\overline{a}\) i kvadrat.

Nu tar vi och utgår från vektorer men vi kombinerar dem med cosinussatsen, \(a^2=b^2+c^2-2bc\cos\alpha\), för att komma åt storleken av en vinkel mellan två vektorer då vi utnyttjar den skalära produkten.

Härledning

Vi har \(\overline{a}=x_1\overline{i}+y_1\overline{j}+z_1\overline{k}\) och \(\overline{b}=x_2\overline{i}+y_2\overline{j}+z_2\overline{k}\).

Eftersom vi placerar \(\overline{a}\) och \(\overline{b}\) så att de börjar i samma punkt så är den längre sidan \(\mid \overline{a}-\overline{b}\mid\).

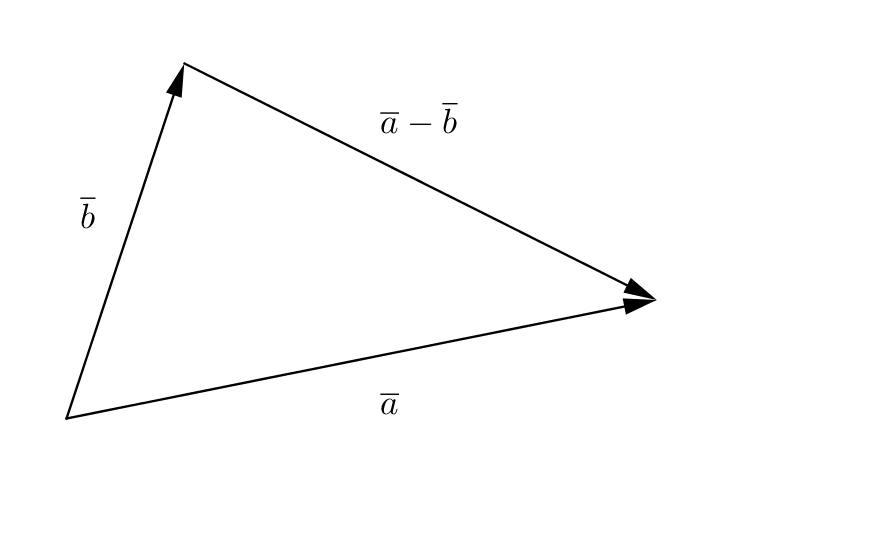
Då vi skriver om cosiunssatsen så att den passar vår triangel får vi att \(\mid \overline{a}-\overline{b}\mid^2=\mid\overline{a}\mid^2+\mid\overline{b}\mid^2-2\mid\overline{a}\mid\mid\overline{b}\mid\cos\alpha\).

Längderna av de kortare sidorna är \(\mid \overline{a} \mid ^2 = x_1^2 + y_1^2 + z_1^2\) och \(\mid \overline{b} \mid ^2 = x_2^2 + y_2^2 + z_2^2\).

Kvadraten av den tredje längden är

\(\begin{array}{rcl} \mid \overline{a}-\overline{b} \mid ^2 & = & (x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2 \\ & = & x_1^2-2x_1x_2+x_2^2 + y_1^2-2y_1y_2 + y_2^2 + z_1^2 -2z_1z_2+z_2^2 \\ & = & x_1^2+y_1^2+z_1^2 +x_2^2+y_2^2+z_2^2 -2x_1x_2 -2y_1y_2-2z_1z_2 \\ & = & \mid \overline{a} \mid ^2 + \mid \overline{b} \mid ^2 -2(x_1x_2 + y_1y_2+z_1z_2).\\ \end{array}\)

När vi jämför hur vi uttryckte cosinussasten med sidorna i vår triangel och hur vi kan uttrycka \(\mid\overline{a}-\overline{b}\mid^2\) så märker vi att vi har nästan samma termer. Det som skiljer är \(x_1x_2+y_1y_2+z_1z_2\) och \(\mid\overline{a}\mid\mid\overline{b}\mid\cos\alpha\). För att vi skall ha identitet så får vi att

\(x_1x_2+y_1y_2+z_1z_2=\overline{a}\cdot \overline{b}=\mid\overline{a}\mid\mid\overline{b}\mid\cos\alpha.\)

Det vi får är skalära produkten för två vektorer.

Skalära produkten mellan \(\overline{a}\) och \(\overline{b}\) får vi som \(\overline{a}\cdot\overline{b} = \mid\overline{a}\mid\mid\overline{b}\mid \cos(\overline{a},\overline{b})\).

Skalära produkten är en operation mellan två vektorer som ger ett värde. Med hjälp av skalära produkten kan vi säga om hur två vektorer förhåller sig till varandra.

Vinkeln mellan två vektorer bestämmer vi som \(\cos(\overline{a}, \overline{b}) = \dfrac{\overline{a}\cdot\overline{b}}{\mid\overline{a}\mid\mid\overline{b}\mid}\).

Vinkeln mellan vektorerna \(\overline{a}\) och \(\overline{b}\) kan vi uppskatta genom att bilda \(\overline{a}\cdot\overline{b}\). Är

\( \overline{a}\cdot\overline{b} < 0 \) är vinkeln trubbig
\( \overline{a}\cdot\overline{b} = 0 \) är vinkeln rät
\( \overline{a}\cdot\overline{b} > 0 \) är vinkeln spetsig.

Exempel 4 Bestäm vinkeln mellan vektorerna \(\overline{a}=\overline{i}-2\overline{j}+\overline{k}\) och \(\overline{b}=2\overline{i}+\overline{j}-2\overline{k}\).

Uppgifter

Bestäm den skalära produkten för
1. \(3\overline{i}+\overline{j}\) och \(\overline{i}+2\overline{j}\).
  
  \( 3 \cdot 1 + 1 \cdot 2 = 5 \)
2. \(3\overline{i}-\overline{j}\) och \(-3\overline{i}+\overline{j}\).
  
  \( 3(-3) + -1\cdot 1 = -10\)
3. \(2\overline{i}\) och \(\overline{i}+2\overline{j}\).
  
  \( 2 \cdot 1 + 0 \cdot 2 = 2\)
Från hörnet i en triangel börjar följande vektorer. Bestäm om triangeln är rätvinklig.
1. \( \overline{a} = 3\overline{i} + 2\overline{j} \) och \( \overline{b} = 2\overline{i} -3 \overline{j} \).
  
  Den skalära produkten mellan \( \overline{a} \cdot \overline{b} = 3\cdot 2 +2(-3) = 0 \). Vinkeln mellan vektorerna är rät.
  
  Triangeln är rätvinklig.
2. \( \overline{a} = 4\overline{i} - 2\overline{j} \) och \( \overline{b} = \overline{i} -8 \overline{j} \).
  
  Den skalära produkten mellan \( \overline{a} \cdot \overline{b} = 4\cdot 1 -2(-8) = 20 \). Vinkeln mellan vektorerna är inte rät.
  
  Den tredje sidan \( \overline{c} = -\overline{a} + \overline{b} = -3\overline{i} -6\overline{j} \) eller \( \overline{a} - \overline{b} \).
  
  \( \overline{a} \cdot \overline{c} = 4(-3) -2(-6) = 0 \). Vinkeln mellan vektorerna är rät.
  
  Triangeln är rätvinklig.
3. \( \overline{a} = 2\overline{i} +2\overline{j} +4\overline{k} \) och \( \overline{b} = -3\overline{i} - \overline{j} +2\overline{k} \).
  
  Den skalära produkten mellan \( \overline{a} \cdot \overline{b} = 2(-3) +2(-1)+4\cdot 2 = 0 \). Vinkeln mellan vektorerna är rät.
  
  Triangeln är rätvinklig.
Är triangeln som består av vektorerna \(\overline{a}=\overline{i}-\overline{j}\), \(\overline{b}=-3\overline{i}-5\overline{j}\) och skillnaden av dessa rätvinklig?

Ja. Vi bestämmer de skalära produkterna. Vi behöver \( \overline{c} = \overline{a}-\overline{b}= 4\overline{i} +4\overline{j}\).

\( \overline{a} \cdot \overline{b} = 1\cdot(-3)+(-1)(-5) = 2\). Dessa är inte vinkelräta.

\( \overline{a} \cdot \overline{c} = 1\cdot 4 +(-1)\cdot 4 = 0\). Dessa är vinkelräta.

\( \overline{b} \cdot \overline{c} = -3\cdot 4 +(-5)\cdot 4 = -32\). Dessa är inte vinkelräta.

Eftersom vi har en triangel så räcker det med att hitta en rät vinkel.
Är triangeln ABC som bestäms av punkterna \((-2,2)\), \((-1,5)\) och \((4,0)\) rätvinklig?

Det räcker att hitta en rät vinkel.

Vi bilar vektorerna mellan punkterna, \(A=(-2,2)\), \(B=(-1,5)\) och \(C=(4,0)\)

\( \overrightarrow{AB} = (-1-(-2))\overline{i} + (5-2)\overline{j} = \overline{i} + 3\overline{j} \).

\( \overrightarrow{AC} = (4-(-2))\overline{i} + (0-2)\overline{j} = 6 \overline{i} - 2\overline{j} \).

\( \overrightarrow{BC} = (4-(-1))\overline{i} + (0-5)\overline{j} = 5 \overline{i} - 5\overline{j} \).

Vi bilar de skalära produkterna.

\( \overrightarrow{AB} \cdot \overrightarrow{AC} = 1\cdot 6 +3(-2) = 0 \). Här är en rät vinkel. (Eftersom vi har hittat den behöver vi inte undersöka de andra.)

\( \overrightarrow{AB} \cdot \overrightarrow{BC} = 1\cdot 5 +3(-5) = -10 \).

\( \overrightarrow{AC} \cdot \overrightarrow{BC} = 6\cdot 5 -2(-5) = 40 \).

Ja, triangeln är rät vinkel vid punkten \( (-2,2) \).
En triangel bildas av punkterna \( A=(0,-1,-2) \), \( B=(1,0,1) \) och \( C =(-2,2,3) \). Bestäm storleken av vinklarna för triangeln med en tiondels decimals noggrannhet.

Situationen är följande:

Från figuren ser vi att vinklarna vid A och C är spetsiga medan B är trubbig.

Vi bildar vektorerna.

\( \overline{a} = \overrightarrow{AB} = (1-0)\overline{i} + (0-(-1))\overline{j} + (1-(-2))\overline{k} = \overline{i} + \overline{j} +3\overline{k} \)

\( \overline{b} = \overrightarrow{AC} = (-2-0)\overline{i} + (2-(-1))\overline{j} + (3-(-2))\overline{k} = -2\overline{i} + 3\overline{j} +5\overline{k} \)

\( \overline{c} = \overrightarrow{BC} = (-2-1)\overline{i} + (2-0)\overline{j} + (3-1)\overline{k} = -3\overline{i} + 2\overline{j} +2\overline{k} \)

Längderna av vektorerna är

\( \mid \overline{a} \mid = \sqrt{11} \)

\( \mid \overline{b} \mid = \sqrt{38} \)

\( \mid \overline{c} \mid = \sqrt{17} \)

De skalära produkterna är

\( \overline{a} \cdot \overline{b} = 16 \)

\( \overline{a} \cdot \overline{c} = 5 \)

\( \overline{b} \cdot \overline{c} = 22 \)

Vi får vinklarna

\( \angle(\overline{a},\overline{b}) = 38,5^{\circ} \)

\( \angle(\overline{a},\overline{c}) = 68,6^{\circ} \)

\( \angle(\overline{b},\overline{c}) = 30,1^{\circ} \)

Eftersom vi får den mindre vinkeln med hjälp av skalära produkten är vinkeln \( \angle(\overline{a},\overline{c}) = 180^{\circ} - 68,6^{\circ} = 111,4^{\circ} \).

Triangelns vinkelsumma är 38,5^o+111,4^o+30,1^o = 180^o.
För vilka värden på \(k\) gäller att triangeln som bestäms av punkterna \((-4,1)\), \((k,4)\) och \((-3,6)\) är rätvinklig.

Vi bildar vektorerna mellan punkterna \(A=(-4,1)\), \(B=(k,4)\) och \(C=(-3,6)\).

\( \overrightarrow{AB} = (k-(-4))\overline{i} + (4-1)\overline{j} = (k+4)\overline{i} + 3\overline{j} \).

\( \overrightarrow{BC} = (-3-k)\overline{i} + (6-4)\overline{j} = (-3-k)\overline{i} +2\overline{j} \).

Eftersom \( k \) endast finns i en punkt klarar vi oss med dessa vektorer. Vi bildar den skalära produkten och tvingar att ha värdet 0.

\( \begin{array}{rcl} \overrightarrow{AB} \cdot \overrightarrow{BC} & = & 0 \\ (k+4)(-3-k)+3\cdot 2 & = & 0 \\ \end{array} \)

Ekvationen har lösningarna \( k_1 = -6 \) och \( k_2 = -1 \).
Bestäm för linjen \(2x-6y-6=0\)
1. en riktningsvektor
  
  \( 2x-6y -6 = 0 \Leftrightarrow y = \dfrac{1}{3}x +1 \).
  
  Riktningsvektorerna är \(3\overline{i}+\overline{j}\) eller \(-3\overline{i}-\overline{j}\) och multiplar av dessa.
2. en normalvektor (en vektor som bildar en normal)
  
  Eftersom linjens riktningskoefficient är \( \dfrac{1}{3} \) så är normalens riktningskoefficient \( -3 \). (Produkten skall ha värdet \( -1 \).)
  
  Riktningsvektorerna är \(-\overline{i}+3\overline{j}\) eller \(\overline{i}-3\overline{j}\) och multiplar av dessa.
3. en normalvektor vars längd är 1
  
  Vi söker enhetsvektorn för normalvektorn, \( \overline{n}^0 = \dfrac{1}{\mid \overline{n} \mid }\cdot \overline{n} \).
  
  Längden av vektorn \( -\overline{i}+3\overline{j} \) är \( \sqrt{(-1)^2+3^2} = \sqrt{10} \).
  
  Normalvektorns enhetsvektor är \(\dfrac{1}{\sqrt{10}}(-\overline{i}+3\overline{j})\) eller \(\dfrac{1}{\sqrt{10}}(\overline{i}-3\overline{j})\).
4. en normalvektor vars längd är 10.
  
  Längden av de vektorer som vi bestämde i c) har längden 1. Vi gör dem 10 ggr längre.
  
  Vi får \(\dfrac{10}{\sqrt{10}}(-\overline{i}+3\overline{j}) = \sqrt{10}(-\overline{i}+3\overline{j})\) eller \(\sqrt{10}(\overline{i}-3\overline{j})\).
Om vektorn \( \overline{a} \) som finns i \( xy \)-planet vet vi att \( \overline{a} \cdot \overline {i} = 3 \) och att \( \overline{a} \cdot \overline {j} = 6 \). Bestäm vektorn \( \overline{a} \).

Vi betecknar \( \overline{a} = x\overline{i} + y\overline{j} \). De skalära produkterna ger oss ekvationerna \( x\cdot 1 + y\cdot 0 = 3 \) och \( x\cdot 0 + y\cdot 1 = 6 \) ger oss lösningarna.

Alltså \( \overline{a} = 3\overline{i} + 6\overline{j} \).
Hitta i alla fall fyra vektorer som alla har olika längd som är vinkelräta mot \(\overline{a}=\overline{i}+2\overline{j}+\overline{k}\).

Vektorerna är av typ \( \overline{b} = x\overline{i} + y\overline{j} + z\overline{k} \).

Då \( \overline{a} \) och \( \overline{b} \) skall vara vinkelräta skall den skalära produkten ha värdet 0.

Vi får \( 1\cdot x +2\cdot y +1\cdot z =0 \).

Testa dig fram (;

Tex: \(-\overline{j}+2\overline{k}\), \(\overline{i}-\overline{k}\), \(-4\overline{i}+2\overline{j}\) och \(-4\overline{i}+\overline{j}+2\overline{k}\).
Låt \( \overline{a} = \overline{i} + 2\overline{j} + \overline{k} \) och \( \overline{b} = s\overline{i} + \overline{j} - \overline{k} \). Bestäm \( s \) så att vektorerna \( \overline{a} + \overline{b} \) och \( \overline{a} - \overline{b} \) är vinkelräta mot varandra.

Bilda vektorerna \( \overline{a} + \overline{b} = (1+s)\overline{i} + 3\overline{j} \) och \( \overline{a} - \overline{b} = (1-s)\overline{i} + \overline{j} +2\overline{k}\).

Bilda skalära produkten av dessa och låt den få värdet 0.

Kom fram till \( s = 2 \) eller \( s = -2 \).
I triangeln \( ABC \) gäller att \( \overline{AB} = 3\overline{i} + \overline{j} - \overline{k} \) och \( \overline{AC} = \overline{i} - \overline{j} + \overline{k} \). Bestäm storleken av vinklarna i triangeln med en grads noggrannhet.

Vi får \( \measuredangle A \approx 80^{\circ}, \measuredangle B \approx 29^{\circ} \) och \( \measuredangle C \approx 71^{\circ} \).
För vilka punkter på \( z \)-axeln gäller att sträckan mellan \( A=(4,1,2) \) och \( B=(-5,6,-3) \) syns ur en rät vinkel?

Punkterna på \( z \)-axeln är av formen \( P=(0,0,z) \).

Bilda vektorerna \( \overline{PA} \) och \( \overline{PB} \). Utnyttja sedan att skalära produkten skall ha värdet 0.

Punkterna är \( (0,0,4) \) och \( (0,0,-5) \).
En linje går genom punkterna \( (-1,0,3) \) och \( (1,3,2) \). Bestäm storleken av vinkeln som linjen bildar med följande plan.
1. \( xy \)-planet.
  
  Riktningsvektorn för linjen är \( \overline{s} = (-1-1)\overline{i} + (0-3)\overline{j} + (3-2)\overline{k} = -2\overline{i} -3\overline{j} + \overline{k} \).
  
  Eller så kommer du till \( \overline{s} = 2\overline{i} +3\overline{j} - \overline{k} \).
  
  Den vektor som är i \( xy \)-planet och har samma riktning är \( \overline{a} = -2\overline{i} -3\overline{j} \).
  
  Vi bestämmer vinkeln mellan dessa.
  
  \( \overline{a} \cdot \overline{s} = -2(-2) -3(-3) + 0\cdot 1 = 13 \).
  
  \( \mid \overline{a} \mid = \sqrt{2^2+(-3)^2} = \sqrt{13} \).
  
  \( \mid \overline{s} \mid = \sqrt{(-2)^2+(-3)^2+1^2} = \sqrt{14} \).
  
  \( \cos (\overline{a},\overline{s}) = \dfrac{13}{\sqrt{13}\cdot\sqrt{14}} \)
  
  Vinkeln är \( 15,5^{\circ}\).
2. \( yz \)-planet.
  
  Den vektor som är i \( yz \)-planet och har samma riktning är \( \overline{a} = -3\overline{j} +\overline{k} \).
  
  Vi bestämmer vinkeln mellan dessa.
  
  \( \overline{a} \cdot \overline{s} = -2\cdot 0 -3(-3) + 1\cdot 1 = 10 \).
  
  \( \mid \overline{a} \mid = \sqrt{(-3)^2+1^2} = \sqrt{10} \).
  
  \( \mid \overline{s} \mid = \sqrt{(-2)^2+(-3)^2+1^2} = \sqrt{14} \).
  
  \( \cos (\overline{a},\overline{s}) = \dfrac{10}{\sqrt{10}\cdot\sqrt{14}} \)
  
  Vinkeln är \( 32,3^{\circ}\).
Ett flygplan startar från punkten \((2,4,0)\) och lyfter i riktningen \( 2\overline{i}+3\overline{j}+\overline{k} \). Hur stor vinkel bildar flygplanets rutt mot marken? Svara med noggrannheten 0,1 grader.

Rita bild och fundera. Hur kan du uttrycka den vektor som går längs med marken och beskriver planets rutt?

Vektorn som beskrivers flygplanets rutt längd med marken är \( \overline{s} = 2\overline{i}+3\overline{j} \).

Vektorn som beskriver flygplanets rutt är \( \overline{a}= 2\overline{i}+3\overline{j}+\overline{k} \).

Vi bestämmer vinkeln mellan dessa.

\( \overline{a} \cdot \overline{s} = 2\cdot 2 +3\cdot 3 + 1\cdot 0 = 13 \).

\( \mid \overline{a} \mid = \sqrt{2^2+3^2+1^2} = \sqrt{14} \).

\( \mid \overline{s} \mid = \sqrt{2^2+3^2} = \sqrt{13} \).

\( \cos (\overline{a},\overline{s}) = \dfrac{13}{\sqrt{14}\cdot\sqrt{13}} \)

Vinkeln är \( 15,5^{\circ}\).
I triangeln \( ABC \) gäller att \( \overline{AB} \cdot \overline{CB} = \overline{BA} \cdot \overline{CA} \). Visa att sidorna \( BC \) och \( AC \) är lika långa.

Till exempel på följande sätt.

Vi betecknar \( \overrightarrow{AB} = \overline{a} \) och \( \overrightarrow{AC} = \overline{b} \), då är \( \overrightarrow{CB} = \overline{a}-\overline{b} \).

\( \overline{AB} \cdot \overline{CB} = \overline{a} \cdot (\overline{a}-\overline{b}) \).

\( \overline{BA} \cdot \overline{CA} = -\overline{a} \cdot -\overline{b} \).

\( \overline{AB} \cdot \overline{CB} = \overline{BA} \cdot \overline{CA} \) är samma som \( \overline{AB} \cdot \overline{CB} - \overline{BA} \cdot \overline{CA} = 0 \), alltså \( \overline{a} \cdot (\overline{a}-\overline{b}) - (-\overline{a} \cdot -\overline{b}) = 0 \).

Alltså

\( \begin{array}{rcll} \mid \overline{a} \mid^2 -2(\overline{a} \cdot \overline{b}) & = & 0 & \mid + \mid \overline{b}\mid^2 \\ \mid \overline{a} \mid^2 -2(\overline{a} \cdot \overline{b}) +\mid \overline{b}\mid^2 & = & \mid \overline{b}\mid^2 \\ (\overline{a}-\overline{b})^2 & = & (\overline{b})^2 \\ \overline{a}-\overline{b} & = & \overline{b} \\ \end{array} \)

Alltså är \( BC \) lika lång som \( AC \).