8. Additionsprincipen
Anna, Bertil, Cecilia och Daniel har gjort följande tabell över sina egenskaper:
| Kön | höger/vänsterhänt | ögonfärg | |
|---|---|---|---|
| Anna | flicka | högerhänt | blåa ögon |
| Bertil | pojke | högerhänt | bruna ögon |
| Cecilia | flicka | vänsterhänt | blåa ögon |
| Daniel | pojke | högerhänt | blåa ögon |
De funderar på följande:
Vilken är sannolikheten att av dem väljs slumpmässigt en flicka eller en vänsterhänt person.
Sannolikheten för en flicka är \( \dfrac{2}{4} \) och sannolikheten för att personen är vänsterhänt är \( \dfrac{1}{4} \). Det som vi måste beakta är att vi har en flicka som är vänsterhänt, sannolikheten att hon blir vald är \( \dfrac{1}{4} \).
Vår sökta sannolikhet är \( \dfrac{2}{4}+\dfrac{1}{4}-\dfrac{1}{4} = \dfrac{1}{2} \).
Allmänt har vi händelserna A och B. Då vi söker sannolikheten för A eller B måste vi beakta den sannolikhet då A och B gäller samtidigt.
Sannolikheten för P(A eller B) = P(A) - P(B) - P(A och B).
Grafiskt ser vi det som följande:
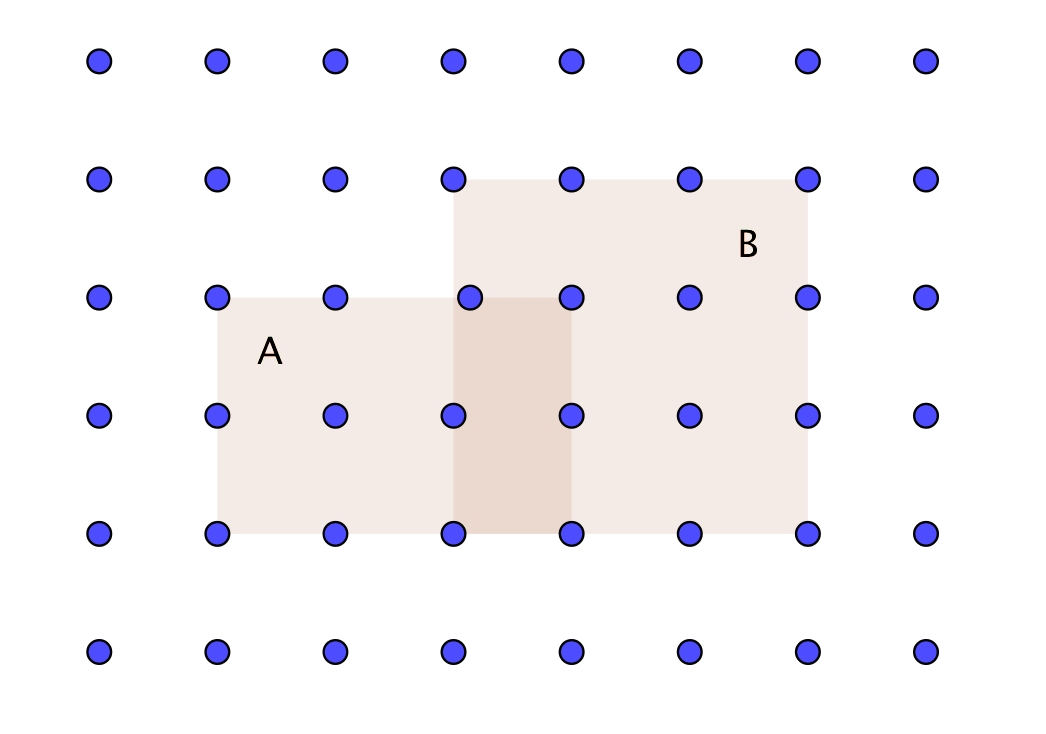
Vi har de olika sannolikheterna, sedan måste vi ta bort den gemensamma delen.
Exempel 1 Ur en kortpacke dras två kort. Bestäm sannolikheten att bägge kort är röda (hjärter eller ruter) eller att bägge kort är åttor.
Lösning
För varje färg finns det kort med valören åtta. Dessa kort måste vi beakta då vi bestämmer sannolikheten.
Sannolikheten är P(båda röda) + P(båda åttor) - P(båda röda och valören åtta).
I packen finns det 26 st röda kort och 4 st åttor.
Sannolikheten är \( P(\text{båda röda eller åttor}) = \dfrac{26\cdot 25}{52\cdot 51} + \dfrac{4\cdot 3}{52\cdot 51} - \dfrac{2\cdot 1}{52\cdot 51} = 0,248868\ldots \approx 0,249 \).
Exempel 2 Rhesus egenskapen är beroende av folkgrupper. Av den baskiska befolkningen är 65 % Rhesus positiva, Rh+. Bestäm sannolikheten att i en baskisk familj där båda föräldrar är basker
- är båda föräldrar Rhesus negativa
- har båda föräldrar samma Rhesusegenskap
Lösning
- Andelen Rhesusnegativa, utan Rhesus faktorn, är 1 - 0,65 = 0,35. Sannolikheten att båda föräldar är Rhesusnegativa är \( P(Rh-) \cdot P(Rh-) = 0,35 \cdot 0,35 = 0,1225 \approx 0,123 \).
- Då båda föräldrar skall ha samma Rhesus egenskap gäller att bägge föräldrar är Rh+ eller Rh-. Eftersom Rhesusegenskapen utesluter varandra, antingen har du den eller inte, så behöver vi inte beakta något annat.
Sannolikheten är \( P(\text{Båda Rh+}) + P(\text{Båda Rh-}) - P(\text{Olika Rh}) = 0,65 \cdot 0,65 + 0,35 \cdot 0,35 = 0,545 \).
Om två händelser A och B utesluter varandra, som i exemplet ovan gäller att P(A eller B) = P(A) + P(B).
Uppgifter
- Vilken är sannolikheten att vi ur en kortpacke drar en tvåa eller en fyra? Vi räknar med att ässet har valören 1.
Vi får \( P(\text{2 eller 4:a}) = \dfrac{4}{52}+\dfrac{4}{52} = 0,15385 \).
- Ur en kortpacke drar vi två kort. Bestäm sannolikheten att bägge kort är spader eller bildkort? Som bildkort räknas knekt, dam, kung och ess.
Sannolikheten att bägge kort är spader är \( P(\text{bägge spader}) = \dfrac{13}{52} \cdot \dfrac{12}{51} \).
Att bägge kort är bildkort är \( P(\text{bildkort}) = \dfrac{16}{52} \cdot \dfrac{15}{51} \).
Spader bildkort är \( P(\text{spader och bildkort}) = \dfrac{4}{52} \cdot \dfrac{3}{51} \).
Sannolikheten är \( \dfrac{13}{52} \cdot \dfrac{12}{51} + \dfrac{16}{52} \cdot \dfrac{15}{51} - \dfrac{4}{52} \cdot \dfrac{3}{51} = 0,1447\ldots \).
Alltså 0,14.
- Utesluter följande händelser varandra?
Påstående Utesluter varandra Utesluter inte varandra Vi kastar en tärning två gånger. A: första kastet ger en fyra.
B: andra kastet ger en trea.
Vi kastar en tärning två gånger. A: första kastet är udda.
B: första kastet är jämt.
Vi kastar en tärning två gånger. A: första kastet ger en fyra och andra kastet ger en sexa.
B: första kastet ger en fyra och andra kastet ger en fyra.
A: Anna försenar sig från skolan.
B: Börje försenar sig från skolan.
Vi planterar tulpaner och solrosor. Exakt en blomma gror. Påstående Utesluter varandra Utesluter inte varandra Vi kastar en tärning två gånger. A: första kastet ger en fyra.
B: andra kastet ger en trea.
Vi kastar en tärning två gånger. A: första kastet är udda.
B: första kastet är jämt.
Vi kastar en tärning två gånger. A: första kastet ger en fyra och andra kastet ger en sexa.
B: första kastet ger en fyra och andra kastet ger en fyra.
A: Anna försenar sig från skolan.
B: Börje försenar sig från skolan.
Vi planterar tulpaner och solrosor. Exakt en blomma gror. - Vilken är sannolikheten att vi ur en kortpacke drar ett kort som är spader eller att valören är mindre än 7? Vi räknar med att ässet har valören 1.
Vi får sannolikheten \( P(\text{spader eller valören mindre än 7})= P(\text{Spader}) + P(\text{Mindre än 7}) -P(\text{Spader vars valör är mindre än 7}) = \)
\( \dfrac{13}{52} + \dfrac{4\cdot 6}{52} -\dfrac{6}{52}= \dfrac{31}{52} = 0,59615\ldots \approx 0,596 \).
- I låda 1 finns det ett vit och två svarta klot. I låda 2 finns det 2 vita och 3 svarta klot. Vi väljer slumpmässigt en låda och från lådan drar vi ett slumpmässigt klot. Bestämm sannolikheten att klotet som vi drar är vitt.
För att dra ett vitt klot skall vi först välja låda 1 och sedan dra ett vitt klot, eller välja låda 2 och därifrån dra ett vitt klot.
Vi får sannolikheten \( P(\text{låda 1 och vitt klot}) + P(\text{låda 2 och vitt klot}) \\ = P(\text{låda 1})\cdot P(\text{vit klot}) + P(\text{låda 2})\cdot P(\text{vit klot}) \\ = \dfrac{1}{2} \cdot \dfrac{1}{3} + \dfrac{1}{2}\cdot\dfrac{2}{5} = \dfrac{11}{30} = 0,366\ldots \).
Alltså 0,37.
- Vi kastar en tärning 4 gånger. Bestäm sannolikheten att vi får exakt en 6:a.
6:an kan komma på första, andra, tredje eller fjärde kastet. Sannolikheterna för kasten är oberoende av varandra.
Vi får sannolikheten \( P(\text{4 kast, en 6:a}) = \\ = \dfrac{1}{6} \cdot \dfrac{5}{6} \cdot \dfrac{5}{6} \cdot \dfrac{5}{6} + \dfrac{5}{6} \cdot \dfrac{1}{6} \cdot \dfrac{5}{6} \cdot \dfrac{5}{6} \\ + \dfrac{5}{6} \cdot \dfrac{5}{6} \cdot \dfrac{1}{6} \cdot \dfrac{5}{6} + \dfrac{5}{6} \cdot \dfrac{5}{6} \cdot \dfrac{5}{6} \cdot \dfrac{1}{6} = 4 \cdot \dfrac{1}{6} \cdot (\dfrac{5}{6})^3 = 0,3858\ldots \)
Alltså 0,39.
- Två reella tal, \( x \) och \( y \) väljs slumpmässigt ur intervallet \( [-1,4] \). Bestäm sannolikheten att
- \( x > 3 \) eller \( y < 0 \).
\( P(x > 3 \text{ eller } y < 0) = P(x > 3)+P(y < 0)= \dfrac{1}{5} + \dfrac{1}{5} = \dfrac{2}{5} = 0,40 \).
- \( y < x-1 \) eller \( x < y-1 \).
Vi får \( P(y < x-1 \text{ eller } x < y-1) = P(y < x-1) + P(x < y-1) = \dfrac{\dfrac{1}{2}\cdot 4 \cdot 4}{5\cdot 5} + \dfrac{\dfrac{1}{2}\cdot 4 \cdot 4}{5\cdot 5}=\dfrac{16}{25} = 0,64 \).
- \( x > 3 \) eller \( y < 0 \).
- I en finalmatchserie möts HC Hakkila och Martsarin Myrsky Hockey. För att vinna mästerskapet krävs 4 segrar. Under säsongens tidigare matcher har HC Hakkila vunnit 4 matcher av 6 som lagen möts i. Bestäm sannolikhten att matchserien är över efter 4 st matcher.
För att matchserien skall vara över efter 4 st matcher så skall något dera lag vinna 4 matcher på raken.
Vi får sannolikheten \( P(\text{HC Hakkila vinner 4 eller Martsarin Myrsky Hockey vinner 4}) = \\ P(\text{HC Hakkila vinner 4}) + P(\text{Martsarin Myrsky Hockey vinner 4}) = \\ \dfrac{4}{6}\cdot\dfrac{4}{6}\cdot\dfrac{4}{6}\cdot\dfrac{4}{6} + \dfrac{2}{6}\cdot\dfrac{2}{6}\cdot\dfrac{2}{6}\cdot\dfrac{2}{6} = \\ (\dfrac{4}{6})^4 + (\dfrac{2}{6})^4 = 0,20987\ldots \)
Alltså 0,21.
- Bestäm sannolikheten att Martsarin Myrsky Hockey vinner mästerskapet efter 5 st matcher.
För att Martsarin Myrsky Hockey skall vinna får HC Hakkila vinna den första, andra eller tredje matchen.
Vi får sannolikheten \( P(\text{Martsarin Myrsky Hockey vinner efter 5 matcher}) = \\ \dfrac{4}{6}\cdot\dfrac{2}{6}\cdot\dfrac{2}{6}\cdot\dfrac{2}{6} + \dfrac{2}{6}\cdot\dfrac{4}{6}\cdot\dfrac{2}{6}\cdot\dfrac{2}{6} + \dfrac{2}{6}\cdot\dfrac{2}{6}\cdot\dfrac{4}{6}\cdot\dfrac{2}{6} = \\ 3\cdot \dfrac{4}{6}\cdot(\dfrac{2}{6})^3 = 0,0740\ldots \)
Alltså 0,07.
- Bestäm sannolikheten att HC Hakkila vinner mästerskapet efter den 7 matchen.
För att gå till en 7:e match krävs att båda lagen vinner 3 st matcher av 6 st.
Antal kombinationer för det är \( \displaystyle {6 \choose 3} \).
Sedan behöver HC Hakkila vinna den sista.
Vi får sannolikheten \( P(\text{HC Hakkila vinner 7 matchen}) = \displaystyle {6 \choose 3} \cdot (\dfrac{4}{6})^3 (\dfrac{2}{6})^3 \cdot \dfrac{4}{6} = 0,1463\ldots \)
Alltså 0,15.
- Bestäm sannolikheten att Martsarin Myrsky Hockey vinner mästerskapet efter 5 st matcher.