15. Korrelation
I arbetet om kurskamraternas längder som Anna, Bertil, Cecilia och Daniel fick de som respons att undersöka om det finns ett samband mellan hur könet påverkar längden. Inom statistik talar vi om att undersöka om det finns en korrelation, samband, mellan två variabler.
Vi undersöker om könet korrelerar med längden.
Men före vi gör det studerar vi följande tre bilder.
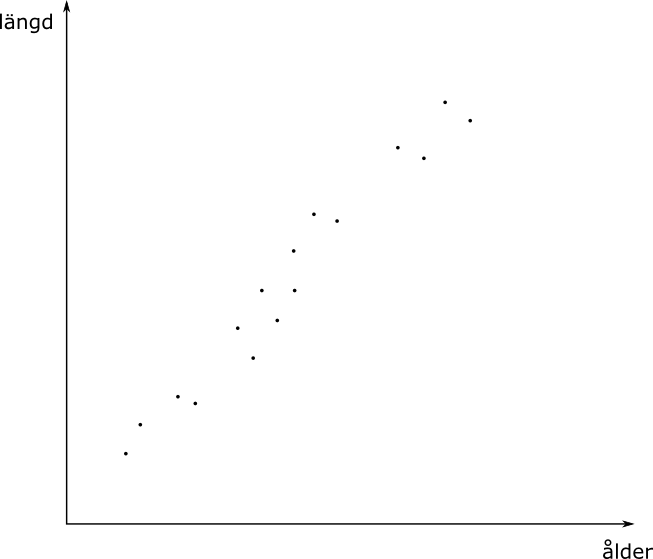
Bild 1, Samband mellan längd och ålder?
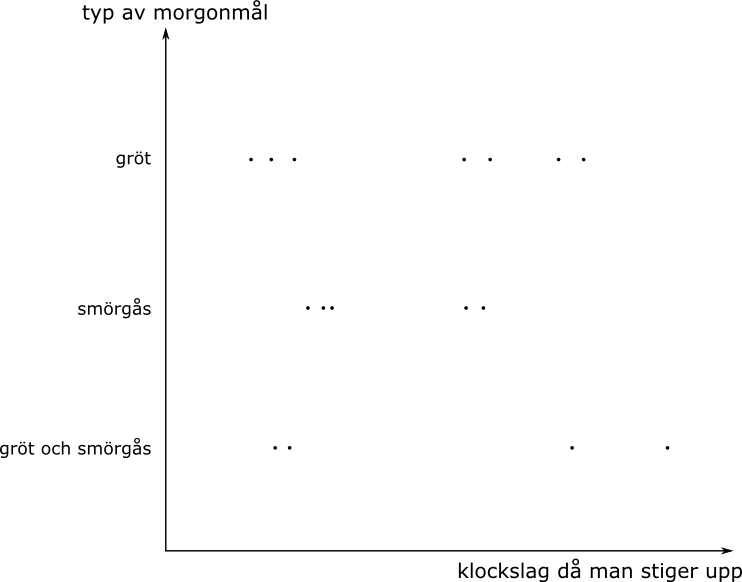
Bild 2, Samband mellan typ av morgonmål och när man stiger upp?
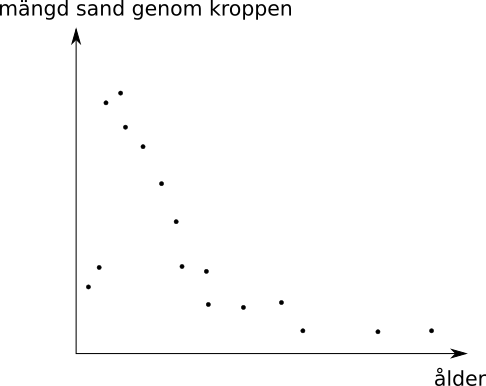
Bild 2, Samband mellan mängd av sand genom kroppen och ålder?
I bild 1 har vi punkterna fint samlade. Du märker att de nästan lägger sig på en linje. Här har vi ett bra samband mellan ålder och längd. Vi har en positiv korrelation.
I bild 2 märker vi igen att punkterna är spridda över hela grafen. Här finns ingen direkt korrelation mellan när du stiger upp på morgonen och vad du äter till morgonmål. Korrelationen är nära noll.
Bild 3 påminner om bild 1 på så sätt att punkterna är fint samlade. Vi har ett samband mellan ålder och hur mycket sand som far genom kroppen, där mängden sand minska med åldern. Vi har en negativ korrelation.
För att mäta hur bra två variabler korrelerar använder vi oss av Pearsons och Spearmans korrelationskoefficienter. Det viktiga som du skall veta är att värdet för korrelationen, r, ligger mellan -1 och 1. Då \( \mid r \mid > 0,8 \) har vi en stark korrelation.
| Värdet på \( r \) | Korrelation |
|---|---|
| 0 - 0,30 | betydelselös |
| 0,30 - 0,60 | måttlig |
| 0,60 - 0,80 | märkbar |
| 0,80 - 1 | stark |
Nu är vi färdiga att gå tillbaka till könen och längden. Eftersom vi inte kan pricka in flicka och pojke ger vi dem värdena 1 och 2 (eller 2 och 3. Det är ingen skillnad så länge de har något värde).
Tabellen blir och se ut som följande:
| Kön ( 1 = flicka, 2 = pojke) | Längd (cm) |
|---|---|
| 1 | 156 |
| 1 | 159 |
| 1 | 163 |
| 1 | 164 |
| 1 | 168 |
| 1 | 174 |
| 2 | 163 |
| 2 | 175 |
| 2 | 178 |
| 2 | 179 |
| 2 | 181 |
| 2 | 187 |
Hur vi bestämmer korrelationen med LibreOffice framgår i videon.
På LibreOfficeCalc får du fram korrelationskoefficienten antingen via en graf eller så direkt med kommandot =korrel().
Uppgifter
- Daniel som jobbar deltid i sin pappas paraplyaffär gjorde upp följande statistik under en period en höst. Undersök utgående från datan i tabellen nedan om det finns en korrelation mellan regnmängden och antalet sålda paraplyer.
Total regnmängd för dagen (mm) Antal sålda paraplyn 3,4 13 2,1 15 0 3 0 0 0 1 5,6 17 1,2 7 0 2 0 0 4,5 8 1,2 4 0 0 - Bestäm värdet på \( R^2 \).
0,73
- Korrelationen är
Stark
- Bestäm värdet på \( R^2 \).
- En lärare gjorde följande observationer över sina elever sina abiturienter som studerade och skrev långa matematiken.
Medeltal av MaA kurser Vitsord i studentexamen 9,8 e 9,5 l 8,9 l 8,5 m 8,4 m 8,3 m 7,9 m 7,3 c 7,2 m 6,9 c 6,5 b 6,2 a 5,8 b 5,7 a Korrelerar vitsordet i studentexamen med medeltalet för kurserna? Vitsordsskalan i studentexamen går från l, som högst till, e, m, c, b, a och i som underkänt.
- \( R^2 \) har värdet
0,85
- Korrelationen är
Stark
- Finns det ett samband mellan kursvitsorden och vitsordet i studentskrivningarna?
Ja!
- \( R^2 \) har värdet
- Anna och Bertil gjorde ett statistiskt arbete över om det finns en korrelation mellan längden av skolvägen och tiden som man kommer i tid till första lektionen. De följde med sina klasskamraters tider under en vecka och de fick följande data.
Avstånd till skolan (km) Minuter man är på plats före lektionen börjar. + är i tid, - är försenad. 1,5 5 1,7 5 1,8 5 2,0 5 3,6 5 0,4 -2 1,2 7 0,8 -4 5,3 10 0,1 1 1,3 -3 1,7 -15 0,6 7 0,9 6 1,1 4 Finn det en korrelation mellan avståndet till skolan och vilken tid man är i skolan?
En graf i LibreOffice ger att \( R^2 = 0,1067\ldots \). Alltså \( R = 0,3266\ldots \).
Eller kommandot =Korrel() ger \( 0,3266\ldots \).
Korrelationen är måttlig. Alltså inte direkt.
- Cecilia och Daniel gjorde ett statistiskt arbete över om det finns ett samband mellan hur många timmar per dygn som man sover och ålder. De intervjuade personer i sin närmsta krets och fick följande data.
Ålder Timmar man sover per dygn. 17 7,5 18 6,5 17 8 15 8,5 47 8,5 48 8,5 55 6,5 57 7,5 67 7,5 84 6 5 10 3 11 12 9 15 8,5 11 8 Finns det ett samband mellan ålder och hur många timmar man sover per dygn?
På LibreOfficeCalc får vi korrelationen till \( -0,6407\ldots \).
Vi har en negativ korrelation. Korrelationen är märkbar. Det betyder att ju äldre man blir destu mindre sover man per dygn.
- Följade uppgift är från korta matematikens studentexamensprov från hösten 2020.
Bedöm på basis av din allmänbildning vilket av alternativen som bäst beskriver korrelationen mellan följande variabler.
Positiv korrelation Korrelationen är nära 0 Negativ korrelation Längd och vikt hos finska barn. Skonummer och blodtryck hos finländska vuxna. Ett lands bruttonationalprodukt per invånare och barndödlighet. Lodräta och vågräta koordinater för pilar som träffat en piltavla. Den rätta raden är
Positiv korrelation Korrelationen är nära 0 Negativ korrelation Längd och vikt hos finska barn. Skonummer och blodtryck hos finländska vuxna. Ett lands bruttonationalprodukt per invånare och barndödlighet. Lodräta och vågräta koordinater för pilar som träffat en piltavla.