7.5. Vinkeln mellan två linjer
Vinkeln mellan två linjer får vi som \( \tan\alpha =\mid\dfrac{k_1-k_2}{1+k_1\cdot k_2}\mid \).

Motivering
I denna motivering används trigonmetri och egenskaper för tangens som behandlas i kurs MaA 7.
Vi utgår från två linjer, \( l_1 \) och \( l_2 \), som har riktingskoefficienterna \( k_1 \) och \( k_2 \). Riktningsvinkeln för \( l_1 \) är \( k_1 = \tan \beta_1 \) och för \( l_2 \) är \( k_2=\tan \beta_2 \).
Vinkeln mellan linjerna beteckar vi med \( \alpha \).
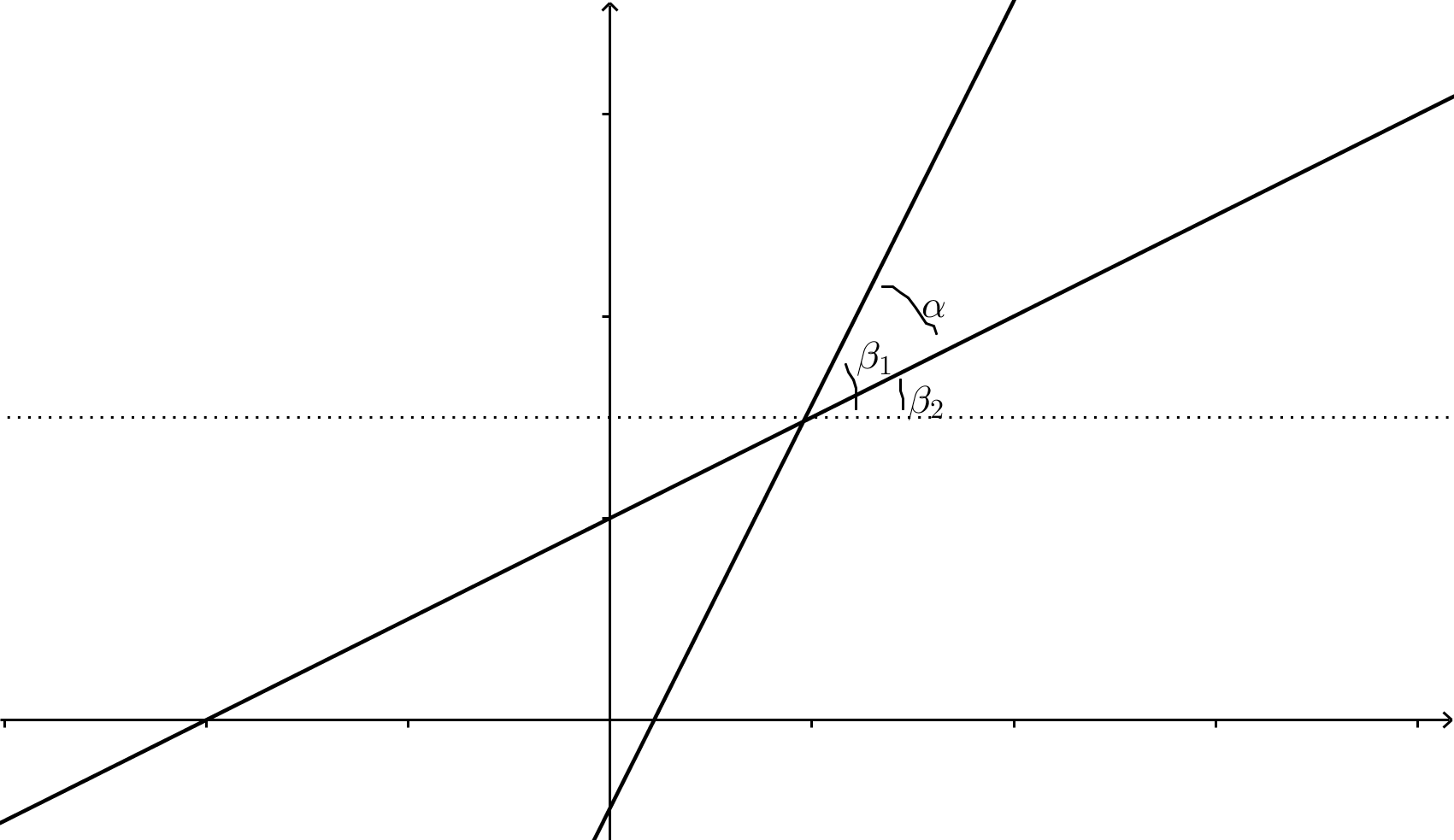
Vi får att \( \alpha = \beta_1 - \beta_2 \). Det betyder att \( \tan \alpha = \tan(\beta_1 - \beta_2) \) . Från trigonometrin finns sambandet \( \tan( x \pm y)= \dfrac{\tan x \pm \tan y}{1 \mp \tan x \tan y} \). Tecknet väljs så att de övre motsvarar och de nedre motsvarar.
Vi får alltså \( \tan \alpha = \dfrac{\tan \beta_1 -\tan \beta_2}{1+\tan \beta_1 \tan \beta_2} \).
Eftersom \( \tan \beta_1 = k_1 \) och \( \tan \beta_2 = k_2 \) får vi \( \tan \alpha = \dfrac{k_1-k_2}{1+k_1 k_2} \).
För att få spetsiga vinklar omger vi kvoten med absolutbelopp.
Vinkeln mellan två linjer är \( \tan \beta_2 = k_2 \) får vi \( \tan \alpha = \mid\dfrac{k_1-k_2}{1+k_1 k_2}\mid \).
Lösning
Vi har \( k_1 = 2 \) och \( k_2=-1 \) och vinkeln får vi via \( \tan\alpha =\mid\dfrac{k_1-k_2}{1+k_1\cdot k_2}\mid \).
Vi får \( \tan \alpha = \mid\dfrac{2-(-1)}{1+2(-1)}\mid = \mid\dfrac{3}{-1}\mid = 3 \).
Vinkeln \( \alpha = 71,56\ldots^{\circ} \approx 71,6^{\circ} \).
Lösning
Vi har att \( k_1=-2 \), \( k_2=a \) och \( \alpha = 60^{\circ} \).
Vi får följande ekvation:
\( \begin{array}{rcl} \tan 60^{\circ} & = & \mid\dfrac{-2-a}{1+(-2)a}\mid \\ \sqrt{3} & = & \mid\dfrac{-2-a}{1-2a}\mid \quad \mid (\quad)^2\\ (\sqrt{3})^2 & = & \dfrac{(-2-a)^2}{(1-2a)^2}\\ 3(1-2a)^2 & = & (-2-a)^2 \\ 3(1-4a+4a^2) & = & 4+4a+a^2 \\ 3-12a+12a^2 & = & 4+4a+a^2 \\ 11a^2 -16a -1 & = & 0 \\ a & = & \dfrac{-(-16)\pm\sqrt{(-16)^2-4\cdot 11 \cdot -1}}{2\cdot 11}\\ \\ & = & \dfrac{16\pm\sqrt{300}}{22} = \dfrac{16\pm10\sqrt{3}}{22}\\ \\ & = & \dfrac{2(8\pm5\sqrt{3})}{22} = \dfrac{8\pm 5\sqrt{3}}{11}\\ \end{array} \)
Då \( a \) har värdet \( \dfrac{8- 5\sqrt{3}}{11} \) eller \( \dfrac{8+ 5\sqrt{3}}{11} \) är vinkeln mellan linjerna \( 60^{\circ} \).
Uppgifter
- Bestäm vinkeln mellan \( y=-3x-1 \) och \( y=x+2 \).
Vi får \( \tan \alpha = \mid \dfrac{-3-1}{1+(-3)\cdot 1} \mid \) som ger oss \( \alpha = 63,4^{\circ} \).
- Bestäm vinkeln mellan \( -3x+y-2=0 \) och \( -4x+y-1=0 \).
Vi får att \( \tan \alpha = \mid \dfrac{3-4}{1+3\cdot 4}\mid \) som ger \( \alpha = 4,3987\ldots\approx 4,4^{\circ} \).
- För vilket värde på \( a \) gäller det att vinkeln mellan \( y=2x-1 \) och \( y=ax+1\dfrac{2}{3} \) har storleken 45o?
Vi får ekvationen \( \tan 45^{\circ}=\mid\dfrac{2-a}{1+2a}\mid \) och \( \tan 45^{\circ}= 1 \). Ekvationen har lösningarna \( a=-3 \) och \( a=\dfrac{1}{3} \).
- För vilket värde på \( a \) gäller det att storleken för vinkeln mellan linjerna \( y=x-1 \) och \( y=ax-4 \) är 30o?
Vi får ekvationen \( \tan 30^{\circ}=\mid\dfrac{x-a}{1+a}\mid \) som har lösningarna \( a=2\pm\sqrt{3} \).
- Bestäm storleken av vinklarna, med en tiondel grads noggrannhet, i triangeln vars hörnpunkter är \( (-3,3) \), \( (1,5) \) och \( (2,1) \).
Vinklarna är \( 48,3^{\circ}, 54,2^{\circ} \) och \( 77,5^{\circ} \).