21. Skalär produkt
Vi börjar med att studera när vektorerna \(\overline{a}=x_1\overline{i}+y_1\overline{j}+z_1\overline{k}\) och \(\overline{b}=x_2\overline{i}+y_2\overline{j}+z_2\overline{k}\) är vinkelräta. Vi gör det via Pythagoras sats.
Vi placerar \(\overline{a}\) och \(\overline{b}\) så att de börjar i samma punkt.
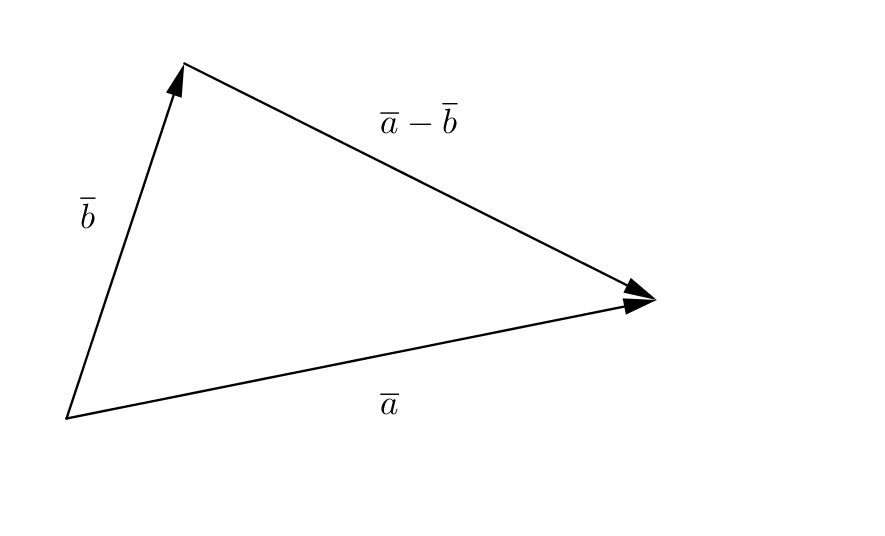
Om triangeln är rätvinklig så gäller att \(\mid \overline{a}-\overline{b} \mid ^2 = \mid \overline{a}\mid ^2 +\mid \overline{b} \mid ^2\).
Vi tar och bildar dessa. \(\mid \overline{a} \mid ^2 = x_1^2 + y_1^2 + z_1^2\) och \(\mid \overline{b} \mid ^2 = x_2^2 + y_2^2 + z_2^2\).
Kvadraten av den tredje längden får vi som
\(\begin{array}{rcl} \mid \overline{a}-\overline{b} \mid ^2\ & = & (x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2 \\ & = & x_1^2-2x_1x_2+x_2^2 + y_1^2-2y_1y_2 + y_2^2 + z_1^2 -2z_1z_2+z_2^2 \\ & = & x_1^2+y_1^2+z_1^2 +x_2^2+y_2^2+z_2^2 -2x_1x_2 -2y_1y_2-2z_1z_2 \\ & = & \mid \overline{a} \mid ^2 + \mid \overline{b} \mid ^2 -2(x_1x_2 + y_1y_2+z_1z_2) \\ \end{array} \)
För att \(\overline{a}\) och \(\overline{b}\) skall vara vinkelräta mot varandra så skall termen \(2(x_1x_2 + y_1y_2+z_1z_2)\) ha värdet noll.
Exempel 1 Är vektorerna \(-\overline{i}+2\overline{j} -2\overline{k}\) och \(4\overline{i}+\overline{j} -\overline{k}\) vinkelräta mot varandra?
Lösning
Jo, eftersom \(-1\cdot 4 + 2\cdot 1 -2(-1)=0\).
Den skalära produkten mellan vektorerna \(\overline{a}=x_1\overline{i}+y_1\overline{j}+z_1\overline{k}\) och \(\overline{b}=x_2\overline{i}+y_2\overline{j}+z_2\overline{k}\) är \(x_1x_2+y_1y_2+z_1z_2\).
Den skalära produkten betecknas \(\overline{a} \cdot \overline{b}\) och utläses "a skalärt b".
Om två vektorer är vinkelräta har den skalära produkten värdet noll.
Exempel 2 Bestäm den skalära produkten för \(\overline{a}=2\overline{i}-\overline{j}\) och \(\overline{b}= -\overline{i}+2\overline{j} -2\overline{k}\).
Lösning
\(\overline{a} \cdot \overline{b}=2(-1) -1\cdot 2 + 0(-2)=-4\).
Exempel 3 Bestäm \(k\) så att \(\overline{a}=3\overline{i}-2\overline{j}\) och \(\overline{b}= k\overline{i}+\overline{j}\) är vinkeräta.
Lösning
Vi får att \(\overline{a}\cdot \overline{b}=0\). Alltså
\(\begin{array}{rcl} 3k-2\cdot1 & = & 0 \\ 3k & = & 2 \\ k & = & \frac{2}{3} \\ \end{array}\)
För den skalära produkten gäller följande egenskaper:
| Kommutativ | \(\overline{a} \cdot \overline{b} = \overline{b} \cdot \overline{a}\) | |
| Distributiv | \(\overline{a} \cdot (\overline{b} +\overline{c}) = \overline{a} \cdot \overline{b} +\overline{a} \cdot \overline{c}\) | Om \(\overline{a}\cdot \overline{b}=2\) och \(\overline{a}\cdot \overline{c}=-4\) så är \(\overline{a}(\overline{b}+\overline{c}) = \overline{a}\cdot \overline{b} + \overline{a}\cdot \overline{c} = 2+(-4)=-2\). |
| Utflyttning av koefficienter | \((s\overline{a}) \cdot \overline{b} = \overline{a} \cdot (s\overline{b}) = s(\overline{a} \cdot \overline{b})\) | Om \(\overline{a} \cdot \overline{b} = 5\) så är \((-4\overline{a}) \cdot \overline{b} = -4(\overline{a} \cdot \overline{b}) = -4 \cdot 5 = -20\) och \(2\overline{a} \cdot (-3\overline{b}) = 2\cdot(-3)(\overline{a} \cdot \overline{b})=-6 \cdot (-5)=30\). |
| Punktprodukten | \(\overline{a}\cdot \overline{a} = \mid \overline{a} \mid^2\) | Punktprodukten av \(\overline{a}\cdot \overline{a}\) ger längden av \(\overline{a}\) i kvadrat. |
Uppgifter
- Bestäm den skalära produkten för
- \(3\overline{i}+\overline{j}\) och \(\overline{i}+2\overline{j}\).
\( 3 \cdot 1 + 1 \cdot 2 = 5 \)
- \(3\overline{i}-\overline{j}\) och \(-3\overline{i}+\overline{j}\).
\( 3(-3) + -1\cdot 1 = -10\)
- \(2\overline{i}\) och \(\overline{i}+2\overline{j}\).
\( 2 \cdot 1 + 0 \cdot 2 = 2\)
- \(3\overline{i}+\overline{j}\) och \(\overline{i}+2\overline{j}\).
- Från hörnet i en triangel börjar följande vektorer. Bestäm om triangeln är rätvinklig.
- \( \overline{a} = 3\overline{i} + 2\overline{j} \) och \( \overline{b} = 2\overline{i} -3 \overline{j} \).
Den skalära produkten mellan \( \overline{a} \cdot \overline{b} = 3\cdot 2 +2(-3) = 0 \). Vinkeln mellan vektorerna är rät.
Triangeln är rätvinklig.
- \( \overline{a} = 4\overline{i} - 2\overline{j} \) och \( \overline{b} = \overline{i} -8 \overline{j} \).
Den skalära produkten mellan \( \overline{a} \cdot \overline{b} = 4\cdot 1 -2(-8) = 20 \). Vinkeln mellan vektorerna är inte rät.
Den tredje sidan \( \overline{c} = -\overline{a} + \overline{b} = -3\overline{i} -6\overline{j} \) eller \( \overline{a} - \overline{b} \).
\( \overline{a} \cdot \overline{c} = 4(-3) -2(6) = 0 \). Vinkeln mellan vektorerna är rät.
Triangeln är rätvinklig.
- \( \overline{a} = 2\overline{i} +2\overline{j} +4\overline{k} \) och \( \overline{b} = -3\overline{i} - \overline{j} +2\overline{k} \).
Den skalära produkten mellan \( \overline{a} \cdot \overline{b} = 2(-3) +2(-1)+4\cdot 2 = 0 \). Vinkeln mellan vektorerna är rät.
Triangeln är rätvinklig.
- \( \overline{a} = 3\overline{i} + 2\overline{j} \) och \( \overline{b} = 2\overline{i} -3 \overline{j} \).
- Är triangeln som består av vektorerna \(\overline{a}=\overline{i}-\overline{j}\), \(\overline{b}=-3\overline{i}-5\overline{j}\) och skillnaden av dessa rätvinklig?
Ja. Vi bestämmer de skalära produkterna. Vi behöver \( \overline{c} = \overline{a}-\overline{b}= 4\overline{i} +4\overline{j}\).
\( \overline{a} \cdot \overline{b} = 1\cdot(-3)+(-1)(-5) = 2\). Dessa är inte vinkelräta.
\( \overline{a} \cdot \overline{c} = 1\cdot 4 +(-1)\cdot 4 = 0\). Dessa är vinkelräta.
\( \overline{b} \cdot \overline{c} = -3\cdot 4 +(-5)\cdot 4 = -32\). Dessa är inte vinkelräta.
Eftersom vi har en triangel så räcker det med att hitta en rät vinkel.
- Är triangeln ABC som bestäms av punkterna \((-2,2)\), \((-1,5)\) och \((4,0)\) rätvinklig?
Det räcker att hitta en rät vinkel.
Vi bilar vektorerna mellan punkterna, \(A=(-2,2)\), \(B=(-1,5)\) och \(C=(4,0)\)
\( \overrightarrow{AB} = (-1-(-2))\overline{i} + (5-2)\overline{j} = \overline{i} + 3\overline{j} \).
\( \overrightarrow{AC} = (4-(-2))\overline{i} + (0-2)\overline{j} = 6 \overline{i} - 2\overline{j} \).
\( \overrightarrow{BC} = (4-(-1))\overline{i} + (0-5)\overline{j} = 5 \overline{i} - 5\overline{j} \).
Vi bilar de skalära produkterna.
\( \overrightarrow{AB} \cdot \overrightarrow{AC} = 1\cdot 6 +3(-2) = 0 \). Här är en rät vinkel. (Eftersom vi har hittat den behöver vi inte undersöka de andra.)
\( \overrightarrow{AB} \cdot \overrightarrow{BC} = 1\cdot 5 +3(-5) = -10 \).
\( \overrightarrow{AC} \cdot \overrightarrow{BC} = 6\cdot 5 -2(-5) = 40 \).
Ja, triangeln är rät vinkel vid punkten \( (-2,2) \).
- För vilka värden på \(k\) gäller att triangeln som bestäms av punkterna \((-4,1)\), \((k,4)\) och \((-3,6)\) är rätvinklig.
Vi bildar vektorerna mellan punkterna \(A=(-4,1)\), \(B=(k,4)\) och \(C=(-3,6)\).
\( \overrightarrow{AB} = (k-(-4))\overline{i} + (4-1)\overline{j} = (k+4)\overline{i} + 3\overline{j} \).
\( \overrightarrow{BC} = (-3-k)\overline{i} + (6-4)\overline{j} = (-3-k)\overline{i} +2\overline{j} \).
Eftersom \( k \) endast finns i en punkt klarar vi oss med dessa vektorer. Vi bildar den skalära produkten och tvingar att ha värdet 0.
\( \begin{array}{rcl} \overrightarrow{AB} \cdot \overrightarrow{BC} & = & 0 \\ (k+4)(-3-k)+3\cdot 2 & = & 0 \\ \end{array} \)
Ekvationen har lösningarna \( k_1 = -6 \) och \( k_2 = -1 \).
- Bestäm för linjen \(2x-6y-6=0\)
- en riktningsvektor
\( 2x-6y -6 = 0 \Leftrightarrow y = \dfrac{1}{3}x +1 \).
Riktningsvektorerna är \(3\overline{i}+\overline{j}\) eller \(-3\overline{i}-\overline{j}\) och multiplar av dessa.
- en normalvektor (en vektor som bildar en normal)
Eftersom linjens riktningskoefficient är \( \dfrac{1}{3} \) så är normalens riktningskoefficient \( -3 \). (Produkten skall ha värdet \( -1 \).)
Riktningsvektorerna är \(-\overline{i}+3\overline{j}\) eller \(\overline{i}-3\overline{j}\) och multiplar av dessa.
- en normalvektor vars längd är 1
Vi söker enhetsvektorn för normalvektorn, \( \overline{n}^0 = \dfrac{1}{\mid \overline{n} \mid }\cdot \overline{n} \).
Längden av vektorn \( -\overline{i}+3\overline{j} \) är \( \sqrt{(-1)^2+3^2} = \sqrt{10} \).
Normalvektorns enhetsvektor är \(\dfrac{1}{\sqrt{10}}(-\overline{i}+3\overline{j})\) eller \(\dfrac{1}{\sqrt{10}}(\overline{i}-3\overline{j})\).
- en normalvektor vars längd är 10.
Längden av de vektorer som vi bestämde i c) har längden 1. Vi gör dem 10 ggr längre.
Vi får \(\dfrac{10}{\sqrt{10}}(-\overline{i}+3\overline{j}) = \sqrt{10}(-\overline{i}+3\overline{j})\) eller \(\sqrt{10}(\overline{i}-3\overline{j})\).
- en riktningsvektor
- Om vektorn \( \overline{a} \) som finns i \( xy \)-planet vet vi att \( \overline{a} \cdot \overline {i} = 3 \) och att \( \overline{a} \cdot \overline {j} = 6 \). Bestäm vektorn \( \overline{a} \).
Vi betecknar \( \overline{a} = x\overline{i} + y\overline{j} \). De skalära produkterna ger oss ekvationerna \( x\cdot 1 + y\cdot 0 = 3 \) och \( x\cdot 0 + y\cdot 1 = 6 \) ger oss lösningarna.
Alltså \( \overline{a} = 3\overline{i} + 6\overline{j} \).
- Hitta i alla fall fyra vektorer som alla har olika längd som är vinkelräta mot \(\overline{a}=\overline{i}+2\overline{j}+\overline{k}\).
Vektorerna är av typ \( \overline{b} = x\overline{i} + y\overline{j} + z\overline{k} \).
Då \( \overline{a} \) och \( \overline{b} \) skall vara vinkelräta skall den skalära produkten ha värdet 0.
Vi får \( 1\cdot x +2\cdot y +1\cdot z =0 \).
Testa dig fram (;
Tex: \(-\overline{j}+2\overline{k}\), \(\overline{i}-\overline{k}\), \(-4\overline{i}+2\overline{j}\) och \(-4\overline{i}+\overline{j}+2\overline{k}\).
- Låt \( \overline{a} = \overline{i} + 2\overline{j} + \overline{k} \) och \( \overline{b} = s\overline{i} + \overline{j} - \overline{k} \). Bestäm \( s \) så att vektorerna \( \overline{a} + \overline{b} \) och \( \overline{a} - \overline{b} \) är vinkelräta mot varandra.
Bilda vektorerna \( \overline{a} + \overline{b} = (1+s)\overline{i} + 3\overline{j} \) och \( \overline{a} - \overline{b} = (1-s)\overline{i} + \overline{j} +2\overline{k}\).
Bilda skalära produkten av dessa och låt den få värdet 0.
Kom fram till \( s = 2 \) eller \( s = -2 \).
- För vilka punkter på \( z \)-axeln gäller att sträckan mellan \( A=(4,1,2) \) och \( B=(-5,6,-3) \) syns ur en rät vinkel?
Punkterna på \( z \)-axeln är av formen \( P=(0,0,z) \).
Bilda vektorerna \( \overline{PA} \) och \( \overline{PB} \). Utnyttja sedan att skalära produkten skall ha värdet 0.
Punkterna är \( (0,0,4) \) och \( (0,0,-5) \).
- I triangeln \( ABC \) gäller att \( \overline{AB} \cdot \overline{CB} = \overline{BA} \cdot \overline{CA} \). Visa att sidorna \( BC \) och \( AC \) är lika långa.
Till exempel på följande sätt.
Vi betecknar \( \overrightarrow{AB} = \overline{a} \) och \( \overrightarrow{AC} = \overline{b} \), då är \( \overrightarrow{CB} = \overline{a}-\overline{b} \).
\( \overline{AB} \cdot \overline{CB} = \overline{a} \cdot (\overline{a}-\overline{b}) \).
\( \overline{BA} \cdot \overline{CA} = -\overline{a} \cdot -\overline{b} \).
\( \overline{AB} \cdot \overline{CB} = \overline{BA} \cdot \overline{CA} \) är samma som \( \overline{AB} \cdot \overline{CB} - \overline{BA} \cdot \overline{CA} = 0 \), alltså \( \overline{a} \cdot (\overline{a}-\overline{b}) - (-\overline{a} \cdot -\overline{b}) = 0 \).
Alltså
\( \begin{array}{rcll} \mid \overline{a} \mid^2 -2(\overline{a} \cdot \overline{b}) & = & 0 & \mid + \mid \overline{b}\mid^2 \\ \mid \overline{a} \mid^2 -2(\overline{a} \cdot \overline{b}) +\mid \overline{b}\mid^2 & = & \mid \overline{b}\mid^2 \\ (\overline{a}-\overline{b})^2 & = & (\overline{b})^2 \\ \overline{a}-\overline{b} & = & \overline{b} \\ \end{array} \)
Alltså är \( BC \) lika lång som \( AC \).