3. Kvadreringsregeln
Vi förenklar följande uttryck tillsammans:
- \((2+x)^2\)
- \((a+b)^2\)
- \((-1+a)^2\)
För att enkelt förenkla kvadraten av ett binom, \((a+b)^2\) använder vi oss av kvaderingsregeln. Kvadreringsregel skriver vi som \((a+b)^2=a^2+2ab+b^2\). Ibland ser man även \((a-b)^2=a^2-2ab+b^2\). En del trinom kan vi skriva som kvadrater, faktorisera med hjälp av kvadreringsregeln, tex \(x^2-4x+4\) som \((x^2-2)^2\).
Exempel 1 Fyll i så att det blir rätt:
- \((x\underline{\qquad})^2 = x^2 -4x\underline{\qquad\qquad}\)
- \((2x\underline{\qquad})^2 = 4x^2 + x \underline{\qquad}\)
Kvadrering av ett binom räknar vi som
\((a+b)^2 = a^2+2ab+b^2\).
Uppgifter
- Berätta om fördelen med kvadreringsregeln.
Vi kan på ett lätt sätt kvadrera ett binom.
- Kombinera så att det blir rätt.
Välj bland följande uttryck:
\((x-3)^2\)\((x-2)^2\)\((x-1)^2\)\((x+1)^2\)\((x+2)^2\)\((x+3)^2\)Uttryck Motsvarande uttryck \(x^2+4x+4\) \(x^2-4x+4\) \(x^2+2x+1\) \(x^2-2x+1\) \(x^2+6x+9\) \(x^2-6x+9\) Uttryck Motsvarande uttryck \((x+2)^2\) \(x^2+4x+4\) \((x-2)^2\) \(x^2-4x+4\) \((x+1)^2\) \(x^2+2x+1\) \((x-1)^2\) \(x^2-2x+1\) \((x+3)^2\) \(x^2+6x+9\) \((x-3)^2\) \(x^2-6x+9\) - Kvadrera följande uttryck
- \((2+n)^2 \)
\((2+n)^2 = n^2+4n +4 \)
- \((3-n)^2 \)
\((3-n)^2 = 9-6n+n^2 \)
- \((x-y)^2 \)
\((x-y)^2=x^2-2xy+y^2 \)
- \((2+n)^2 \)
- Kvadrera
- \((x+\dfrac{1}{4})^2 \)
\((x+\dfrac{1}{4})^2 = x^2 +\dfrac{1}{2}x+\dfrac{1}{16} \)
- \((x-2y)^2 \)
\((x-2y)^2 = x^2-4xy+4y^2 \)
- \((\dfrac{1}{3}-b)^2 \)
\((\dfrac{1}{3}-b)^2 = \dfrac{1}{9}-\dfrac{2b}{3}+b^2 \)
- \((x+\dfrac{1}{4})^2 \)
- Kvadrera
- \((m-\sqrt{2})^2 \)
\((m-\sqrt{2})^2 = m^2-2\sqrt{2}m+2 \)
- \((\dfrac{1}{2}x-2)^2 \)
\((\dfrac{1}{2}x-2)^2 = \dfrac{1}{4}x^2 -2x +4 \)
- \((2a-5b)^2 \)
\((2a-5b)^2 = 4a^2-20ab+25b^2 \)
- \((m-\sqrt{2})^2 \)
- Fyll i fältet så att det blir rätt. Glöm inte tecknet framför talet!
- \((x \underline{\qquad} )^2 = x^2 +12x \underline{\qquad} \)
\((x \underline{+6})^2 = x^2 +12x \underline{+36} \)
- \((x \underline{\qquad})^2 = x^2 -16x \underline{\qquad} \)
\((x \underline{-8})^2 = x^2 -16x \underline{+64} \)
- \((x \underline{\qquad} )^2 = x^2 +x \underline{\qquad} \)
\((x \underline{+\dfrac{1}{2}} )^2 = x^2 +x \underline{+\dfrac{1}{4}} \)
- \((x \underline{\qquad} )^2 = x^2 -4x \underline{\qquad} \)
\((x \underline{-2} )^2 = x^2 -4x \underline{+4} \)
- \((x \underline{\qquad} )^2 = x^2 +12x \underline{\qquad} \)
- Fyll i så att det blir rätt.
- \((\underline{\qquad})^2 = \underline{\qquad} 2x+1 \)
\((\underline{\pm x \pm 1})^2 = \underline{x^2} \pm 2x+1\)
Tecket måste vi välja så att bägge \( x \) och \( 1 \) har samma tecken.
- \((\underline{\qquad})^2 = 4x^2 \underline{\qquad} \dfrac{1}{4} \)
\((\underline{\pm 2x\pm \dfrac{1}{2}})^2 = 4x^2 \underline{\pm 2x} +\dfrac{1}{4}\)
Här är det ingen skillnad hur vi väljer teckena.
- \((\underline{\qquad}x\underline{\qquad})^2 = 2x^2 + x \underline{\qquad} \)
\((\underline{\pm \sqrt{2}}x\underline{\pm \dfrac{1}{2\sqrt{2}}})^2 = 2x^2 + x +\underline{\dfrac{1}{8}}\)
Här måste vi välja tecknena så att bägge, \( \sqrt{2}x \) och \( \dfrac{1}{2\sqrt{2}} \) har samma tecken.
- \((\underline{\qquad}x\underline{\qquad})^2 = 4x^2 - 4 x \underline{\qquad} \)
\((\underline{\pm 2}x\underline{\pm 1})^2 = 4x^2 - 4 x \underline{+1}\)
Här måste vi välja teckn så att de är motsatta.
- \((\underline{\qquad})^2 = \underline{\qquad} 2x+1 \)
- Skriv som en kvadrat.
- \(x^2+6x+9\)
\(x^2+6x+9 = (x+3)^2\)
- \(x^2-2x+1\)
\(x^2-2x+1 = (x-1)^2\)
- \(16x^2+4x+\dfrac{1}{4}\)
\(16x^2+4x+\dfrac{1}{4} = (4x+\dfrac{1}{2})^2\)
- \(4x^2-8x+4\)
\(4x^2-8x+4 = (2x-2)^2\)
- \(x^4-8x^2+16\)
\(8x^2+16 = (x^2-4)^2\)
- \(x^2+6x+9\)
- Lös följande ekvationer.
- \( (x+3)^2 = x^2+9 \)
Vi får
\( \begin{array}{rcl} (x+3)^2 & = & x^2+9 \\ x^2 +6x +9 & = & x^2+9 \\ 6x & = & 0 \\ x & = & 0 \\ \end{array} \)
- \( (x-5)^2 = x^2-25 \)
Vi får
\( \begin{array}{rcl} (x-5)^2 & = & x^2-25 \\ x^2 -10x +25 & = & x^2-25 \\ -10x & = & -50 \\ x & = & 5 \\ \end{array} \)
- \( (x-2)^2 = x^2-4x \)
Vi får
\( \begin{array}{rcl} (x-2)^2 & = & x^2-4x \\ x^2 -4x +4 & = & x^2-4x \\ 0 & = & 4 \\ \end{array} \)
Ekvationen saknar lösningar.
- \( (x+3)^2 = x^2+9 \)
- Förklara kvaderingsreleln geometriskt genom att utnyttja areorna i följande figurer.
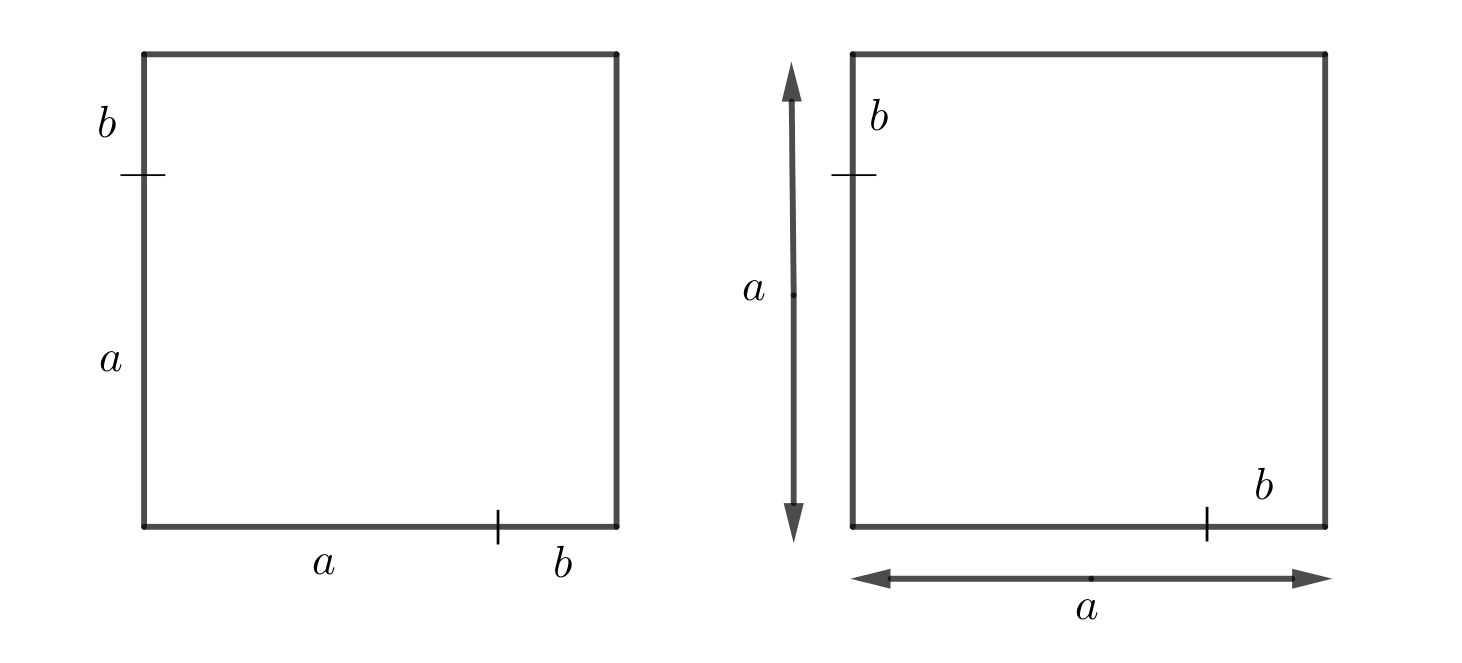
\( (a+b)^2 = a^2+2ab+b^2 \) och \( (a-b)^2 = a^2-2ab+b^2 \)
Vi ritar in följande linjer.
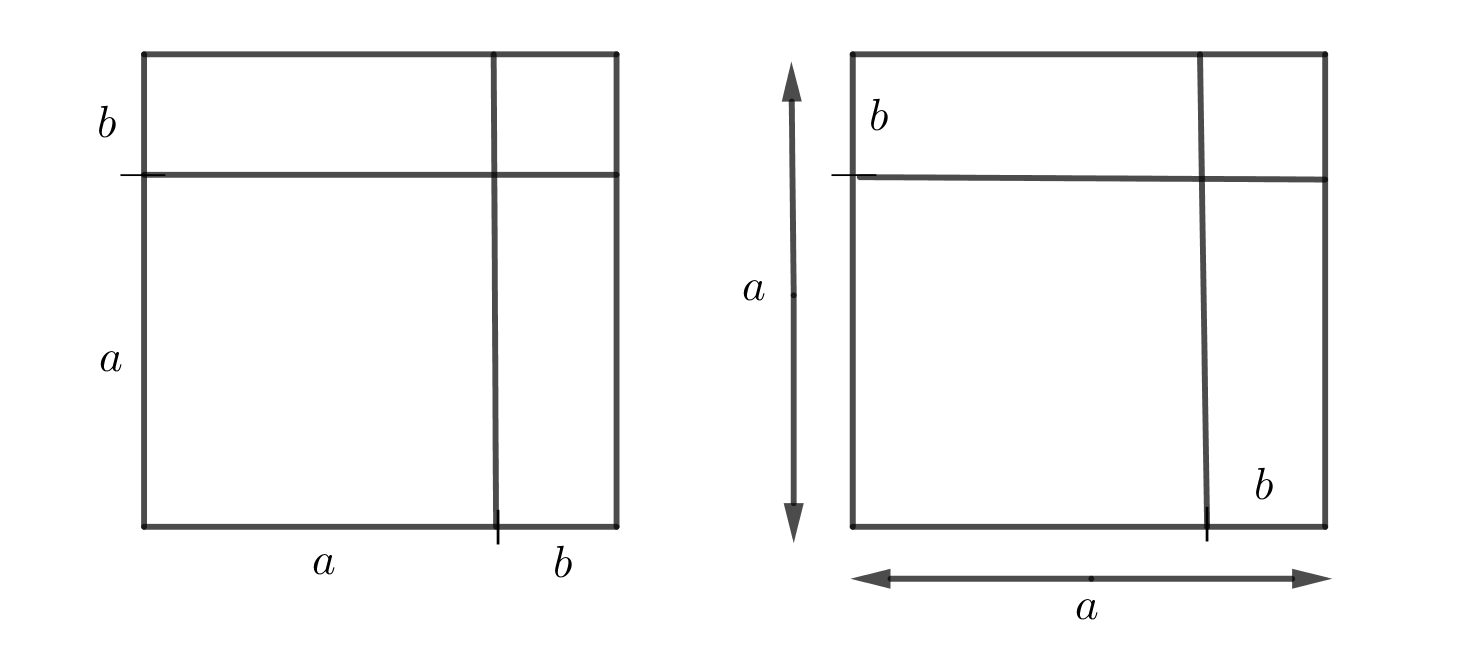
För \( (a+b)^2 \) märker vi att den består av fyrhörningarna \( a^2 \), \( ab \), \( ab \) och \( b^2 \). Alltså \( a^2 +2ab +b^2 \).
För den andra kvadraten med sidan \( a \) är arean \( a^2 \). Den består av fyrhörningarna \( (a-b)^2 \), \(a-b)\cdot b \), \(a-b)\cdot b \) och \( b^2 \).
Vi får att \( a^2 = (a-b)^2 + 2b(a-b) + b^2 \). När du förenklar detta får du \( (a-b)^2 = a^2-2ab+b^2 \).