MaA 2 Polynomekvationer och -funktioner

10. Parabeln - grafen av en andragradsfunktion

Grundformen för en andragradsfunktion ser ut som \(f(x)= ax^2 +bx+c\). \(a\), \(b\) och \(c\) påverkar olika på hur funktionen ser ut. Vi kallar grafen av en andragradsfunktion för en parabel.

Testa själv genom att ändra på värdet för \(a\), \(b\) och \(c\). Vad märker du?

  • \(a\) inverkar på hur brant funktionen öppnar sig. Är \(a > 0\) öppnar sig parabeln uppåt. Är \(a < 0\) öppnar sig parabeln nedåt.
  • \(b\) flyttar parabeln i sidled och
  • \(c\) flyttar parabeln i höjdled.
Exempel 1 Bestäm funktionsvärdena \(f(-2)\) för funktionen \(f(x)=-2x^2-3x-1\).

Lösning

Funktionsvärdet får vi genom att sätta in värdet i funktionen.

\(f(-2) = -2(-2)^2-3(-2)-1 = -3\).

Exempel 2 Bestäm nollställena för \(f(x)= -x^2+6x-5\). Bestäm koordinaten för toppen för parabeln.

Lösning

Vi löser nollställena: \(-x^2+6x-5 = 0\).

\(\begin{array}{rcll} x & = & \dfrac{-6 \pm \sqrt{6^2-4(-1)(-5)}}{2\cdot (-1)} \\ x & = & \dfrac{-6 \pm \sqrt{16}}{-2} \\ x = \dfrac{-6-4}{-2}=5 & \textrm{ eller } & x=\dfrac{-6+4}{-2}=1 \\ \end{array} \)

Nollställena är i \(x_1=1\) och \(x_2=5\).

Toppen finner vi mitt emellan nollställena: \(\dfrac{5-1}{2} = 3\).

Y-koordinaten är: \(f(3) = -3^2+6\cdot 3-5 = 4\).

Toppens koordinater är \((3,4)\).

Toppen är den punkt där parabeln byter riktning. Toppen för en parabel finns mitt mellan nollställena.

Vill du räkna ut \(x\)-koordinaten räknar du ut den via \(\dfrac{\dfrac{-b-\sqrt{b^2-4ac}}{2a} + \dfrac{-b+\sqrt{b^2-4ac}}{2a}}{2} = -\dfrac{b}{2a} \).

Exempel 3 Bestäm på Geogebra ekvationen för vajrarna som spänner upp Golden Gate bron från San Francisco till Marin County i Kalifornien, USA .

För att bestämma funktionen gör du följande.

  • Importera bilden i GeoGebra.
  • Markera några punkter på kurvan som du vill ha. Ingen panik, man kan alltid flytta på punkterna.
  • I Inmatningsfältet eller CAS använder du dig av RegressionPoly({A,B,C},2), eller FitPoly för att bestämma funktionen.

Uppgifter

  1. Kombinera rätt funktion med rätt graf.

    Försök att fundera dig fram till rätt lösning. Fundera hur koefficienterna \( a \), \( b \) och \( c \) påverkar grafen av parabeln, \( y = ax^2 +bx +c \).

    Vilken koefficient ändrar på hur brett parabeln öppnar sig? Vilken koefficeint flyttar parabeln i sidled? Vilken koefficient flyttar på parabeln uppåt och nedåt?

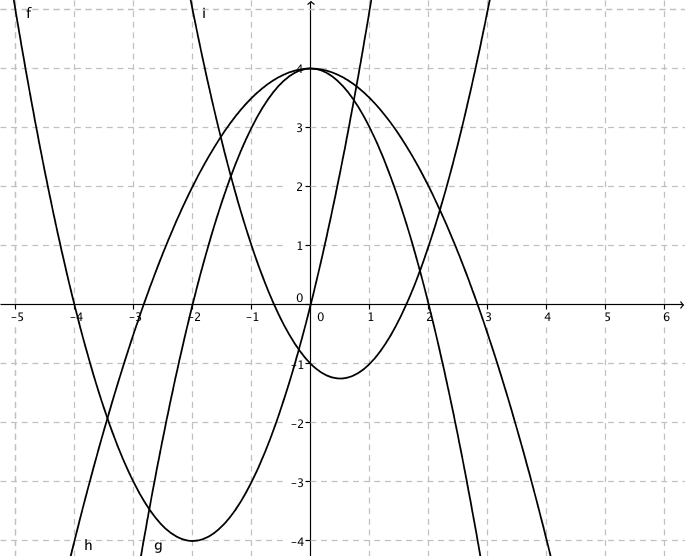
    Välj bland följande:

    \(f(x)\)
    \(g(x)\)
    \(h(x)\)
    \(i(x)\)

    FunktionUttryck
    \(x^2+4x\)
    \(-x^2+4\)
    \(-\dfrac{1}{2}x^2+4\)
    \(x^2-x-1\)

    FunktionUttryck
    \(f(x)\)\(x^2+4x\)
    \(g(x)\)\(-x^2+4\)
    \(h(x)\)\(-\dfrac{1}{2}x^2+4\)
    \(i(x)\)\(x^2-x-1\)
  2. Bestäm funktionsvärdena \(f(-1)\) och \(f(2)\) för \(f(x)= -x^2-3x+1\).

    Vi får \(f(-1)=-(-1)^2-3(-1) +1 = 3\) och \(f(2)=-2^2-3\cdot 2+1 = -9\).

  3. Bestäm för följande funktioner om grafen är funktionen är en parabel. Om det är en parabel så bestäm om den öppnar sig uppåt eller nedåt.
    FunktionParabelInte parabelÖppnar sig uppåtÖppnar sig nedåt
    \( f(x) = x^2-3x \)
    \( f(x) = -3x^2 +2 \)
    \( f(x) = x^3+x^2 \)
    \( f(x) = x(x-1)+3 \)
    \( f(x) = 3(4-x^2) \)
    \( f(x) = x^2(x+2) \)

    Vi får följande

    FunktionParabelInte parabelÖppnar sig uppåtÖppnar sig nedåt
    \( f(x) = x^2-3x \)
    \( f(x) = -3x^2 +2 \)
    \( f(x) = x^3+x^2 \)
    \( f(x) = x(x-1)+3 \)
    \( f(x) = 3(4-x^2) \)
    \( f(x) = x^2(x+2) \)
  4. Bestäm nollställen för följande funktioner.
    1. \(f(x)= x^2-4x-5\)

      Ekvationen \(f(x)=x^2-4x-5=0\) ger \(x_1=-1\) och \(x_2=5\).

    2. \(g(x)=x^2-4x\)

      Ekvationen \(g(x)=x^2-4x=0\) ger \(x_1=0\) och \(x_2=4\).

    3. \(h(x)=x^2+4x+3\)

      Ekvationen \(h(x)=x^2+4x+3\) ger \(x_1=-3\) och \(x_2=-1\).

  5. Bestäm

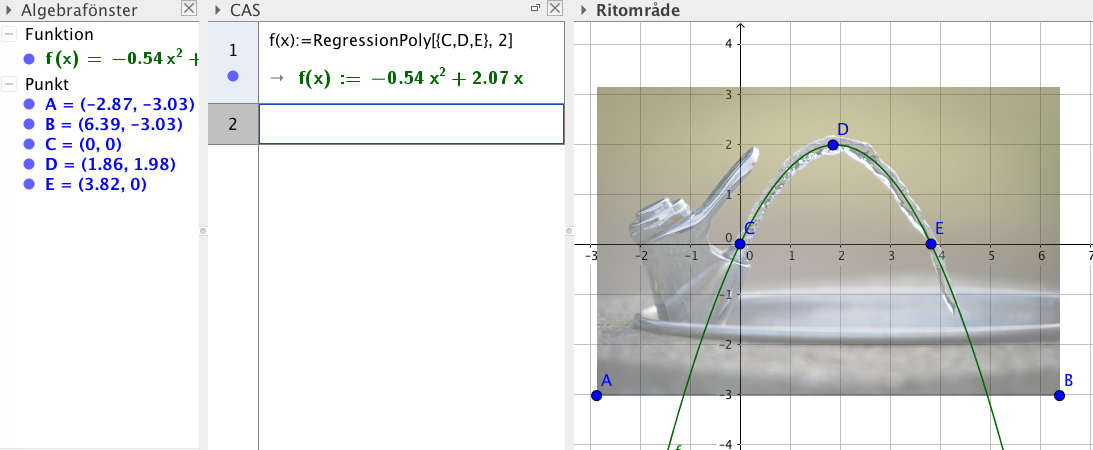
    1. ekvationen för parabeln som beskriver vattenstrålen från dricksfontänen. Bild

      Lite beroende på hur man väljer men något i stil med

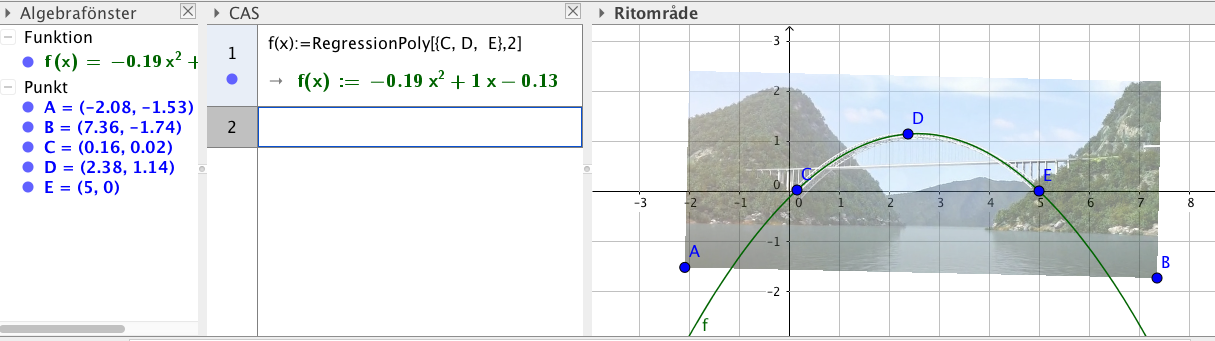
    2. ekvationen för parabeln som beskriver brospannet för Xiangxi bron i Xiangxizhen, Hubei, Kina.Bild

      Lite beroende på hur man väljer men något i stil med

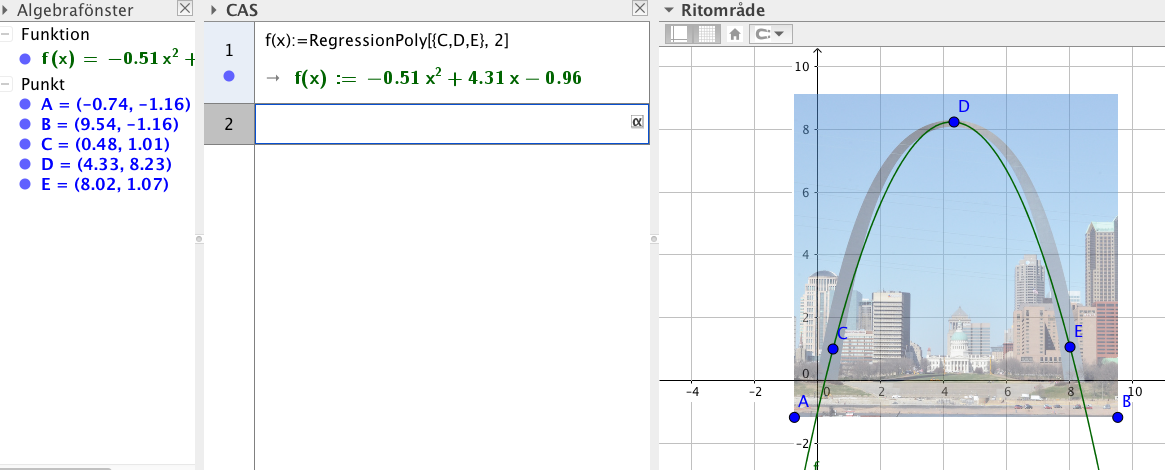
    3. ekvationen för parabeln som beskriver Eero Saarinens konstverk Gateway Arch i Saint Louis, USA. Bild

      Lite beroende på hur man väljer men något i stil med

    4. ekvationen för parabeln som beskriver hålet i Doulbe O Arch i Arches National Pari, Utah, USA. Bild

      Lite beroende på hur man väljer men något i stil med

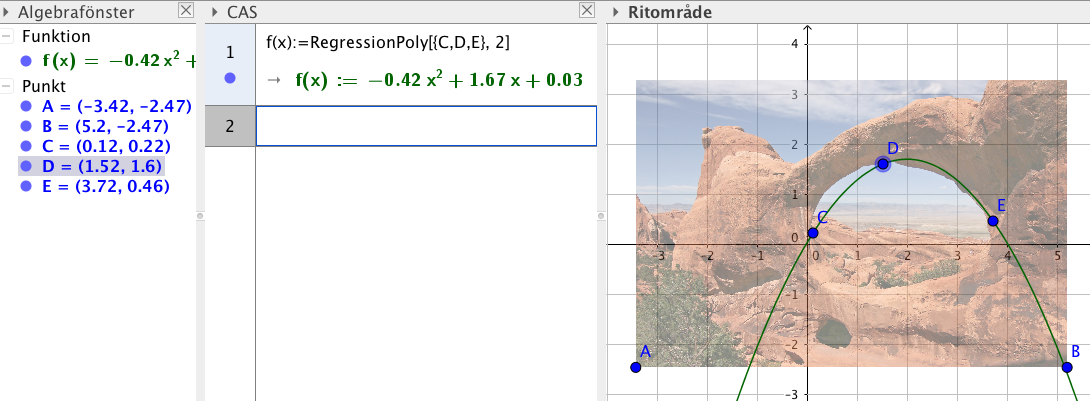
  6. Bestäm toppens koordinat för

    Toppen hittar du mitt mellan nollställena. Gå via nollställena eller så direkt med formel.
    1. \(f(x)= x^2-2x\)

      Nollställena är \(x^2-2x=0 \Leftrightarrow x=0\) och \(x=2\). Toppen finns mitt emellan dessa, alltså då \(x=1\).

      \(y\)-koordinaten är \(f(1)=1^2-2\cdot1 = -1\).

      Toppens koordinat är \((1,-1)\).

    2. \(g(x)= x^2-2x-8\)

      \(g(x)= x^2-2x-8 =0\) då \(x=-2\) och \(x=4\).

      Toppens \(x\)-koordinat hittar vi mitt emellan \(\dfrac{-2+4}{2}=1\).

      \(y\)-koordinaten är \(f(1)=1^2-2\cdot 1-8 = -9\).

      Toppens koorinat är \((1,-9)\).

    3. \(h(x)=-x^2 +6x+7\)

      \(h(x)=-x^2 +6x+7 =0\) då \(x=-1\) och \(x=7\).

      Toppens \(x\)-koordinat hittar vi i \(\dfrac{-1+7}{2}=3\).

      \(y\)-koordinaten är \(f(3)=-3^2+6\cdot 3+7 = 16\).

      Toppen koordinat är i \((3,16)\).

  7. För vilket värde på variablen \( t \) gäller att funktionsvärdena för \( f(t) = 4t^2-t-5 \) och \( g(t) = t^2-t+7 \) är samma. Vilka är dessa funktionsvärden?

    Vi skall lösa ekvationen \( f(t) = g(t) \).

    Alltså \( 4t^2 -t-5 = t^2-t+7 \). Vi löser med rotformlen och får lösningarna \( t_1 = -2 \) och \( t = 2 \).

    Då \( t = -2 \) har bägge funktionerna funktionsvärdet \( f(-2) = 13 \), och då \( t = 2 \) har bägge funktionerna funktionsvärdet \( f(2) = 9 \).

  8. I vilka punkter skär \(f(x)=-x^2-x+6\) \(x\)-axeln?

    \(x\)-koordinaterna för skärningspunkterna hittar vi genom att bestämma nollställena. Alltså \(-x^2-x+6=0\) som har lösningarna \(x=2\) och \(x=-3\).

    För skärningspunkterna gäller att \(y\)-koordinaten har värdet 0.

    Skärningspunkterna är \((2,0)\) och \((-3,0)\).

  9. I vilka punkter skär \( f(x)=x^2+2x-3 \) \(x\)-axeln?

    \(x\)-koordinaterna för skärningspunkterna hittar vi genom att bestämma nollställena. Alltså \(x^2+2x-3=0\) som har lösningarna \(x_1 = -3 \) och \( x = 1 \).

    För skärningspunkterna gäller att \(y\)-koordinaten har värdet 0.

    Skärningspunkterna är \((-3,0)\) och \((1,0)\).

  10. I vilken punkt skär \(f(x)=x^2-4x-5\) \(y\)-axeln?

    Då funktionen skär \(y\)-axeln gäller det att \(x\)-koordinaten har värdet 0. Vi får att \(f(0)=-5\).

    Punkten är \((0,-5)\).

  11. I vilken punkt skär \( f(x) = x^2-7x+6 \) \(y\)-axeln?

    Då funktionen skär \(y\)-axeln gäller det att \(x\)-koordinaten har värdet 0. Vi får att \(f(0)=6\).

    Punkten är \((0,6)\).

  12. En parabel går genom punkterna \((-1,0)\), \((0,-5)\) och \((2,-9)\). Bestäm uttrycket för funktionen.

    Lös uppgiften utan att använda dig av räknare eller räknarprogram. Du kan kolla lösningen på räknare eller räknarprogram. Ekvationssystemet kan du lösa på räknare om du vill.

    En andragradsfunktion ser ut som \(f(x)=ax^2+bx+c\). Bilda ett ekvationssystem och lös det.

    Vi får ekvationssystemet

    \(\left\{ \begin{array}{rcl} a(-1)^2+b(-1)+c & = & 0 \\ a\cdot 0 + b\cdot 0 + c & = & 5 \\ a\cdot2^2+b\cdot 2+c & = & -9 \\ \end{array} \right.\)

    Som har lösningarna \(a=1\), \(b=-4\) och \(c=-5\).

    Funktionen är \(f(x)=x^2-4x-5\).