MaA 12 Algoritmer i matematiken

8. Repetition

Här hittar du sådant som fungear som repetionsuppgifter.

För att kunna programmera med Python på egen dator behöver du ha Python installerat på den. Följ instruktionerna på tie.koodariksi.fi för att installera Python eller så jobbar du på Replit.com.

Uppgifter

  1. Bestäm följande kvoter.
    1. \( \dfrac{x^3+4x^2+3x}{x+1} \)

      Vi får

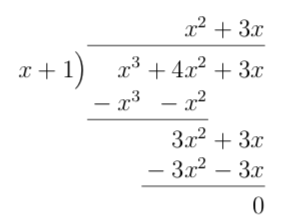
      Alltså \( \dfrac{x^3+4x^2+3x}{x+1} = x^2+3x \).

    2. \( \dfrac{2x^3+12x^2-2x-60}{x+5} \)

      Vi får

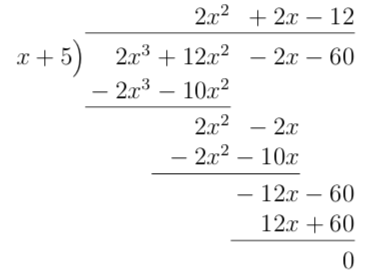
      Alltså \( {2x^3+12x^2-2x-60}{x+5} = 2x^2+2x-12 \).

    3. \( \dfrac{x^3-x^2-8x+9}{x+3} \)

      Vi får

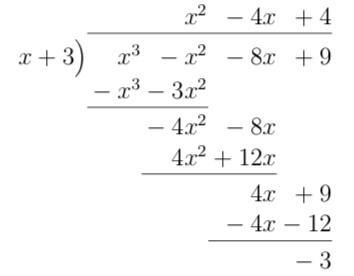
      Alltså \( \dfrac{x^3-x^2-8x+9}{x+3} = x^2 -4x +4 -\dfrac{3}{x+3} \).

    4. \( \dfrac{4x^4+7x^2+2}{x-2} \)

      Vi får

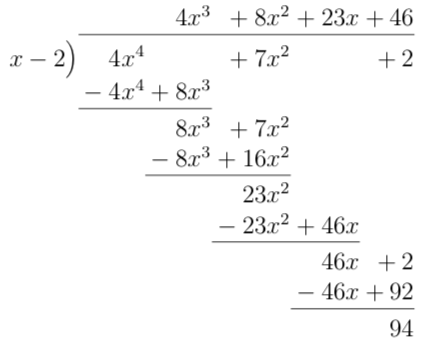
      Alltså \( \dfrac{4x^4+7x^2+2}{x-2} = 4x^3 + 8x^2 +23x +46 +\dfrac{94}{x-2} \).

    5. \( \dfrac{x^5+2x^3-1}{x^2+3} \)

      Vi får

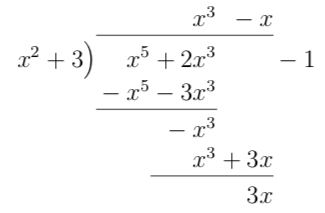
      Alltså \( \dfrac{x^5+2x^3-1}{x^2+3} = x^3 -x + \dfrac{3x-1}{x^2+3} \).

    6. \( \dfrac{x^4+x^3+4x-8}{x^2-x} \)

      Vi får

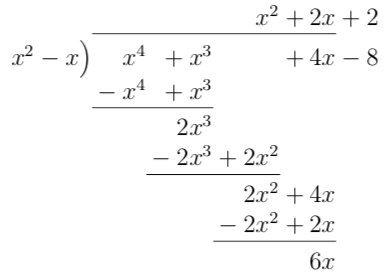
      Alltså \( \dfrac{x^4+x^3+4x-8}{x^2-x} = x^2+2x + \dfrac{6x-4}{x^2-x} \).

    7. \( \dfrac{x^3+x^2-6x}{x+1} \)

      Vi får

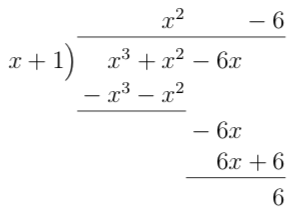
      Alltså \( \dfrac{x^3+x^2-6x}{x+1} = x^2 -6 + \dfrac{6}{x+1} \).

  2. Lös följande ekvationer.
    1. \( x^2 = 4x -5 \)

      Vi har \( x^2 - 4x +5 =0 \). Rotformeln ger \( x = 2 \pm i \).

    2. \( x^2 + x = -1 \)

      Vi har \( x^2 + x -1 =0 \). Rotformeln ger \( x = \dfrac{-1 \pm \sqrt{3}i}{2} \).

    3. \( 2x^2 - 10x = -13 \)

      Vi har \( 2x^2 -10x +13 = 0 \). Rotformeln ger \( x = \dfrac{5 \pm i}{2} \).

  3. Bestäm.
    1. \( (3 - 4i)+(2 +6i) \)

      Vi får \( (3 - 4i)+(2 +6i) = 5 + 2i \).

    2. \( (-2 -i)+(7 + i) \)

      Vi får \( (-2-i)+(7+i) = 5 \).

    3. \( (6 -3i)-(8-2i) \)

      Vi får \( (6-3i)-(8-2i) = -2-i \).

    4. \( -i-(7-2i) \)

      Vi får \( -i-(7-2i) = -7+i \).

  4. Bestäm.
    1. \( (3 - 4i)\cdot(2 +6i) \)

      Vi får \( (3 - 4i)\cdot(2 +6i) = 6+18i-8i-24i^2 = 30+10i \).

    2. \( (9 - 3i)\cdot(9 +3i) \)

      Vi får \( (9 - 3i)\cdot(9 +3i) = 81+27i-27i-9i^2 = 90 \).

    3. \( \dfrac{2-i}{3+2i} \)

      Kom ihåg att förlänga med konjugattalet.

      Vi får \( \dfrac{2-i}{3+2i} = \dfrac{4-7i}{13}\).

    4. \( \dfrac{3+4i}{3-4i} \)

      Kom ihåg att förlänga med konjugattalet.

      Vi får \( \dfrac{3+4i}{3-4i} = \dfrac{-7+24i}{25}\).

  5. Bestäm konstanten \( a \) så att divisionen \( \dfrac{3x^3-7x^2-ax-1}{3x-1} \) går jämt ut.

    Då \( a = -5 \). Se till att täljaren har samma nollställe som nämnaren.

  6. Bestäm konstanten \( a \) så att ekvationen \( 2x^4 + 5x^2 +a = 0 \) saknar lösning?

    Då \( a > 0 \).

    Undersök tecknen för \( 2x^4 \) och \( 5x^2 \). Minsta värdet för bägge är 0.

    Alltså gäller att \( a > 0 \).

  7. [SE H11] Isaac Newton lade år 1669 fram den metod för beräkning av funktioners nollställen som uppkallas efter honom. För att demonstrera metodens användbarhet använde han bland annat polynomet \( f(x)= x^3 -2x -5 \).
    1. Beräkna \( f'(x) \).

      \( f'(x) = 3x^2-2 \).

    2. Visa att den ekvation \( f(x)=0 \) som Newton undersökte har en lösning i intervallet \( [2,3] \).

      Eftersom \( f'(x) = 0 \) då \( \pm\dfrac{\sqrt{6}}{3} \approx \pm 0,82 \) är \( f \) strängt monotom i intervallet.

      Vi får att \( f(2) = -1 \) och \( f(3) = 16 \). Alltså har \( f \) exakt ett nollställe.

    3. Approximera lösningen genom att utföra fyra iterationer med Newtons metod. Använd begynnelsevärdet \( x_0=2 \). Ge svaret med fyra decimalers noggrannhet.

      Vi får

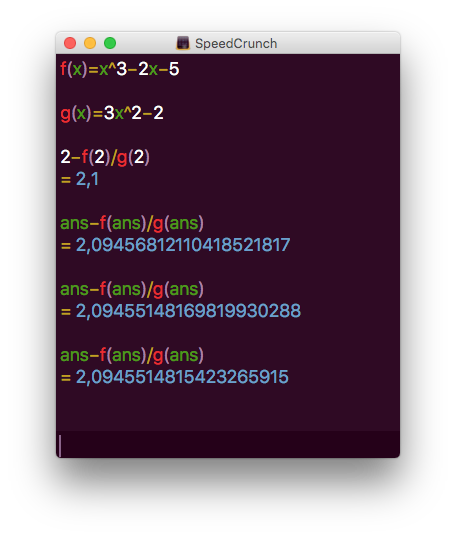
      Alltså 2,0946.

  8. [SE H14] Vi undersöker ekvationen \( x^5 - x = 1 \).
    1. Visa att ekvationen har exakt en lösning i intervallet \( 1 \leq x \leq 2 \).

      \( f'(x) = 5x^4-1 \). Derivatans nollställe är i \( x = \pm \dfrac{1}{\sqrt[4]{5}} \approx \pm 0,67 \). Derivatans nollställe är utanför intervallet. I intervallet \( 1 \leq x \leq 2 \) är \( f'(1) = 4 \), alltså är \( f \) växande.

      Eftersom \( f(1) = -1 \) och \( f(2)= 29 \). Betyder det att \( f \) skär \( x \)-axlen en gång.

      Alltså har ekvationen en lösing i intervallet \( 1 \leq x \leq 2 \).

    2. Bestäm genom att använda Newtons metod och startvärdet \( x_0 = 1 \) närmevärdet \( x_4 \) till lösningen i deluppgift a. Ange svaret med tre decimalers noggrannhet.

      Vi får

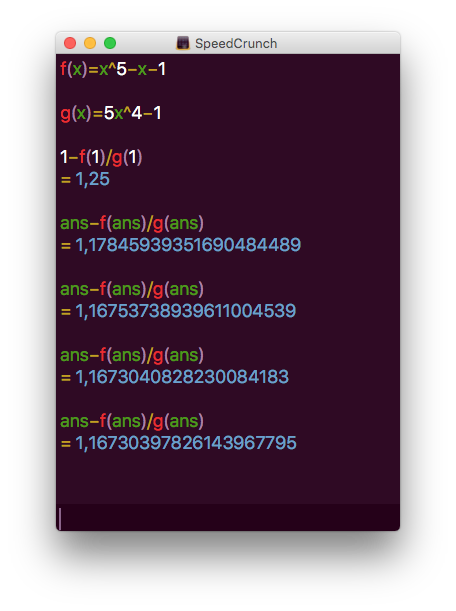
      Alltså 1,167.

  9. [SE V09] Bestäm med hjälp av Newtons metod en rot till ekvationen \( x^3 = x+2 \) med två decimalers noggrannhet. Visa att ekvationen har exakt en rot i intervallet \( [1,\infty[ \).

    Ekvationen \( x^3 = x + 2 \) är samma som \( f(x) = x^3 - x -2 = 0 \).

    Vi visar att \( f \) har ett nollställe och bestämmer nollstället.

    \( f'(x) = 3x^2-1 \). Derivatans nollställe är \( x = \pm \dfrac{\sqrt{3}}{3} \approx \pm 0,58 \). Eftersom vi jobbar i intervallet \( [1,\infty[ \) gäller att \( f'(1) = 2 \) och \( f \) är strängt växande.

    Då \( f(1) = -2 \) och \( f(2) = 4 \) betyder det att vi har ett nollställe i \( 1 \leq x \leq 2 \).

    Vi får

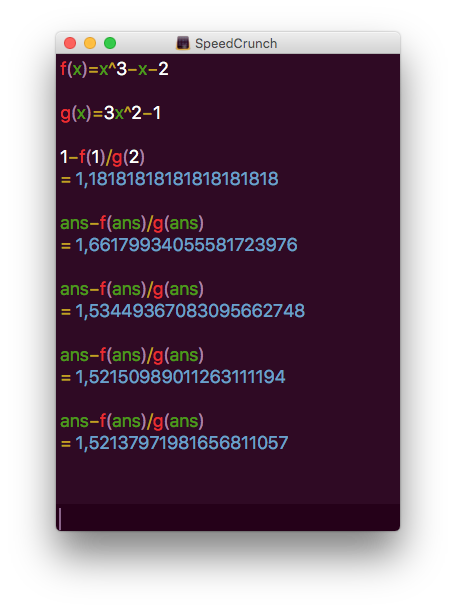
    Alltså 1,52.

  10. I början av året är saldot på ett konto 8 000 €. Pengar tas ut från kontot på ett sådant sätt att saldot minskar med 8 % varje år och i slutet av varje år görs en insättning om 200 €.
    1. Beskriv rekursivt en talföljd vars element \( x_n \) anger kontots saldo i början av \( n \):te året.

      Observera att vi har en minskning om 8 % och en ökning om 200 €.

      Vi får \[ \left \{ \begin{array}{ll} x_1 = 8000 \\ x_n = 0,92x_{n-1} + 200 & \text{då } n = 2,3,\ldots \\ \end{array} \right. \]

    2. Efter hur många år är saldot på kontot mindre än 4000 €?

      Gör det på LibreOffice.

      Kom fram till 17 år.

    3. Bilda ett uttryck \( x_n \) som vi kan beräkna talföljdens \( n \):te element med.

      Beteckna modigt elementen på ett allmänt sätt. Summan i början är \( a \), procentuella minskningen är \( q \) och summan som läggs till är \( b \).

      \( x_1 = a \)

      \( x_2 = qx_1 + b = qa + b \)

      \( x_3 = qx_2 + b = \ldots = q^2a +qb + b \)

      Fortsätt och märk att du har en geometrisk summa.

      Du kommer fram till \( x_n = q^{n-1}a + \dfrac{b(1-q^{n-1})}{1-q} \).

      Sätt in värden och förenkla. Kom fram till \( x_n = 0,92^{n-1}\cdot 5000+2500 \).

  11. [SE V21] Punkterna \( (x,y) \) i planmängden \( A \) bestäms av olikheterna \( 0 \le x \le 2 \), \( 0 \le y \le 4 \) och \( y \ge x^2 \). I den här uppgiften är målet att bedöma arean av mängden \( A \) med hjälp av en simulering genom att använda teorin att sannolikheten är direkt proportionell mot arean. Vi lottar fram punkter \( (x,y) \) ur rektangeln \( B \), som definieras av olikheterna \( 0\le x\le 2 \) och \( 0\le y\le 4 \).
    1. Gör med lämplig programvara en kod som lottar fram 1 000 punkter ur rektangeln \( B \) och som svar skriver ut antalet punkter som tillhör mängden \( A \). Beskriv i ord och med hjälp av lämpliga skärmdumpar hur du skapade din kod. (Ledtråd: Du kan exempelvis använda slumptalsgeneratorn i kalkylprogrammet.)

      (Sista parentesen är direkt från Studentprovet, du löser uppgiften i Python. (: Eller hur?)

      Följande är skrivet i replit.com

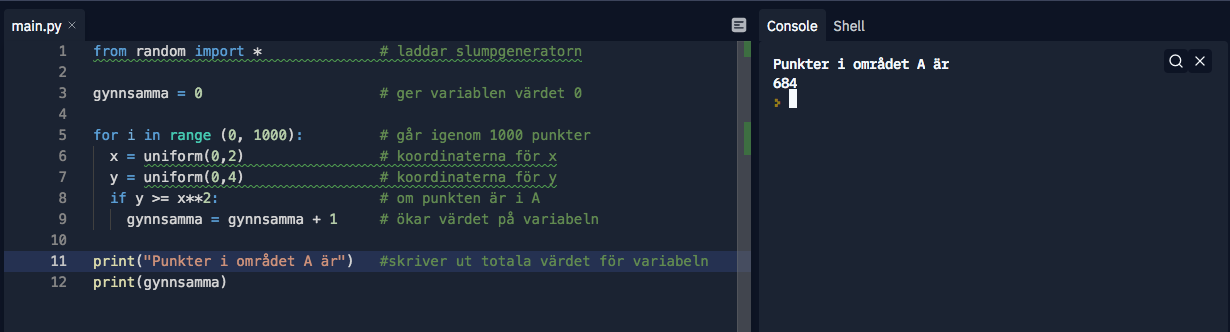
    2. Hillevi körde sin egen kod i deluppgift 1 tio gånger och fick talen nedan. Beräkna resultatens medelvärde och bedöm utifrån detta arean av mängden A.

      
Utskrifter av Hillevis kod: 673, 664, 672, 679, 667, 650, 640, 678, 660, 667

      Medeltalet är 665.

      Sannolikheten \( p = 0,665 \). Men sannolikheten är också \( p = \dfrac{A_A}{A_B} \) där \( A_A \) och \( A_B \) är areorna för mängderna.

      Vi får ekvationen \( 0,665 = \dfrac{A_A}{A_B} \). Vi vet att \( A_B = 2 \cdot 4 = 8 \).

      Vi får alltså \( 0,665 = \dfrac{A_A}{8} \) och \( A_A = 5,32 \).

  12. [SE V20] Det geometriska medelvärdet av två positiva tal \( a \) och \( b \) är \( \sqrt{ab} \).
    1. Ge exempel på två olika heltal \( a \) och \( b \) , där vardera talet ligger i intervallet 2–100 och för vilka \( \sqrt{ab} \) är ett heltal. (3 p.)

      Exempel: a = 2 och b = 8, vilket ger \( \sqrt{ab} = 4 \).

    2. En slumptalsgenerator lottar ut två heltal i intervallet 1–100 oberoende av varandra och så att varje tal väljs med sannolikheten \( \dfrac{1}{100} \). Vilken är sannolikheten för att det geometriska medelvärdet av talen är ett heltal? Du kan beräkna händelsens klassiska sannolikhet exakt eller ge en uppskattning av sannolikheten med stöd av en simulering. (9 p.)

      (Gör simuleringen på Python.)

      Lösningen

  13. Skapa ett program som löser följande uppgift:

    Vi söker ögontal för tre tärningar.

    Om du adderar ögontalet är svaret 6.

    Inga ögontal intill varandra har samma ögontal.

    Om du multiplicerar ögonen är svaret 4.

    Utmana dig själv så att värdet för summan och multiplikationen väljs slumpmässigt och programmet klarar av att hitta ögontalen.

    Lösningen

  14. Skriv ett program som utnyttjar Newtons metod som kan bestämma närmevärden med 6 decimalers noggrannhet för kvadratrötter.

    Lösningen