5. Iteration och rekursivt definierad talföljd
Vi börjar med att undersöka von Kochs kurva.
VideoExempel 1 Låt \( f(x)=2x-1\). Iterera funktionen
- med startvärdet 1,
- med startvärdet \( x \).
I MaG arbetade vi med talföljder. Då tittade vi på talföljder där följande element är beroende av föregeående element. Dessa talföljder kallas för rekursivt definierade talföljder.
Rekursivt definierad talföljd
Vi studerar talföljden där \(a_1=4\) och \(a_n= \dfrac{1}{a_{n-1}}+n, n=1,2,3,\ldots\).
Talföljder där nästa element baserar sig på föregående element heter rekursiva talföljder.
Exempel 2 Bestäm de 5 första elementen för talföljden \(a_1 = 2\), \(a_n=a_{n-1}-2n\) då \(n=1,2,3\ldots\).
Lösning
Vi bygger upp följande talföljd:
\(a_1 = 2\)
\(a_2 = a_1 -2 n = 2 -2\cdot 2 = -2\)
\(a_3 = a_2 -2 n = -2 -2\cdot 3 = -8\)
\(a_4 = a_3-2n = -8-2\cdot 4 = -20\)
\(a_5 = a_4-2n= -20 -2\cdot 5 = -30\)
Exempel 3 Bestäm den allmänna formen för följande rekursivt definierade talföljder.
- \(a_1=3\), \(a_n=3a_{n-1}\) då \(n=2,3,4,\ldots\)
- \(a_1=1\), \(a_n=(1-\dfrac{1}{n})a_{n-1}\) då \(n=2,3,4,\ldots\).
Lösning
Vi har
\(a_1=3\)
\(a_2=3 \cdot 3 = 3^2\)
\(a_3=3 \cdot 3^2=3^2\)
\(a_n=3^n\).
\(a_1 = 1\)
\(a_2 = (1-\dfrac{1}{2})1 = \dfrac{1}{2}\)
\(a_3 = (1-\dfrac{1}{3})\dfrac{1}{2} = \dfrac{2}{3}\cdot\dfrac{1}{2} = \dfrac{1}{3}\)
\(a_4 = (1-\dfrac{1}{4})\dfrac{1}{3} = \dfrac{3}{4}\cdot\dfrac{1}{3} = \dfrac{1}{4}\)
\(a_n= \dfrac{1}{n}, n=1,2,3,\ldots\).
För att exakt visa att den allmänna formen ger exakt samma talföljd som den rekursivt definierade använder man sig av matematisk induktion. I kurs 11 tränar vi oss på det.
Exempel 4 Bestäm de första termerna i talföljden som bestäms som \(a_n=a_{n-1}+a_{n-2}\).
Lösning
\(a_3 = a_2+a_1\)
\(a_4 = a_3+a_2 = (a_2+a_1) + a_2 = 2a_2+a_1\)
\(a_5 = a_4+a_3 = (2a_2+a_1) + (a_2+a_1) = 3a_2+2a_1\)
\(a_6 = a_5+a_4 = (3a_2+2a_1) + (2a_2+a_1) = 5a_2+3a_1\)
\(a_7 = a_6+a_5 = (5a_2+3a_1) + (3a_2+2a_1) = 8a_2 +5a_1\).
Vi märker att alla termer är uppbyggda och beroende av \(a_1\) och \(a_2\).
Exempel 5 För en insektpopulation på 10 000 individer gäller att varje år ökar populationen med 9 % och efter årets ungar är uppfödda flyttar 500 st insekter ut för att bilda en ny population.
- Bilda den rekursiva talföljden.
- Efter hur många år överskrider populationen 15 000 insekter?
Lösning
Vi får
\(\begin{array}{cl} År & \text{Antal, lämpligt avrundat vid behov} \\ 1 & 10000 \\ 2 & 10000 \cdot 1,09 -500 = 10400 \\ 3 & 10400 \cdot 1,09 -500 = 10836 \\ 4 & 10836 \cdot 1,09 -500 = 11311 \\ 5 & 11829 \\ 6 & 12394 \\ 7 & 13009 \\ 8 & 13680 \\ 9 & 14411 \\ 10& 15208 \\ \end{array}\)
Efter 10 år överskrider populationen 15 000 individer.
Om vi gör det exakt får vi
\(\begin{array}{cl} År & \text{Exakt} \\ 1 & 10000 \\ 2 & 10000\cdot1,09-500 \\ 3 & (10000\cdot 1,09 - 500)1,09-500 = 10000\cdot1,09^2-500\cdot1,09 -500 \\ 4 & (10000\cdot1,09^2-500\cdot1,09 -500)1,09-500 \\ & =10000\cdot1,09^3-500\cdot1,09^2- 500\cdot1,09 -500 \\ n & 10000\cdot1,09^{n-1} -500\cdot1,09^{n-2} -500\cdot1,09^{n-3} -\ldots-500\cdot1,09^1 -500 \\ \end{array}\)
Den andra delen är en geometrisk summa där \(a_1=500\) och \(q=1,09\). Summan av den är \(\dfrac{-500(1-1,09^{n-1})}{1-1,09}\).
Vi får att \(10 000\cdot 1,09^{n-1} +\dfrac{-500(1-1,09^{n-1})}{1-1,09} > 15 000\) som har lösningen \(n>9,75\). Alltså 10 år.
Rekursivt definieradet talföljder på LibreOfficeCalc
Uppgifter
- Waclaw Sierpinksi var en polsk matematiker som undersökte mängdlära, talteori, funktioner och topolgi. Han skapade två figurer som bygger på fraktaler, Sierpinski triangeln och Sierpinski mattan.
- Sierpinski trianglen skapar vi på följande sätt.
- Rita en triangel.
- Förena mittpunkterna till triangelns sidor så att det bildas en mindre triangel. Färglägg den mindre triangeln.
- I figuren bildas nya vita trianglar. Upprepa steg 2 för varje vit triangel upprepande gånger.
Vi får något i stil med

Om vi fortsätter får vi

- Sierpinski mattan skapar vi på följande sätt.
- Rita en kvadrat.
- Dela kvadraten i 9 mindre lika stora kvadrater och färglägg den mittersta kvaraten.
- I figuren bildas vita kvadrater. Upprepa steg 2 för varje vit kvadrat upprepande gånger.
Vi får något i stil med






- Sierpinski trianglen skapar vi på följande sätt.
- Sumererna kunde redan för 4 000 år sedan bestämma ett närmevärde för talet \( \sqrt{a} \) med hjälp av följande algortim:
- Börja med en kvalificerad gissning, \( b > 0\).
- Nästa värde får vi genom att räkna medelvärdet av \( b \) och \( \dfrac{a}{b} \).
- Vi fortsätter på samma sätt upprepande gånger.
- Använd algoritmen för att bestämma ett närmevärde för \( \sqrt{3} \).
Vi gissar på \( 1 \) eftersom \( 1 < 3 < 2^2 \).
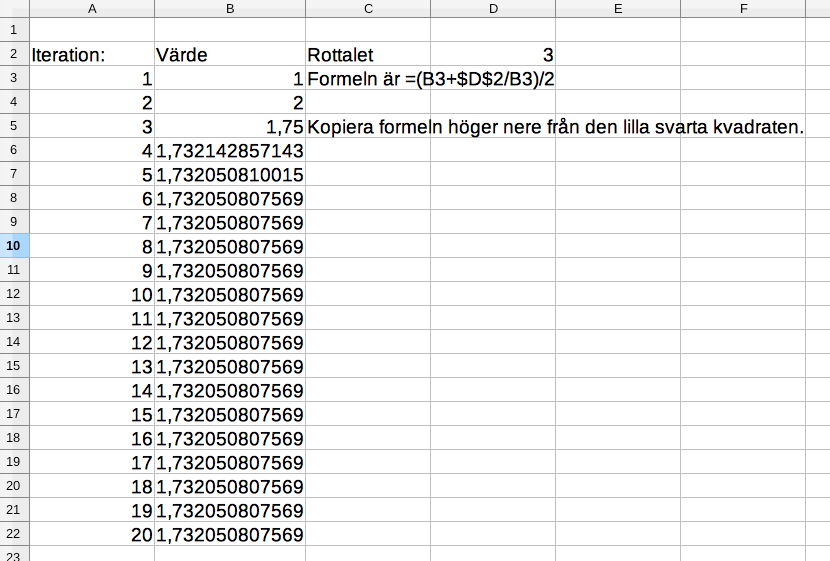
Vi kommer att närma oss \( 1,73205\ldots \).
- Använd algoritmen för att bestämma ett närmevärde för \( \sqrt{17} \).
Vi gissar på \( 4 \) eftersom \( 4^2 < 17 < 5^2 \).
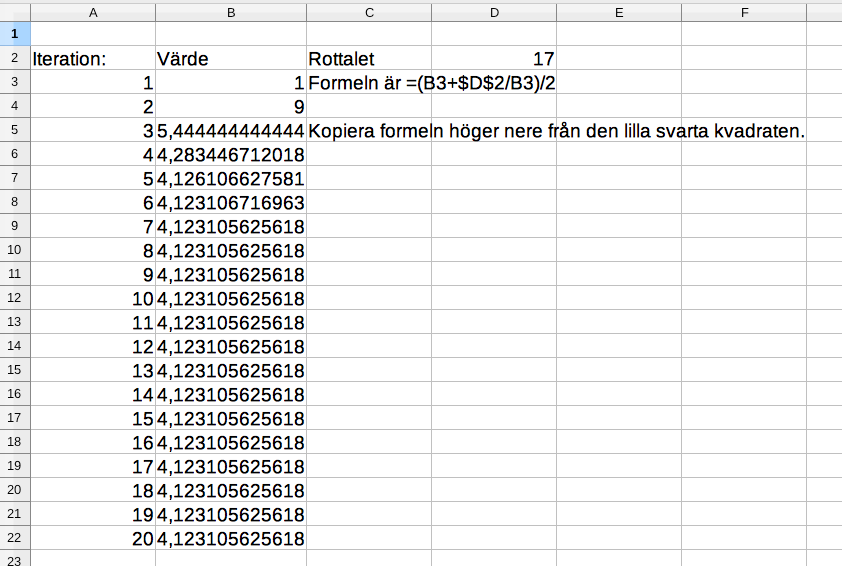
Vi kommer att närma oss \( 1,73050\ldots \).
- Beskriv algoritmen som en rekursiv talföljd.
Lösningen
- Iterera funktionen \( f(x) = 1 + \dfrac{1}{x^2} \) med startvärdet 1. Vilket tal kommer vi att närma oss?
Vi får
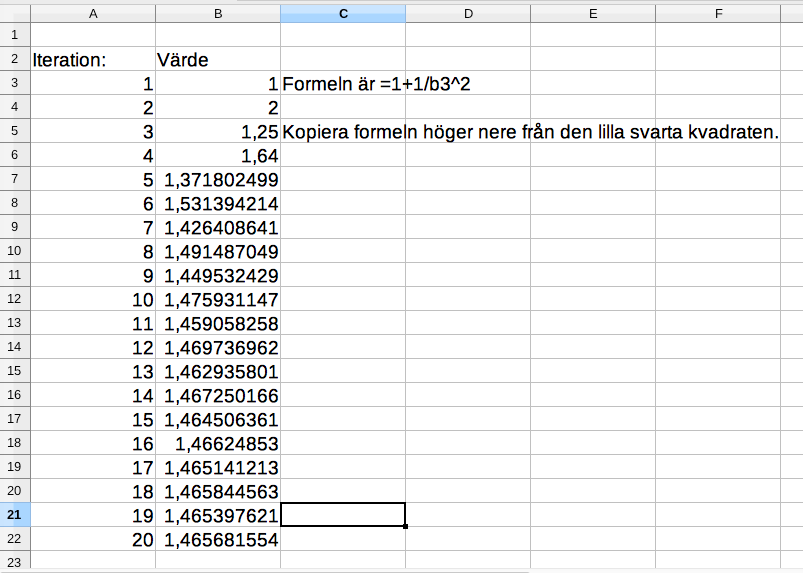
Vi kommer att närma oss 1,465.
- Iterera funktionen \( f(x) = 3x - 2 \) med startvärdet \( x \). Bestäm resultatet av de fem första iterationerna.
Vi får
\( \begin{array}{rcl} f^1(x) & = & 3x -2 \\ f^2(x) & = & 3(3x-2)-2 = 3^2x-3\cdot 2-2 \\ f^3(x) & = & 3(3^2x-3\cdot 2-2) - 2 = 3^3x-3^2\cdot 2 - 3\cdot 2 - 2 \\ f^4(x) & = & 3(3^3x-3^2\cdot 2 - 3 \cdot 2 - 2) -2 = 3^4 x - 3^3 \cdot 2 - 3^2 \cdot 2 -3\cdot 2 - 2 \\ f^5(x) & = & 3(3^4 x - 3^3 \cdot 2 - 3^2 \cdot 2 -3\cdot 2 - 2) -2 = 3^5 x - 3^4 \cdot 2 - 3^3 \cdot 2 - 3^2 \cdot 2- 3\cdot 2 - 2 \\ \end{array} \)
- Iterera funktionen \( f(x) = x + 3 \) med startvärdet \( x \). Bestäm värdet efter den \( n\):te iterationen \( f^n(x) \).
Vi får
\( \begin{array}{rcl} f^1(x) & = & x+3 \\ f^2(x) & = & x+3 + 3 = x + 2 \cdot 3 \\ f^3(x) & = & x + 2 \cdot 3 + 3 = x+ 3 \cdot 3 \\ f^4(x) & = & x+ 3 \cdot 3 + 3 = x+ 4 \cdot 3 \\ f^n(x) & = & x+ n \cdot 3 \\ \end{array} \)
- Bestäm de tre följande elementen för talföljden \(a_n=2-na_{n-1}\) då \(a_1=3\) och \(n=2,3,\ldots\).
\( a_1 = 3, a_2 = -4, a_3 = 14 \) och \( a_4 = -54 \).
- Bestäm de fyra följande elementen för talföljden som börjar med \(a_1=2\) och som bestäms rekursivt av \(a_n=3-a_{n-1}\).
\( a_1 = 2, a_2 = 1, a_3 = 2, a_4 = 1 \) och \( a_5 = 2 \).
- Bestäm de fyra följande elementen för den rekursiva talföljden som defineras som \(a_n = a_{n-1} +2a_{n-2}\) då \(a_1 = 2\) och \(a_2=4\).
\( a_1 = 2, a_2 = 4, a_3 = 8, a_4 = 16, a_5 = 32 \) och \( a_6 = 64 \).
- Bestäm den allmänna formeln för följande rekursivt definierade talföljder
- \(a_1 = 2\), \(a_n=a_{n-1}+2\) då \(n=2,3,4,\ldots\)
\(a_1 = 2\)
\(a_2 = 2 + 2 = 4\)
\(a_3 = 4 + 2 = 6\)
\(a_4 = 6 + 2 = 8\)
\(a_n = 2n, n=1,2,3\ldots\)
- \(a_1 =1\) och \(a_n=2a_{n-1}\) då \(n=2,3,4,\ldots\)
\(a_1 = 1\)
\(a_2 = 2\cdot 1 = 2\)
\(a_3 = 2\cdot 2 = 4\)
\(a_4 = 2\cdot 4 = 8\)
\(a_5 = 2\cdot 8 = 16\)
\(a_n = 2^{n-1}, n=1,2,3,\ldots\)
- \(a_1 = 1\) och \(a_n=na_{n-1}\), då \(n=2,3,4,\ldots\)
\(a_1 = 1\)
\(a_2 = 2\cdot 1 = 2\)
\(a_3 = 3\cdot 2 = 6 = 3\cdot 2\cdot 1 \)
\(a_4 = 4\cdot 6 = 24 = 4\cdot 3\cdot 2\cdot 1 \)
\(a_n = n!, n=1,2,3,\ldots\)
- \(a_1 = 2\), \(a_n=a_{n-1}+2\) då \(n=2,3,4,\ldots\)
- Bestäm den allmänna formeln för följande rekursivt definierade talföljder.
- \(a_1= 1\) och \(a_n=\dfrac{a_{n-1}}{2}\) då \(n=2,3,4,\ldots\)
\(a_1 = 1\)
\(a_2 = \dfrac{1}{2}\)
\(a_3 = \dfrac{\frac{1}{2}}{2} = \dfrac{1}{4}\)
\(a_4 = \dfrac{\frac{1}{4}}{2} = \dfrac{1}{8}\)
\(a_5 = \dfrac{\frac{1}{8}}{2} = \dfrac{1}{16}\)
\(a_n= \dfrac{1}{2^{n-1}}, n=1,2,3,\ldots\).
- \(a_1= 3\) och \(a_n=\dfrac{a_{n-1}}{n}\) då \(n=2,3,4,\ldots\)
\(a_1 = 3\)
\(a_2 = \dfrac{3}{2}\)
\(a_3 = \dfrac{\frac{3}{2}}{3} = \dfrac{3}{6}\)
\(a_4 = \dfrac{\frac{3}{6}}{4} = \dfrac{3}{24}\)
\(a_n = \dfrac{3}{n!}, n=1,2,3,\ldots\)
- \(a_1= 1\) och \(a_n=\dfrac{a_{n-1}}{2}\) då \(n=2,3,4,\ldots\)
- I en stad bor det 25 000 personer. Varje år föds det 1,5 % nya invånare och pga av missnöje flyttar det varje bort 200 personer.
- Bilda den rekursiva talföljd som beskriver mängden invånare i staden.
\(a_1 = 25000\)
\(a_n = a_1 \cdot 1,015-200\)
- Efter hur många år överstiger befolkningen 26 000 invånare?
En tabell med värden ger 7 år.
- Bilda den rekursiva talföljd som beskriver mängden invånare i staden.
- En talföljd definieras som \(a_1=4\) och \(a_{n+1}=a_n+k\). För vilket värde på \(k\) gäller att \(\sum_{i=1}^5 a_i = 0\)?
Vi får
\(\begin{array}{rcl} \sum_{i=1}^5 a_i &=& 0 \\ 4 + [4+k] + [(4+k)+k] + [(4+k+k)+k] + [(4+k+k+k)+k] &=& 0 \\ 5\cdot 4 + 10k &=& 0 \\ 10k &=& -20 \\ k &=& -\frac{10}{20} = -\frac{1}{2}\\ \end{array}\)
- En del av kursen är att lära sig programmera. Gå till tie.koodariksi.fi, registrera dig och börja jobba på Ohjelmoinnin alkeet. Uppe till höger kan du byta språk.
Jobba ca en timme med materialet, eller med kapitlen 13-14.