1. Primitiv funktion
Visa att \( f(x)= 2x+4 \) är derivatafunktion för \( F(x)=(x+2)^2 \).
Lösning
\( F(x)=(x+2)^2=x^2+4x+4 \). Derivatafunkitionen är \( F'(x)=2x+4 =f(x) \).
Exempel 1 Bestäm andra funktioner vars derivatafunktion är \( f(x)=2x+4 \).
De funktioner som uppfyller villkoret \( f(x)=F'(x) \) är de primitiva funktionerna, \( F(x) \), för funktionen \( f(x) \). Funktionen \( f(x) \) har oändligt många primitiva funktioner.
Exempel 2 Bestäm alla primitiva funktioner för \( f(x)= 6x^2-4x \).
Lösning
En primitiv funktion för \( f(x) \) är \( F(x)=2x^3-2x^2 \). Vi kan addera till en konstant eftersom derivatan av en konstant har värdet noll.
Alla primitiva funktioner är \( F(x)=2x^3-2x^2+C \).
En primitiv funktion för \( f(x) \) är \( F(x) \) där \( F'(x)=f(x) \). Alla primitiva funktioner får vi genom att addera till en konstant, \( C \). Alla primitiva funktioner för \( f(x) \) är \( F(x)+C \).
Exempel 3 Bestäm den primitiva funktion för \( f(x)=\sin x \) som går genom punkten \( (0,1) \) .
Lösning
\( F(x)=-\cos x + C \) eftersom \( F'(x)=\sin x \). Då \( F(x) \) skall gå genom punkten \( (0,1) \) betyder det att \( F(0) = 1 \), alltså \( -\cos 0 + C = 1 \Leftrightarrow C=2 \).
Den sökta primitiva funktionen är \( F(x)=-\cos x +2 \).
Uppgifter
Välj de primitiva funktionerna för \( f(x)=4x^3 -4x \) och \( g(x)=3x^2+1 \).
Påstående \( f(x)=4x^3 -4x \) \( g(x)=3x^2+1 \) Varken \( f(x) \) eller \( g(x) \). \( h(x)= x^4-2x^2 +2 \) \( i(x)= x^4-2x^2 -1 \) \( j(x)= 12x^2-4 \) \( k(x)= x^4-2x^2 \) \( l(x)= x^3+x+2 \) \( m(x)= x^3-x \) \( n(x)= x^3+x \) \( o(x)= 6x \) \( p(x)= x^3+x-1 \) \( q(x)= 4x^3-4x \) Påstående \( f(x)=4x^3 -4x \) \( g(x)=3x^2+1 \) Varken \( f(x) \) eller \( g(x) \). \( h(x)= x^4-2x^2 +2 \) \( i(x)= x^4-2x^2 -1 \) \( j(x)= 12x^2-4 \) \( k(x)= x^4-2x^2 \) \( l(x)= x^3+x+2 \) \( m(x)= x^3-x \) \( n(x)= x^3+x \) \( o(x)= 6x \) \( p(x)= x^3+x-1 \) \( q(x)= 4x^3-4x \) - Bestäm alla primitiva funktioner för följande funktioner
- \( f(x)=6x-2 \)
\( F(x)=3x^2-2x + C \) eftersom \( F'(x)=6x-2 \).
- \( f(x)=e^x \).
\( F(x)=e^x + C \) eftersom \( F'(x)=e^x \).
- \( f(x)=\dfrac{3}{x^2} \)
\( F(x)= -\dfrac{3}{x}+C \) eftersom \( F'(x)=D(-3x^{-1}+C)=3\cdot x^{-2} \).
- \( f(x)=6x-2 \)
- Bestäm alla primitiva funktioner för
- \( f(x)=3x^2+8x \)
\( F(x)=x^3+4x^2 + C \) eftersom \( F'(x)=3x^2+8x \).
- \( g(x)= \sin x \).
\( G(x)=-\cos x + C \) eftersom \( G'(x)=\sin x \).
- \( h(x)= 3^x \ln 3\)
\( H(x)= 3^x+C \) eftersom \( H'(x)= 3^x \ln 3 \).
- \( f(x)=3x^2+8x \)
- Kombinera rätt primitiv funktion med rätt funktion.
Välj bland följande primitiva funktioner
så att de får rätt funktion.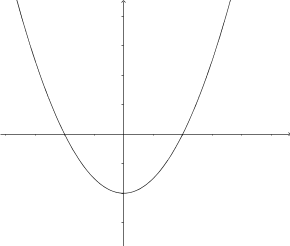
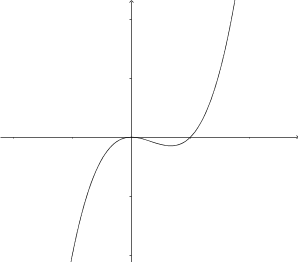
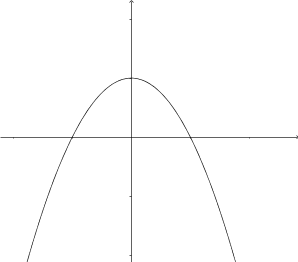
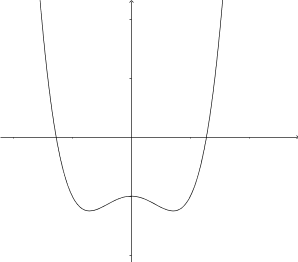
Primitiv funktion Funktion 
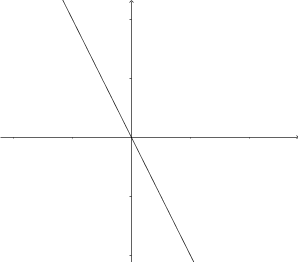
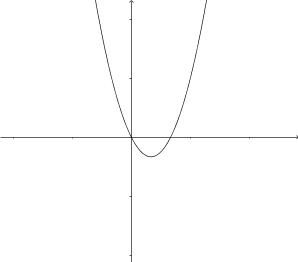

Primitiv funktion Funktion 







- Visa att \( F(x)=\dfrac{1}{x} \) är en primitiv funktion för funktionen \( f(x)=-\dfrac{1}{x^2} \).
\( F(x)=\dfrac{1}{x} = x^{-1} \). \( F'(x)=-x^{-2}=-\dfrac{1}{x^2} =f(x) \).
- Visa att \( F(x)=x\ln(x)-x \) är en primitiv funktion för funktionen \( f(x)=\ln x \).
\( F'(x)=D(x\ln x - x)=1\ln x + x\cdot \dfrac{1}{x}-1 = \ln x +1-1 = \ln x \).
- Visa att \( F(x)=\dfrac{1}{2}\cos^2 x \) är en primitiv funktion för funktionen \( f(x)=-\sin(x)\cos(x) \).
\( F'(x)=D(\dfrac{1}{2}\cos^2 x) = \dfrac{1}{2}\cdot2\cos x D(\cos x)=\cos x (-\sin x)=-\sin x \cos x \).
- Bestäm den primitiva funktion för \( f(x)=3x^2-8x \) som går genom punkten (1,-1).
\( F(x)=x^3-4x^2+C \) eftersom \( F'(x)=f(x) \). \( F(1)=-1 \) ger oss \( 1^3-4\cdot1^2+C=-1 \Leftrightarrow C = 2 \).
Alltså \( F(x)=x^3-4x^2+2 \).
- Bestäm den primitiva funktion för \( f(x)=\dfrac{-2}{(x-1)^2} \) som går genom punkten (2,2).
\( F(x)=\dfrac{2}{x-1} + C \) eftersom \( F'(x)=\dfrac{(x-1)D2-2D(x-1)}{(x-1)^2} = \dfrac{-2}{(x-1)^2} \).Att \( F(2)=2 \) ger oss \( \dfrac{2}{2-1}+C=2 \Leftrightarrow C=0 \).
Alltså \( F(x)=\dfrac{2}{x-1} \).
- Bestäm för funktionen \( f(x) = 3x^2+1 \) de primitiva funktioner som tangerar linjen \( y = 4x +1 \).
Primitiva funktionerna är av typ \( F(x)= x^3 + x + C \). Eftersom \( f(x) \) är derivatafunktion för \( F(x) \) och lutningen för tangenten är 4 får vi att \( f(x)=4 \), alltså \( 4=3x^2+1 \) ger \( x = \pm 1 \).
Då \( x = 1 \) gäller att \( F(1) = 5 \), alltså \( 1^3 + 1 + C = 5 \) ger \( C = 3 \) och då \( x = -1 \) gäller att \( F(-1) = -3 \), alltså \( (-1)^3+(-1)+C = -3 \) ger \( C = -1 \).
De primitiva funktionerna är \( F(x) = x^3 +x + 3 \) och \( F(x) = x^3 +x -1 \).
- Visa att alla primitiva funktioner för funktionen \( f(x) = \sin^4 x \) är växande för alla reella tal.
För den primitiva funktionen \( F \) gäller att \( F'(x) = f(x) \).
Eftersom \( f(x) \) är positiv och får värdet noll i \( n \pi \) där \( n \) är ett heltal, gäller det att \( F(x) \) är växande.
- Fundera på följande tillsammans med en kurskamrat.
- Är det lätt att ställa en fråga? Varför?
- Är det lätt att ställa en bra fråga? Varför?
- Är det lätt att ställa en bra matematisk fråga? Varför?
- Finns det inom matematiken bättre och mindre bättre bra frågor?
- Vad är förutsättningen för en bra matematisk fråga?
- Vad är viktigare inom matematiken: att ställa en bra fråga, eller att svara bra? Förklare lite.
- Vem ställer frågor under en matematiklektion? Läraren? De studerande som snabbt förstår? De studerande som långsamt förstår?
- Kan man i grupp formulera en bra fråga eller måste man göra det individuellt? Förklara.
Källa: Filosofoidaan matematiikasta ja luonnontieteistä; Daniel, Lafourtune, Pallascio, Sykes