9. Tillämpningar

Grattis! Då har du egentligen kommit så långt att allt efter detta är bara tillämpning av det som du hittills har lärt dig. Vi fortsätter med att se på tillämpningar.

Exempel 1 De flesta flygbolag tillämpar för handbagaget 115 cm regeln som betyder att summan av längden, bredden och höjden maximalt 115 cm. Bestäm största möjliga volym för en resväska som är dubbelt så lång som bred.

Exempel 2 Då en butikschef sänker priset på en vara med p % ökar försäljningen 1,4p. Med hur många procent skall butikschef sänka priset för att vinsten skall vara så stor som möjligt?

Exempel 3 Golden Gate bron är en så kallad hängbro. Det betyder att den hänger med hjälp av vajrar som är fästa vid pelare, se bild.

Hur stor vinkel bildar vajern med markplanet vid pelarna?

Bilden hittar du här.

För att anpassa en funktion genom punkter arbetar vi med FitPoly-kommandot.

Exempel 4 En talföljd defineras som \( a_n = \dfrac{1}{n^2+1}, n \in \mathbb{N} \). Visa att talföljden är strängt avtagande.

I funktionen ovan har vi något som är en sammansatt funktion. Hur vi deriverar sammansatta funktioner kommer i kurs 7. Exemplet och videon är från gamla läroplanen och skall hitta en ny plats. Tanken att visa att en talföljd är monotom gäller dock.

För att bestämma punkter där vi har största eller minsta förändringar undersöker vi andra derivatan, \( f'' \). Det betyder att vi deriverar derivatafunktionen \( f' \).

Uppgifter

En butikschef som säljer jeans märker att för varje 5 € som hen höjer priset så säljer hen 10 par mindre jeans per vecka. Hur mycket skall hen ändra på priset för att maximera sina intäkter då hen nu säljer jeans för 75 € styck och då går det åt 80 par i veckan? Vad blir hens intäkter efter prisjusteringen?

Vi bildar en tabell före vi bilar funktionen.

	Nu	Sedan
Pris	75 €	75 + 5n
Volym	80 st	80 - 10n
Intäkter	\( 75 \cdot 80 \)	\( (75+5n)(80-10n) \)

Funktionen är \( f(n)=-50n^2-350n+6000 \).

\( f'(n)=-100n -350 \). Vi har \( f'(n)=0 \) då \( n=-3,5 \).

Det nya priset på jeansen är 57,50 € och Butikschefens nya intäkter är 6612,50 €.

Från ett A4 ark (210 x 297 mm) klipper man bort kvadrater i varje hörn och viker upp sidorna så att vi får en ask. Hur stora kvadrater skall vi klippa bort då vi vill ha så stor volym på asken som möjligt?

Funktionen som ger volymen är \( V(x)=(210-2x)(297-2x)x = 4x^3-1014x^2+62370x \). Intervallet är \( ]0,105[ \) som kommer från \( 210-2x > 0 \) och att vi behöver en höjd, \( x > 0 \).

\( V'(x)=12x^2-2028x+62370 \) och \( V'(x)=0 \) ger \( x=40,42 \) och \( x=128,58 \), som är utanför intervallet.

\( V(0)=4\cdot 0^3=1014\cdot 0^2 +62370\cdot 0 =0 \)

\( V(40,42) = 4\cdot 40,42^3=1014\cdot 40,42^2 +62370\cdot 40,42 =1128400 \)

\( V(105)= 4\cdot 105^3=1014\cdot 105^2 +62370\cdot 105 =0 \)

Största volym får vi då vi klipper bort sidor om 40,4 mm.
För ett akvarie finns det 8,0 m metallist för att bygga kanterna av. Bestäm dimensionerna för det akvarie där sidoytorna är formade som kvadrater och som har maximal volym.

Vi betecknar längden med \( a \) och sidoytorna med \( b \). För längden gäller att \( 4a+8b=8 \).

Funktionen som ger volymen är \( V(b)=b^2 a=b^2(2-2b) \).Intervallet som vi undersöker i är \( ]0,1[ \). \( V'(b)=-6b^2+4b \) som har nollställena \( b=0 \) och \( b=\dfrac{2}{3} \). Då vi jämför värdena i derivatans nollställen och intervallets ändpunkter märker vi att akvariets längd, bredd och höjd skall vara 66,6 cm.
För ett rektangelformat område finns det staket för 60 m. Bestäm dimensionerna, längd och bredd, för området då man vill att arean är så stor som möjligt.

Vi betecknar längden med \( l \) och bredden med \( b \).

Arean för området är \( A = lb \). För omkretsen gäller \( 2l+2b = 60 \), alltså \( b = 30 - l \).

Vi bildar en funktion som ger arean, \( A (l) = l(30-l) = -l^2 +30l \), där \( 0 < l < 30 \).

Vi får \( A'(l) = -2l+30 \).

Derivatans nollställe, \( -2l + 30 = 0 \) ger \( l = 15 \).

Funktionens extremvärden hittar vi i derivatans nollställen eller i intervallet ändpunkter.

\( A(0) = 0 \) m².

\( A(15) = 225 \) m².

\( A(30) = 0 \) m².

Alltså skall längden vara 15 m och bredden 15 m.
En köpman värderar att om hen höjer priset för T-skjortor med 1 € så säljer hen 5 st färre per vecka. Då en T-skjorta kostade 30 € sålde hen 100 st skjortor per vecka. Vilket pris borde köpmannen be per T-skjorta för att maximera vinsten? Hur stor är värdet av försäljningen då?

Vi får nya priset till \( 30 + x \).

Den nya mängden T-skjortor som säljs är \( 100 - 5x \).

Då får vi funktionen som ger värdet av totala försäljningen \( f(x) = (100-5x)(30+x) \).

Eftersom priset inte kan vara negativt får vi \( 30 + x \geq 0 \), alltså \( x \geq -30 \).

Antalet skjortor som säljs kan inte vara negativt, \( 100 - 5x \geq 0 \), alltså \( x \leq 20 \).

Förenkla och derivera funktionen. Kom fram till att \( f'(x)=0 \) då \( x=-5 \).

Sök största värde i intervallets endpunkter och i derivatans nollställe.

Kom fram till att priset skall sänkas med 5 €, priset per skjorta är 25 € och värdet av försäljningen är 3 125 €.
Två hörn av en rektangel är på parabeln \( f(x)=-x^2+4 \) och två på \( x \)-axeln. Bestäm arean av den största rektangel som ryms in under parabeln.

Längden är \( 2x \) och höjden är \( -x^2+4 \). Intervallet som duger är \( ]0,2[ \).

Areafunktionen är \( A(x)=2x(-x^2+4)=-2x^3+8x \) i \( ]0,2[ \).

\( A'(x)=-6x^2+8 \) som har nollställena \( x=\sqrt{\dfrac{4}{3}}=\dfrac{2}{\sqrt{3}} \approx 1,15 \).

Största arean hittar vi i derivatans nollställe eller i intervallets ändpunkter.

\( A(0)=-2\cdot0^3+8\cdot0 =0 \)

\( A(\dfrac{2}{\sqrt{3}})=-2\cdot(\dfrac{2}{\sqrt{3}})^3+8\cdot\dfrac{2}{\sqrt{3}} =\dfrac{32}{3\sqrt{3}} \)

\( A(2)=-2\cdot2^3+8\cdot2 =0 \)

Största värdet är \( \dfrac{32}{3\sqrt{3}}\approx 6,2 \).

Då man ökar på tryckhastigheten för en tryckmaskin ökar stoppen i produktionen. Då manskinen är inställd på att trycka 5 000 ark i timmen, fungerar den 20 timmar i dygnet. Man värderar att för varje ökning på 100 tryckta ark ökar på tiden på stoppen med 15 min. Vilken hastighet borde tryckmaskinen vara inställd på så att antalet ark som trycks per dygn är så stort som möjligt? Hur många ark trycker maskinen per dygn då?

Vi bildar en funktion som anger totala mänden tryckta papper per dygn.

Hastighet, ark/timme	tid i drift
5 000	20
\( 5000 + 400 = 5 400 \)	\( 20 - 4 \cdot 0,25 \)
\( 5000 + t\cdot 100 \)	\( 20 - t \cdot 0,25 \)

Funktionen är \( f(t) = (5000+100t)(20-0,25t) = -25t^2+750t+100000 \).

Derivatafunktionen är \( f'(t) = -50t+750 \).

Derivatans nollställe \( f'(t) = 0 \) då \( t = 15 \).

Eftersom funktionen \( f \) är en parabel som öppnar sig nedåt är derivatans nollställe funktionens största värde. Det värde vi söker.

Antingen motiverar du eller så jobbar du med ett intervall. Intervallet är \( -50 < t < 80 \).

Det betyder att hastigheten är \( 5000 + 15 \cdot 100 = 6500 \) ark/timme.

Dygnets totala mängd är \( f(15) = 105 625 \) ark.

Akashi Kaikyō är en hängbro i Japan som sammanbinder Kobe på Honsu med Iwaya på ön Awaj. Bron blev färdig 1998 och med sina 1991 m mellan centralspannet var det det längsta i världen för en hängbro. En bild av bron ser du nedan.

Bestäm den största lutningen som bilvägen har på bron. Bilden kan du ladda ner genom att klicka här.

Mera fakta om bron hittar du på Wikipedia.

Vi importerar bilden i GeoGebra och anpassar en funktion.

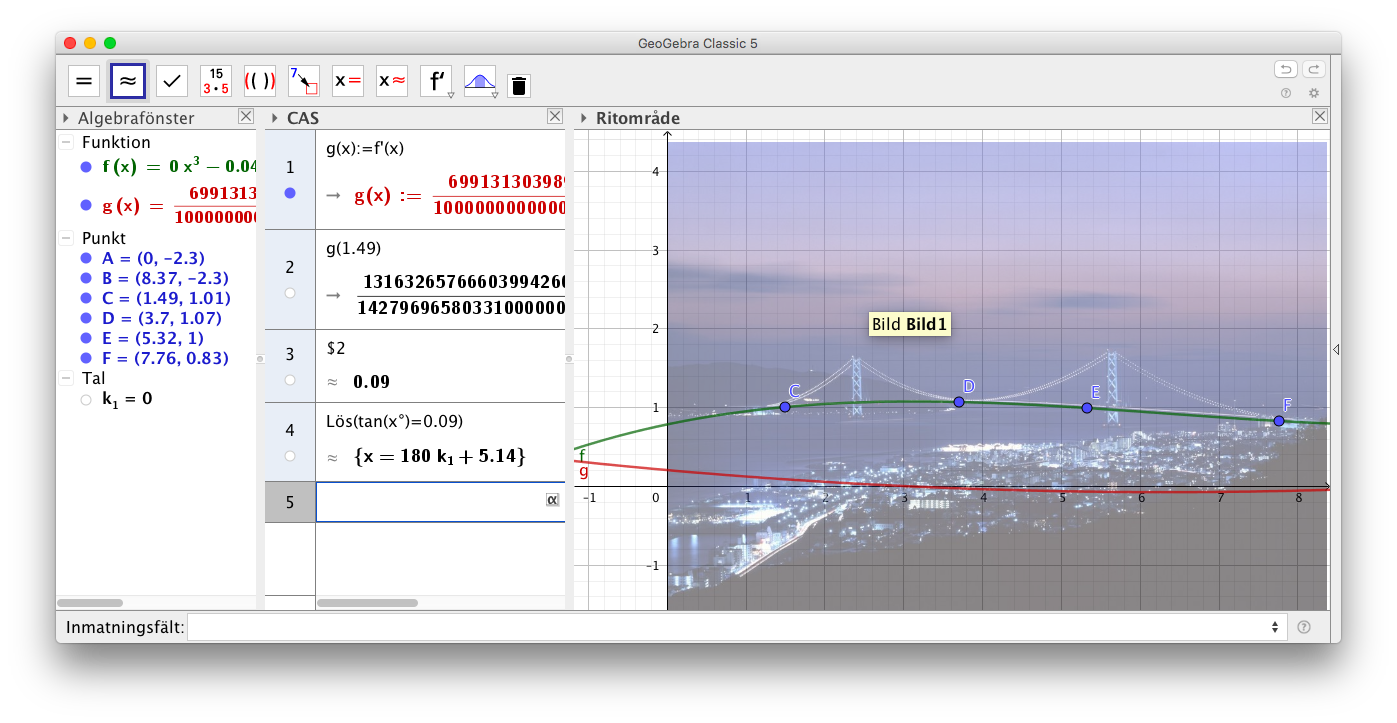
Vi får lutningen 5,1 grader.
Temperaturen en vårdag beskrivs med funktionen \( f(t)=-\dfrac{1}{200} t^{3} + \dfrac{23}{200} t^{2} - \dfrac{51}{100} t + 5 \) där \( t\in [0,24] \).

Bestäm
1. största och minsta temperaturen för vårdagen i fråga.
  
  Derivatafunktionen är \( f(t)=\dfrac{1}{200} (-3 t^{2} + 46 t - 102) \).
  
  Derivatans nollställen \( f'(t)=0 \) är \( t=2,69 \) och \( t=12,64 \).
  
  Eftersom vi har en funktion som begränsas av ett intervall hittar vi största och minsta värden i intervallets ändpunkter eller i de punkter där derivatan har värdet noll.
  
  \( \begin{array}{rcl} f(0) & = & 5\\ f(2,69) & = & 4,36 \\ f(12,64) & = & 6,83\\ f(24) & = & -10,12 \\ \end{array} \)
  
  Högsta temperaturen är 6,8 ^oC och lägsta -10,1 ^oC.
2. Undersök andraderivatan och bestäm vilken tid på dygnet temperaturförändringen är störst.
  
  Vi får \( f''(t)=\dfrac{1}{100} (-3 t + 23 ) \).
  
  Vi söker nollstället för \( f''(t)=0 \) som är \( t=7,67 \).
  
  Eftersom vi har \( t\in [0,24] \) måste vi beakta ändpunkterna för intervallet. Vi sätter in värden i \( f'(t) \).
  
  \( \begin{array}{rcl} f'(0) & = & -0,51\\ f'(7,67) & = & 0,37\\ f'(24) & = & -3,63\\ \end{array} \)
  
  Enheten för temperaturförändringen är \( \dfrac{^{o}\text{C}}{\text{h}} \).
  
  Betyder att klockan 24.00 är temperaturförändringen störst.
Låt \( a_n=n^2-2 \), då \( a\in \mathbb{N} \). Visa att talföljden är strängt växande.

Vi undersöker funktionen \( f(x)=x^2-2 ,\mathbb{R}+\to \mathbb{R} \) och visar att den är strängt växande i sin definitionsmängd.

\( f'(x)=2x \) och \( f'(x)=0 \) då \( 2x=0 \Leftrightarrow x=0 \).

\( f'(1)=2\cdot 1 = 2 \) som betyder att \( f \) är växande. Eftersom \( f' \) saknar andra nollställen än \( x=0 \) och är växande i intervallet så är \( f \) strängt växande i sin definitionsmängd.

Det betyder att \( (a_n) \) är strängt växande.
Låt \( a_n=\dfrac{2}{n^2} \) då \( n=1,2,3,\ldots \). Visa att talföljden är strängt avtagande.

Vi undersöker funktionen \( f(x)=\dfrac{2}{x^2} = 2x^{-2} \), \( \mathbb{R}_+\to \mathbb{R} \) och visar att den är strängt avtagande i sin definitionsmängd.

\( f'(x)=-2(2x^{-3}) = -\dfrac{4}{x^3} \). \( f'(x) \) saknar nollställen eftersom täljaren aldrig får värdet noll.

Då \( f'(1)=-\dfrac{4}{1^3} = -4 \) så är \( f \) avtagande. Eftersom \( f' \) saknar nollställen så är \( f \) strängt avtagande och \( (a_n) \) är strängt avtagande.
Läget för en kropp i röresle får vi genom sambandet \( x(t)=x_0 + v_0 t +\dfrac{1}{2}at^2 \). (Detta samband borde vara bekant från fysiken, kurs 4.)
1. Derivera funktionen \( x(t) \) med avsende på \( t \), tiden. Vad får vi för formel?
  
  \( \dfrac{d}{dt} (x_0 +v_0t +\dfrac{1}{2}at^2) = v_0 +at \).
  
  \( v_0+at \) ger hastigheten för en kropp vid en bestämd tidpunkt, \( t \). Vi kan skriva det som \( v(t)=v_0+at \).
2. Derivera funktionen som du fick i a-fallet. Vad får vi då?
  
  \( \dfrac{d}{dt}(v_0+at) = a \).
  
  Vi har accelerationen vid en bestämd tidpunkt, \( a(t)=a \).