11. Geometrisk tolkning av skalär produkt

Nu tar vi och utgår från vektorer men vi kombinerar dem med cosinussatsen, $a^2=b^2+c^2-2bc\cos\alpha$ , för att komma åt skalära produkten.

Härledning

Vi har $\overline{a}=x_1\overline{i}+y_1\overline{j}+z_1\overline{k}$ och $\overline{b}=x_2\overline{i}+y_2\overline{j}+z_2\overline{k}$ .

Eftersom vi placerar $\overline{a}$ och $\overline{b}$ så att de börjar i samma punkt så är den längre sidan $\mid \overline{a}-\overline{b}\mid$ .

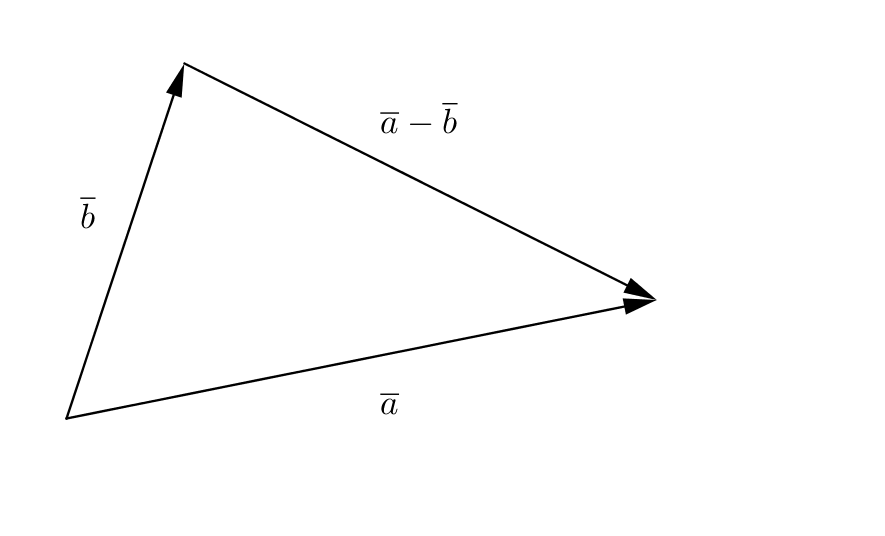
Då vi skriver om cosiunssatsen så att den passar vår triangel får vi att $\mid \overline{a}-\overline{b}\mid^2=\mid\overline{a}\mid^2+\mid\overline{b}\mid^2-2\mid\overline{a}\mid\mid\overline{b}\mid\cos\alpha$ .

Längderna av de kortare sidorna är $\mid \overline{a} \mid ^2 = x_1^2 + y_1^2 + z_1^2$ och $\mid \overline{b} \mid ^2 = x_2^2 + y_2^2 + z_2^2$ .

Kvadraten av den tredje längden är

$\begin{array}{rcl} \mid \overline{a}-\overline{b} \mid ^2 & = & (x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2 \\ & = & x_1^2-2x_1x_2+x_2^2 + y_1^2-2y_1y_2 + y_2^2 + z_1^2 -2z_1z_2+z_2^2 \\ & = & x_1^2+y_1^2+z_1^2 +x_2^2+y_2^2+z_2^2 -2x_1x_2 -2y_1y_2-2z_1z_2 \\ & = & \mid \overline{a} \mid ^2 + \mid \overline{b} \mid ^2 -2(x_1x_2 + y_1y_2+z_1z_2).\\ \end{array}$

När vi jämför hur vi uttryckte cosinussasten med sidorna i vår triangel och hur vi kan uttrycka $\mid\overline{a}-\overline{b}\mid^2$ så märker vi att vi har nästan samma termer. Det som skiljer är $x_1x_2+y_1y_2+z_1z_2$ och $\mid\overline{a}\mid\mid\overline{b}\mid\cos\alpha$ . För att vi skall ha identitet så får vi att

$x_1x_2+y_1y_2+z_1z_2=\overline{a}\cdot \overline{b}=\mid\overline{a}\mid\mid\overline{b}\mid\cos\alpha.$

Det vi får är skalära produkten för två vektorer.

Skalära produkten mellan $\overline{a}$ och $\overline{b}$ får vi som $\overline{a}\cdot\overline{b} = \mid\overline{a}\mid\mid\overline{b}\mid \cos(\overline{a},\overline{b})$ .

Skalära produkten är en operation mellan två vektorer som ger ett värde. Med hjälp av skalära produkten kan vi säga om hur två vektorer förhåller sig till varandra.

Vinkeln mellan två vektorer bestämmer vi som $\cos(\overline{a}, \overline{b}) = \dfrac{\overline{a}\cdot\overline{b}}{\mid\overline{a}\mid\mid\overline{b}\mid}$ .

Vinkeln mellan vektorerna $\overline{a}$ och $\overline{b}$ kan vi uppskatta genom att bilda $\overline{a}\cdot\overline{b}$ . Är

$\overline{a}\cdot\overline{b}<0$ är vinkeln trubbig
$\overline{a}\cdot\overline{b}=0$ är vinkeln rät
$\overline{a}\cdot\overline{b}>0$ är vinkeln spetsig.

Exempel 1 Bestäm vinkeln mellan vektorerna $\overline{a}=\overline{i}-2\overline{j}+\overline{k}$ och $\overline{b}=2\overline{i}+\overline{j}-2\overline{k}$ .

Uppgifter

Bestäm typ av vinkel som följande vektorer bildar. Du behöver inte veta storleken, utan bestäm värdet av den skalära produkten och svara utgående från det.

Påstående	Spetsig	Rät	Trubbig
$3\overline{i}-2\overline{j}$ och $3\overline{i}+\overline{j}$
$4\overline{i}-2\overline{j}$ och $\overline{i}+2\overline{j}$
$\overline{i}-\overline{j}$ och $\overline{j}$
$3\overline{i}-\overline{j}$ och $\overline{i}+2\overline{j}$
$\overline{i}+2\overline{j}$ och $3\overline{i}+\overline{j}$
$-\overline{i}+2\overline{j}$ och $5\overline{i}+\overline{j}$

Påstående	Spetsig	Rät	Trubbig
$3\overline{i}-2\overline{j}$ och $3\overline{i}+\overline{j}$
$4\overline{i}-2\overline{j}$ och $\overline{i}+2\overline{j}$
$\overline{i}-\overline{j}$ och $\overline{j}$
$3\overline{i}-\overline{j}$ och $\overline{i}+2\overline{j}$
$\overline{i}+2\overline{j}$ och $3\overline{i}+\overline{j}$
$-\overline{i}+2\overline{j}$ och $5\overline{i}+\overline{j}$

Bestäm vinkeln mellan följande vektorer med en tiondels grad noggrannhet.
1. $\overline{i}+2\overline{j}$ och $3\overline{i}+2\overline{j}$ .
  
  Vi får
  
  $\overline{a} \cdot \overline{b} = 1\cdot 3 +2\cdot 2 = 7$ .
  
  $\mid \overline{a} \mid = \sqrt{1^2+2^2} = \sqrt{5}$ .
  
  $\mid \overline{b} \mid = \sqrt{3^2+2^2} = \sqrt{13}$ .
  
  $\cos (\overline{a},\overline{b}) = \dfrac{7}{\sqrt{5}\cdot\sqrt{13}}$
  
  Vi får 29,7^o.
2. $\overline{i}+\overline{j}$ och $3\overline{i}-\overline{j}$ .
  
  Vi får
  
  $\overline{a} \cdot \overline{b} = 1\cdot 3 +1(-1) = 2$ .
  
  $\mid \overline{a} \mid = \sqrt{1^2+1^2} = \sqrt{2}$ .
  
  $\mid \overline{b} \mid = \sqrt{3^2+(-1)^2} = \sqrt{10}$ .
  
  $\cos (\overline{a},\overline{b}) = \dfrac{2}{\sqrt{2}\cdot\sqrt{10}}$
  
  Vi får 63,4^o.
3. $-\overline{i}+2\overline{j}$ och $2\overline{i}-\overline{j}$ .
  
  Vi får
  
  $\overline{a} \cdot \overline{b} = -1\cdot 2 +2(-1) = -4$ .
  
  $\mid \overline{a} \mid = \sqrt{(-1)^2+2^2} = \sqrt{5}$ .
  
  $\mid \overline{b} \mid = \sqrt{2^2+(-1)^2} = \sqrt{5}$ .
  
  $\cos (\overline{a},\overline{b}) = \dfrac{-4}{\sqrt{5}\cdot\sqrt{5}}$
  
  Vi får 143,1^o.
Hörnen för triangeln $ABC$ är i punkterna $A = (-13,43)$ , $B = (17,42)$ och $C = (15,-33)$ . Är vinkeln vid punkten $B$ spetsig eller trubbig?

Vi bilar den skalära produkten för $\overline{BA} \cdot \overline {BC}$ och undersöker värdet.

Vi får att $\overline{BA} = -30\overline{i} +\overline{j}$ och $\overline{BC} = --2\overline{i} -75\overline{j}$ . Skalära produkten $\overline{BA} \cdot \overline {BC} = -15$ .

Vinkeln vid $B$ är trubbig \).
En triangel bildas av punkterna $A=(0,-1,-2)$ , $B=(1,0,1)$ och $C =(-2,2,3)$ . Bestäm storleken av vinklarna för triangeln med en tiondels decimals noggrannhet.

Situationen är följande:

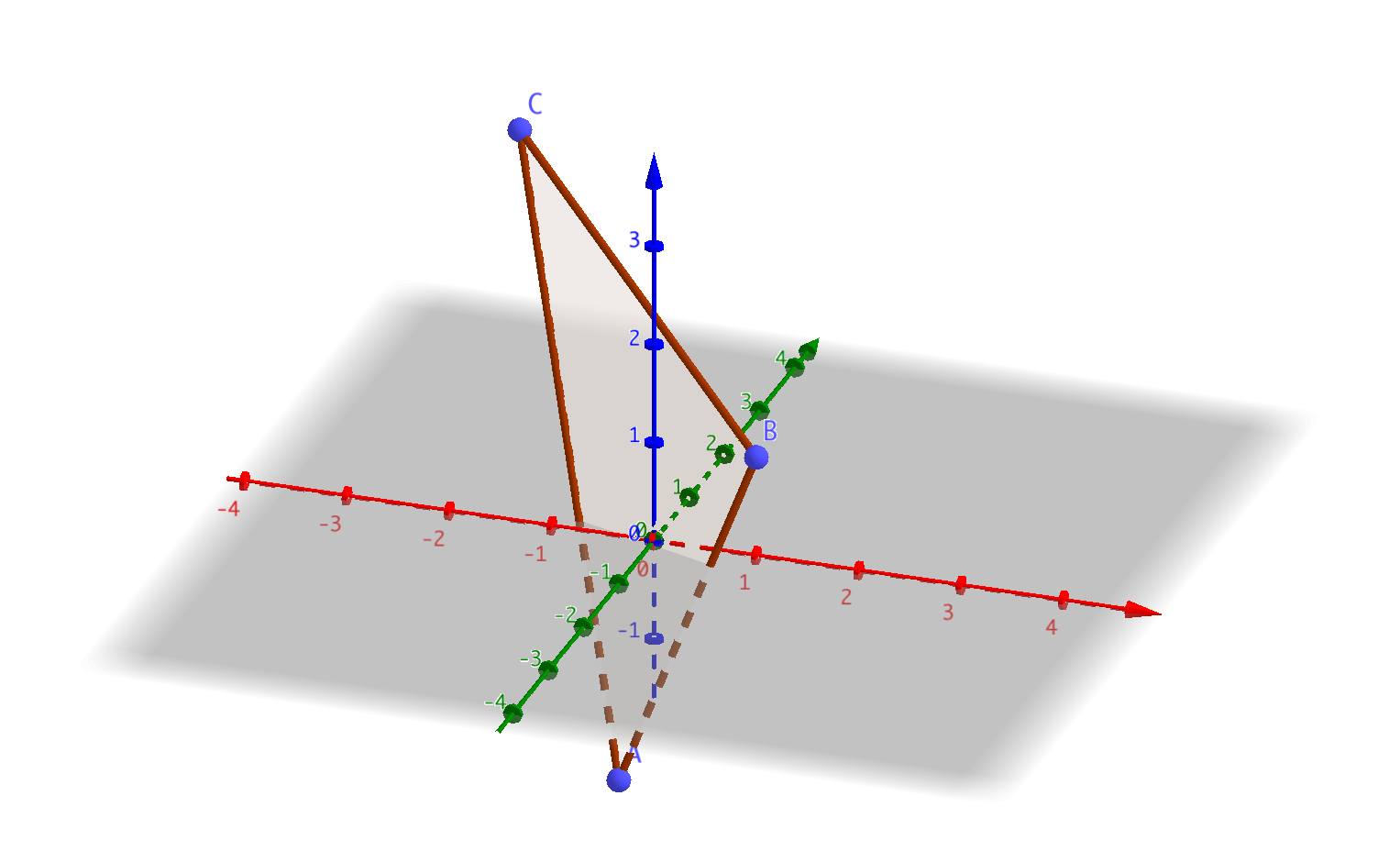
Från figuren ser vi att vinklarna vid A och C är spetsiga medan B är trubbig.

Vi bildar vektorerna.

$\overline{a} = \overrightarrow{AB} = (1-0)\overline{i} + (0-(-1))\overline{j} + (1-(-2))\overline{k} = \overline{i} + \overline{j} +3\overline{k}$

$\overline{b} = \overrightarrow{AC} = (-2-0)\overline{i} + (2-(-1))\overline{j} + (3-(-2))\overline{k} = -2\overline{i} + 3\overline{j} +5\overline{k}$

$\overline{c} = \overrightarrow{BC} = (-2-1)\overline{i} + (2-0)\overline{j} + (3-1)\overline{k} = -3\overline{i} + 2\overline{j} +2\overline{k}$

Längderna av vektorerna är

$\mid \overline{a} \mid = \sqrt{11}$

$\mid \overline{b} \mid = \sqrt{38}$

$\mid \overline{c} \mid = \sqrt{17}$

De skalära produkterna är

$\overline{a} \cdot \overline{b} = 16$

$\overline{a} \cdot \overline{c} = 5$

$\overline{b} \cdot \overline{c} = 22$

Vi får vinklarna

$\angle(\overline{a},\overline{b}) = 38,5^{\circ}$

$\angle(\overline{a},\overline{c}) = 68,6^{\circ}$

$\angle(\overline{b},\overline{c}) = 30,1^{\circ}$

Eftersom vi får den mindre vinkeln med hjälp av skalära produkten är vinkeln $\angle(\overline{a},\overline{c}) = 180^{\circ} - 68,6^{\circ} = 111,4^{\circ}$ .

Triangelns vinkelsumma är 38,5^o+111,4^o+30,1^o = 180^o.
I triangeln $ABC$ gäller att $\overline{AB} = 3\overline{i} + \overline{j} - \overline{k}$ och $\overline{AC} = \overline{i} - \overline{j} + \overline{k}$ . Bestäm storleken av vinklarna i triangeln med en grads noggrannhet.

Vi får $\measuredangle A \approx 80^{\circ}, \measuredangle B \approx 29^{\circ}$ och $\measuredangle C \approx 71^{\circ}$ .
För vilket värde på $k$ har vinkeln mellan $\overline{a}=2\overline{i}-2\overline{j}$ och $\overline{b}=k\overline{i}-2\overline{j}$ värdet $45^{\circ}$ ?

$\cos 45^{\circ} = \dfrac{\sqrt{2}}{2} = \dfrac{1}{\sqrt{2}}$ .

$\overline{a} \cdot \overline{b} = 2\cdot k -2\cdot 2 = 2k-4$ .

$\mid \overline{a} \mid = \sqrt{2^2+(-2)^2} = \sqrt{8}$ .

$\mid \overline{b} \mid = \sqrt{k^2+(-2)^2} = \sqrt{k^2+4}$ .

Vi får ekvationen

$\dfrac{1}{\sqrt{2}} = \dfrac{2k-4}{\sqrt{8}\cdot\sqrt{k^2+4}}$

Antingen löser vi ekvationen genom att kvadrera, $\dfrac{1}{2} = \dfrac{(2k-4)^2}{8(k^2+4)}$ eller på räknare.

Vi får $k= 0$ .
För parallellogrammen ABCD gäller att diagonalvektorerna $\overrightarrow{AC}=6\overline{i}+2\overline{j}$ och $\overrightarrow{DB}=2\overline{i}-2\overline{j}$ . Bestäm storleken av vinklarna i parallellogrammen med noggrannheten en tiondels grad.

Situationen är följande:

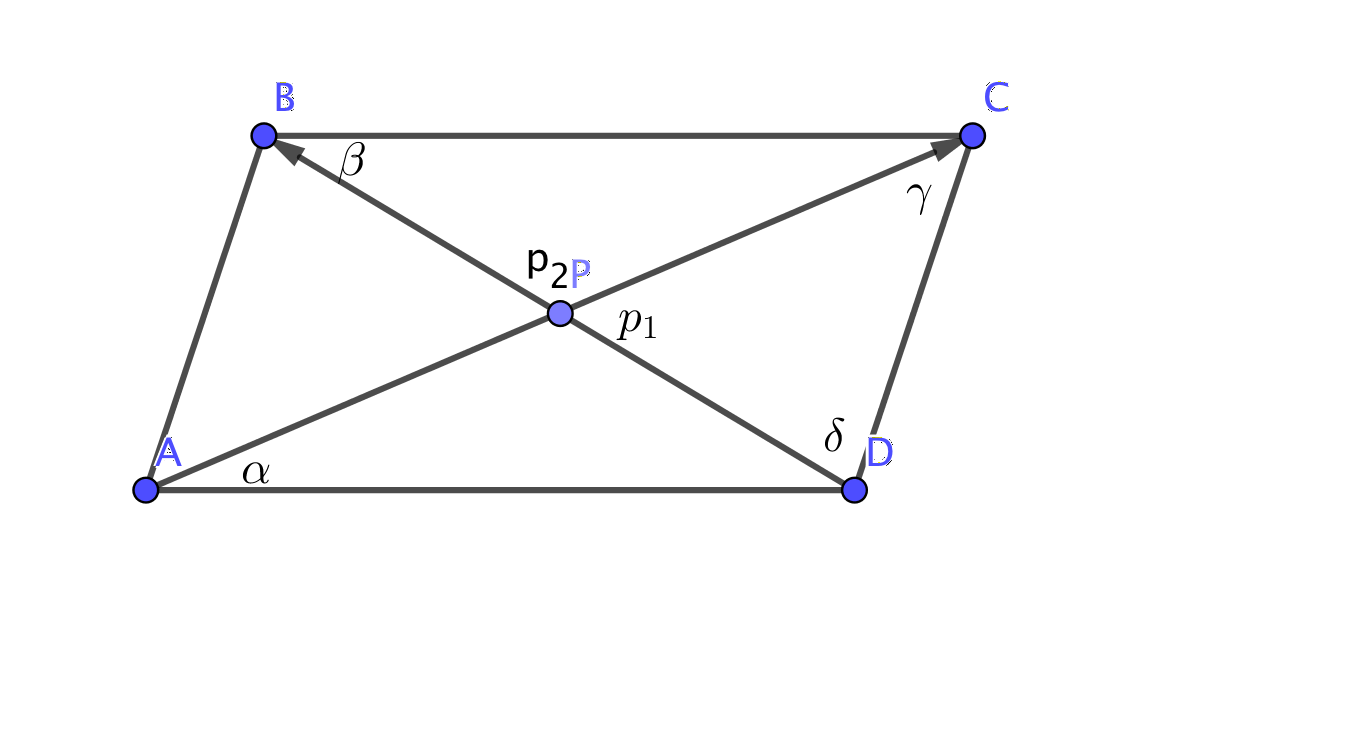
Riktningskoefficienten för diagonalen $AC = \dfrac{2}{6} =\dfrac{1}{3}$ . Vi har $k = \tan \alpha$ . Lutningen är 18,43^o. Det är frågan om vinlen $\alpha$ .

Riktningskoefficienten för diagonalen $DB = \dfrac{-2}{2} = -1$ . Lutningen är -45^o. Då är $\beta = 45^{\circ}$ .

HÄR!!!

Det betyder att $\alpha + \gamma + \delta = 135^{\circ}$ .

Vinkeln mellan diagonalerna är 63,43 grader. Det är frågan om $p_1$ . Se till att du bestämmer den!

Då är vinkeln $p_2 = 180^{\circ} - 63,43^{\circ} = 116,57^{\circ}$ .

Vi bildar följande samband.

$\alpha = 18,43^{\circ}$

$\beta + \alpha + 116,57^{\circ} = 180^{\circ}$

$\delta + \gamma + 63,43^{\circ} = 180^{\circ}$

$\alpha + \beta + \gamma + \delta = 180^{\circ}$

Storleken av den mindre vinkeln är $45^{\circ}$ och den större är $135^{\circ}$ .
För vilka värden på $k$ är triangeln som bestäms av punkterna $(0,3)$ , $(3,4)$ och $(1,k)$ spetsig i vinkeln som bildas i $(1,k)$ ?

Vilka värden har skalära produkten av en spetsig vinkel? Bilda modigt en olikhet.

Vi namnger punkterna $A= (0,3)$ , $B=(3,4)$ och $C=(1,k)$ .

Vi bildar vektorerna som vi behöver.

$\overrightarrow{CA} = (0-1)\overline{i} + (3-k)\overline{j} = -\overline{i} + (3-k)\overline{j}$

$\overrightarrow{CB} = (3-1)\overline{i} + (4-k)\overline{j} = 2\overline{i} + (4-k)\overline{j}$

Vinkeln skall vara spetsig. Det betyder att den skalära produkten skall ha positiva värden. Vi bildar en olikhet, $-1\cdot 2 + (3-k)(4-k) > 0$ .

Olikeheten löser du för hand eller på räknare. Då $k < 2$ eller då $k > 5$ .
En linje går genom punkterna (−1,0,3) och (1,3,2). Bestäm storleken av vinkeln som linjen bildar med följande plan.
1. $xy$ -planet.
  
  Riktningsvektorn för linjen är $\overline{s} = (-1-1)\overline{i} + (0-3)\overline{j} + (3-2)\overline{k} = -2\overline{i} -3\overline{j} + \overline{k}$ .
  
  Eller så kommer du till $\overline{s} = 2\overline{i} +3\overline{j} - \overline{k}$ .
  
  Den vektor som är i $xy$ -planet och har samma riktning är $\overline{a} = -2\overline{i} -3\overline{j}$ .
  
  Vi bestämmer vinkeln mellan dessa.
  
  $\overline{a} \cdot \overline{s} = -2(-2) -3(-3) + 0\cdot 1 = 13$ .
  
  $\mid \overline{a} \mid = \sqrt{2^2+(-3)^2} = \sqrt{13}$ .
  
  $\mid \overline{s} \mid = \sqrt{(-2)^2+(-3)^2+1^2} = \sqrt{14}$ .
  
  $\cos (\overline{a},\overline{s}) = \dfrac{13}{\sqrt{13}\cdot\sqrt{14}}$
  
  Vinkeln är $15,5^{\circ}$ .
2. $yz$ -planet.
  
  Den vektor som är i $yz$ -planet och har samma riktning är $\overline{a} = -3\overline{j} +\overline{k}$ .
  
  Vi bestämmer vinkeln mellan dessa.
  
  $\overline{a} \cdot \overline{s} = -2\cdot 0 -3(-3) + 1\cdot 1 = 10$ .
  
  $\mid \overline{a} \mid = \sqrt{(-3)^2+1^2} = \sqrt{10}$ .
  
  $\mid \overline{s} \mid = \sqrt{(-2)^2+(-3)^2+1^2} = \sqrt{14}$ .
  
  $\cos (\overline{a},\overline{s}) = \dfrac{10}{\sqrt{10}\cdot\sqrt{14}}$
  
  Vinkeln är $32,3^{\circ}$ .
Ett flygplan startar från punkten $(2,4,0)$ och lyfter i riktningen $2\overline{i}+3\overline{j}+\overline{k}$ . Hur stor vinkel bildar flygplanets rutt mot marken? Svara med noggrannheten 0,1 grader.

Rita bild och fundera. Hur kan du uttrycka den vektor som går längs med marken och beskriver planets rutt?

Vektorn som beskrivers flygplanets rutt längd med marken är $\overline{s} = 2\overline{i}+3\overline{j}$ .

Vektorn som beskriver flygplanets rutt är $\overline{a}= 2\overline{i}+3\overline{j}+\overline{k}$ .

Vi bestämmer vinkeln mellan dessa.

$\overline{a} \cdot \overline{s} = 2\cdot 2 +3\cdot 3 + 1\cdot 0 = 13$ .

$\mid \overline{a} \mid = \sqrt{2^2+3^2+1^2} = \sqrt{14}$ .

$\mid \overline{s} \mid = \sqrt{2^2+3^2} = \sqrt{13}$ .

$\cos (\overline{a},\overline{s}) = \dfrac{13}{\sqrt{14}\cdot\sqrt{13}}$

Vinkeln är $15,5^{\circ}$ .