18. Sfären

Volymen för sfären eller klotet är \( V=\dfrac{4\pi r^3}{3} \) och den totala arean för sfären är \( 4\pi r^2 \).

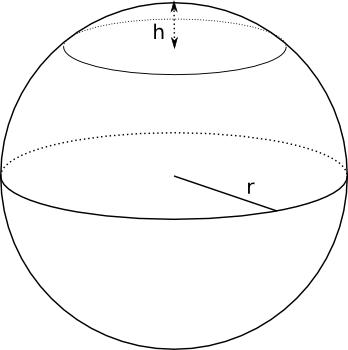
Volymen av ett klotsegment fås via \( V=\pi h^2(r-\dfrac{h}{3}) \) och arean för kalotten är \( A=2\pi rh \) där \( h \) är höjden för kalotten.

Exempel 1 En hur lång sträcka skulle vi färdas runt jorden om vi skulle färdas längs den 65 breddgraden?

Lösning

Vi betecknar \( x \) radien vinkelrät mot jordens radie vid 65 breddgraden. För att får ett värde på \( x \) tillämpar vi trigonometri.

\( \begin{array}{rl} \textrm{Vi får att } \sin 25^{\circ} & = \dfrac{x}{6370} \\ \\ x & = 6370 \sin25^{\circ} = 2692 \textrm{ km} \\ \textrm{Omretsen är } 2\pi \cdot x & = 2\pi \cdot 2692 = 16914 \approx 17000 \textrm{ km} \\ \end{array} \)

Exempel 2 Bestäm arean av den del av jorden som är norr om 60 breddgraden.

Lösning

Vi börjar på motsvarande sätt som ovan.

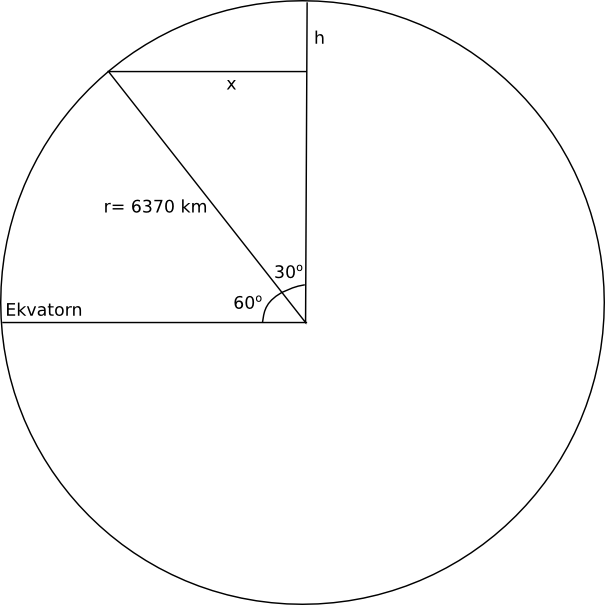
Vi får att

\( \begin{array}{rl} \cos 30^{\circ} & = \dfrac{x}{6370} \\ \\ x & = 6370 \cos 30^{\circ} \\ \textrm{Höjden för kalotten får vi som } h & = r-x = 6370 - 6370\cos 30^{\circ} \\ \textrm{Och hela arean som } A & = 2\pi r h = 2 \pi \cdot 6370 (6370 - 6370\cos 30^{\circ}) \\ & = 34157116 \approx 34 200 000 \textrm{ km}^2 \\ \end{array} \)

Uppgifter

En fotboll har radien 11 cm. Bestäm arean och volymen för bollen.

Arean är \( A = 4\pi r^2 = 4\pi (11 \text{ cm})^2 = 484\pi \approx 1520 \text{ cm}^2 \).

Volymen är \( V = \dfrac{4}{3}\pi r^3 = \dfrac{4}{3} \pi (11 \text{ cm}^3)^3 = 5575,27\ldots = 5600 \text{ cm}^3 \).
Beräkna radien för en strandboll om bollens
1. area är 4070 cm².
  
  Vi har \( A = 4\pi r^2 \).
  
  Vi får ekvationen \( 4070 = 4\pi r^2 \), alltså \( r = \sqrt{\dfrac{4070}{4\pi}} = 17,99\ldots \approx 18,0 \) cm.
2. Volym är 74 liter.
  
  Vi har \( V = \dfrac{4}{3}\pi r^3 \).
  
  1 liter motsvaras av 1 dm³. Vi räknar med det och får radien som dm.
  
  Vi får ekvationen \( 74 = \dfrac{4}{3} \pi r^3 \), alltså \( r = \sqrt[3]{\dfrac{3\cdot 74}{4\pi}} = 2,6044\ldots \approx 2,60 \) dm. Alltså 26,0 cm.
Hur många glasskulor med diametern 6,0 cm får man ur ett 1 liters paket om vi räknar med att vi kan utnyttja all glass?

Kom ihåg att 1 liter = 1 dm³.

Volymen för ett klot, \( V=\dfrac{4}{3}\pi r^3 = \dfrac{4}{3}\pi 0,3^3 = 0,1130\ldots dm^3 \).

Antal bollar \( \dfrac{1 \text{ dm}}{0,1130\ldots \text{ dm}^3} = 8,8 \) st.

Alltså 8 st hela.
Diametern för en oskalad apelsin är 9,0 cm. Skalets tjocklek är 0,5 cm. Hur många procent av apelsinens volym är skal?

Hela apelsinens volym är \( V=\dfrac{4}{3}\pi 4,5^3 = 381,70\ldots \) cm³.

Volymen utan skal är \( V=V=\dfrac{4}{3}\pi 4^3 = 268,08\ldots \) cm³.

Den procentuella andelen skal är \( \dfrac{381,70\ldots - 268,08\ldots}{381,70\ldots} = 0,29766 \).

Alltså 29,8 %.
En tub för tennisbollar fylls med fyra tennisbollar. Hur många procent tomrum finns det i tuben?

Volymen för cylindern är \( \pi r^2 \cdot 8r \).

Volymen för en tennisboll är \( \dfrac{4}{3}\pi r^3 \).

Förhållandet mellan volymenrna är \( \dfrac{4\cdot\dfrac{4}{3}\pi r^3}{\pi r^2 \cdot 8r} = 0,666\ldots \).

Andelen tomrum är \( 1-0,666\ldots = 0,333 \). Alltså 33,3 %.
Totala arean för en fotboll är 15,6 dm². Bestäm volymen av fotbollen.

Vi har att \( A=4\pi r^2 \), alltså \( r=\sqrt{\dfrac{A}{4\pi}} = \sqrt{\dfrac{15,6}{4\pi}} = 1,114\ldots \) dm.

Volymen är \( V=\dfrac{4}{3} \pi \cdot 1,114\ldots^3 = 5,793\ldots \) dm³.

Alltså 5,8 dm³
En kub inskrivs i en sfär. Hur stor många procent utgör kubens volym av sfärens volym?

Vi betecknar radien med \( r \) och halva sidan för kuben med \( a \). Då får vi att \( a=\sqrt{r} \), alltså \( r=\dfrac{a}{\sqrt{2}} \).

Förhållandet är \( \dfrac{V_{\text{kub}}}{V_{\text{sfär}}} = \dfrac{(2a)^3}{\dfrac{4}{3}\pi (\dfrac{a}{\sqrt{2}})^3} = \dfrac{2}{\pi\sqrt{3}} = 0,36755 \).

Alltså 36,8 %.
I en rak kon vars höjd är dubbelt så lång som diametern för bottenarean inskrivs största möjliga sfär. Bestäm förhållandet mellan sfärens och konens volymer med en tusendels decimals noggrannhet.

0,476