MaA 3 Geometri

13. Rätblock

Som det sista för kursen tar vi ännu och ser på 3 dimensionella kroppar. Kroppar som har längd, bredd och höjd.

Volymen för ett rätblock är längden gånger bredden gånger höjden för rätblocket. Ytan för rätblocket får vi om vi adderar ihop arean för alla sidor.

\( V=abc \)

\( A=2(ab+bc+ac) \)

Rymddiagonalen för ett rätblock får vi som \( d=\sqrt{a^2+b^2+c^2}. \)

Exempel 1 Ett klassrum är 10,0 m långt, 5,0 meter brett och 4,0 meter högt.

  1. Bestäm volymen för rummet.
  2. Bestäm rymddiagonalen för rummet.
  3. Hur stor area utgör väggarna?

Lösning

  1. Volymen för rummet är \( V = abc=10 \cdot 5 \cdot 4 = 200 \textrm{ m}^3 \).
  2. Rymddiagonalen för rummet är \( d = \sqrt{a^2+b^2+c^2} = \sqrt{10^2+5^2+4^2} = \sqrt{141} \approx 11,9 \textrm{ m} \).
  3. Väggarnas totala area är \( A = 2 \cdot 10 \cdot 4 + 2 \cdot 5 \cdot 4 = 120 \textrm{ m}^2 \).

Exempel 2 Ett rätblock förstoras så att längden av sidorna blir 3 gånger längre. Hur mycket större blir volymen? Hur mycket ökar volymen om vi förstorar rätblocket 9 gånger?

Lösning

Den nya kroppen består av \( 27 =3^3 \) st rätblock. Ökar vi sidorna för rätblocket 9 gånger ökar volymen \( 9^3 = 729 \).

Uppgifter

  1. Ordna längderna, areorna och volymerna i rätt ordning så att den största prefixet kommer överst.
    1. Välj bland följande:
      cm
      dam
      dm
      hm
      km
      m
      mm
      BeteckningOrdning
      1.
      2.
      3.
      4.
      5.
      6.
      7.

      BeteckningOrdning
      km 1.
      hm 2.
      dam 3.
      m 4.
      dm 5.
      cm 6.
      mm 7.
    2. Välj bland följande:
      ar
      cm2
      dm2
      hektar
      km2
      m2
      mm2
      BeteckningOrdning
      1.
      2.
      3.
      4.
      5.
      6.
      7.

      BeteckningOrdning
      km2 1.
      hektar 2.
      ar 3.
      m2 4.
      dm2 5.
      cm2 6.
      mm2 7.
    3. Välj bland följande:
      cm3
      dam3
      dm3
      hm3
      km3
      m3
      mm3
      BeteckningOrdning
      1.
      2.
      3.
      4.
      5.
      6.
      7.

      BeteckningOrdning
      km3 1.
      hm3 2.
      dam3 3.
      m3 4.
      dm3 5.
      cm3 6.
      mm3 7.

  2. Välj rätt samband mellan rymdmåtten.

    Påstående

    1000 liter

    10 liter

    1 liter

    		1 dl 10 ml 1 ml
    1 m3
    1 dm3
    1 cm3
    10 dm3
    0,1 dm3
    10 cm3
    0,01 m3
    0,001 m3
    1000 cm3

    Påstående

    1000 liter

    10 liter

    1 liter

    		1 dl 10 ml 1 ml
    1 m3
    1 dm3
    1 cm3
    10 dm3
    0,1 dm3
    10 cm3
    0,01 m3
    0,001 m3
    1000 cm3

  3. Bestäm volymen och den totala arean för ytan av figuren nedan.

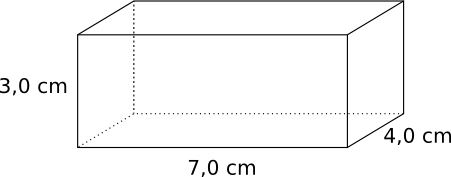
    Volymen är \( 3,0 \cdot 4,0 \cdot 7,0 = 84,0 \) cm3.

    Totala arean är \( A = 2(3,0 \cdot 4,0 + 3,0\cdot 7,0 + 4,0\cdot 7,0) = 122 \) cm2.

  4. En låda är 30 cm bred och höjden är 20 cm. Bestäm längden för lådan då volymen är 30 liter.

    Vi får ekvationen \( 3 \cdot 2 \cdot l = 30 \) som har lösningen \( l=5 \) dm.

  5. När man arbetar med geometri i 3 dimensioner kan det hjälpa att man skapar en bra bild som hjälper på vägen. I GeoGebra finns en funktion för att rita i 3 dimensioner.

    Öppna GeoGebra och plocka fram Ritområde 3D.

    Bekanta dig med verktygen och med hur du roterar arbetsytan.

    1. Skapa en kub med sidan 3.
    2. Skapa ett prisa som inte är vinkelrätt mot bottenytan.
    3. Skapa en kon som placeras på kuben.
    4. Pricka in rymddiagonalen för kuben.
    5. Ändra vyn så att man lätt förstår vad du gjort.

    Någonting i stil med

  6. Ett rum är 2,5 m högt, 4,5 m långt och 4,0 m brett. Till rummet kommer man genom en dörr som är 2,1 m hög och 0,6 m bred och på ena väggen är ett fönster som är 1,5 m brett och 1,8 m högt. Hur många liter målfärg går det åt då en målare skall måla väggarna 2 gånger och åtgången för målfärg är 10-12 m2/l?

    Den totala arean är \( 2(4,5 \text{ m} \cdot 2,5 \text{ m}) + 2(4,0\text{ m} \cdot 2,5 \text{ m}) - (2,1 \text{ m} \cdot 0,6 \text{ m} + 1,5 \text{ m} \cdot 1,8 \text{ m}) = 38,54 \text{ m}^2 \).

    Eftesom den totala arean är 38,54 m2 behöver vi målfärg för 77,08 m2.

    10 m2/liter ger 7,7 l och 12 m2/liter ger 6,4 liter. Det är bättre att ha för mycket målfärg än för litet, därför svar kring 8 liter.

  7. Volymen för en låda är 9 liter. Bestäm längderna för sidorna då förhållandet mellan sidorna är 1:2:3.

    Vi betecknar den kortaste sidan med \( a \). Då är de andra \( 2a \) och \( 3a \).

    Vi får uttrycket \( 9 = a \cdot 2a \cdot 3a \).

    Kortaste är 11,4 cm, mellersta 22,9 cm och den längsta är 34,3 cm.

  8. Hur hög bör en låda vara om man vill få en pinne som är 80,0 cm lång att rymmas i lådan då bottnet är 60,0 cm x 50,0 cm?

    Rymddiagonalen bestäms via \( d = \sqrt{a^2+b^2+c^2} \). Ekvationen blir \( 8 = \sqrt{6^2 +5^2+ c^2} \) som har lösningen \( c= \sqrt{3} \text{ dm} = 17,3205\ldots \text{ cm} \).

    Alltså 17,3 cm.

  9. I en miniatyrmodell av ett hus är huset 40,0 cm långt. I verkligheten blir huset 15,0 m långt.
    1. Hur många m2 är vardagsrummet i verkligheten då det i miniatyren är 320 cm2.

      Vi får förhållandet \( (\dfrac{150 \text{ dm}}{4 \text{ dm}})^2 = \dfrac{x}{3,2 \text{ dm}^2} \) som har lösningen \( x=4500 \text{ dm}^2 = 45 \text{ m}^2 \).

    2. Bestäm volymen för bastun i modellen då bastun i verkligheten är 18,8 m3

      Vi bildar förhållandet \( (\dfrac{4 \text{ dm}}{150 \text{ dm}})^3 = \dfrac{x}{18800 \text{dm}^3} \) som har lösningen \( x=0,3565\ldots \text{ dm}^3 = 360 \text{ cm}^3 \).

  10. Bestäm volymen och rymddiagonalen för ett valfritt utrymme. Hur stor blir volymen om du gör en miniatyrmodell av rummet där längden av sidorna är 1/13-del?

    Lösningen