14. Kuben
Kuben är ett specialfall av rätblocket där alla sidor är lika långa. Det betyder att vi kan bestämma volymen som \( V=a^3 \) och totala arean som \( A=6a^2 \).
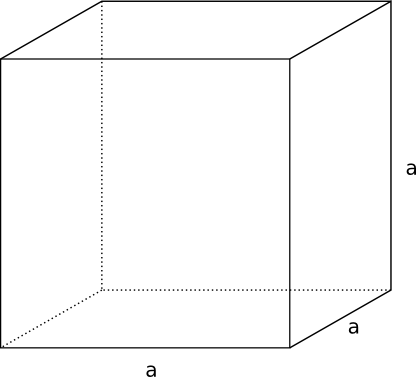
Exempel 1 Bestäm volymen för figuren som består av två kuber där den större kuben har sidan a.
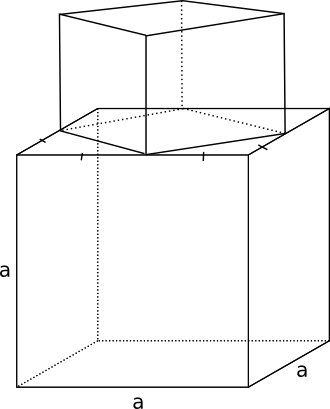
Lösning
\( \begin{array}{lrcll} \textrm{Sidan i den mindre kuben:} & s^2 & = & (\dfrac{a}{2})^2+(\dfrac{a}{2})^2 & \textrm{} \\ \\ \textrm {} & & = & \dfrac{a^2}{4} +\dfrac{a^2}{4} & \textrm{} \\ \\ \textrm {} & & = & \dfrac{2a^2}{4}=\dfrac{a^2}{2} & \textrm{} \\ \\ \textrm {} & s & = & \dfrac{a}{\sqrt{2}} & \textrm{} \\ \\ \textrm {} & V & = & s^3 +a^3 = (\dfrac{a}{\sqrt{2}})^3 + a^3 = \dfrac{a^3+2\sqrt{2}a^3}{2\sqrt{2}} & \\ \end{array} \)
Uppgifter
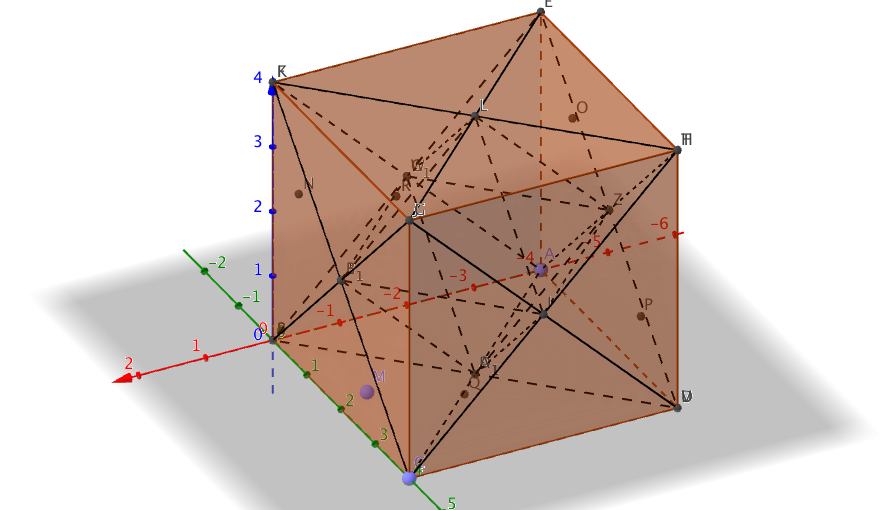
- Rita på GeoGebra följande: Rita en kub och bilda mittpunkterna på kubens sidor genom att rita ut diagonalerna. Sammanbind mittpunkterna för kubens sidor. Vilken figur får vi?
Med hjälplinjer och punkter
och utan hjälplinjer
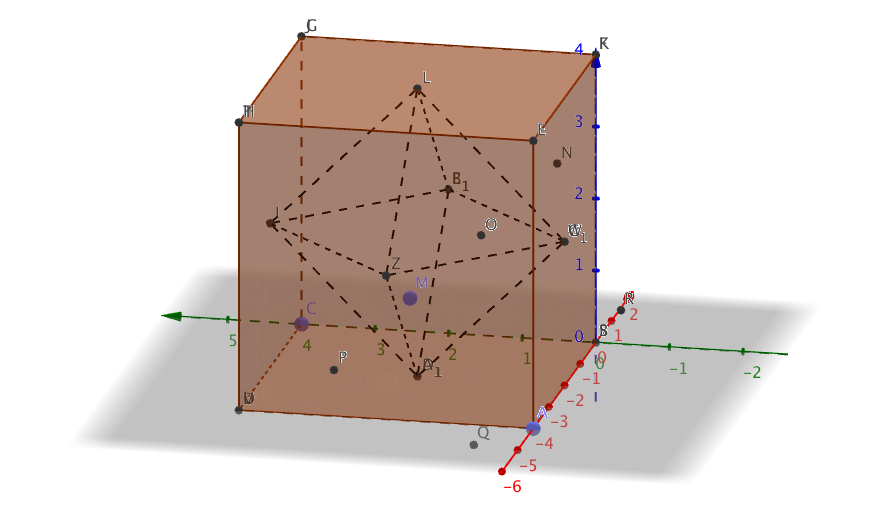
Figuren heter Oktaeder.
- Bestäm den totala arean för en kub vars volym är 8 dm3.
Sidan för längden är \( a = \sqrt[3]{V} = \sqrt[3]{8} = 2 \text{ dm} \).
Totala arean är \( A = 6a^2 = 6\cdot 2^2 = 24 \text{ dm}^2 \).
- En sexsidig tärning målas om. Sidan i träningen är 1,2 cm. Hur mycket målfärg behövs för två omgångar då 1 liter målfärg räcker till 8-10 m2?
Den totala arean för tärningen är \( 6 \cdot (1,2 \text{ cm} )^2 = 8,64 \text{ cm}^2 \).
Då den skall målas två gånger är totala arean 17,28 cm2.
8-10 m2/l betyder 800-1000 dm2/10 dl som är 80000-100000 cm2/100 cl, alltså 800-1000 cm2/1 cl.
Vi får \( \dfrac{17,28}{800} = 0,0216 cl \) och \( \dfrac{17,28}{1000} = 0,01728 cl \).
Alltså ca 0,02 cl som är samma som 0,2 ml. Det är mycket, mycket lite.
- Diagonalen för en kubs sida är \( 3\sqrt{2} \) lång. Bestäm volymen för kuben.
Vi kan lösa den med hjälp av Pythagoras eller Typtrianglar.
Pythagoras sats ger oss att \( s^2 + s^2 = (3\sqrt{2})^2 \). Sidan har längden \( s = 3\). Volymen är då \( V = s^3 = 3^3 = 27 \) v.e.
Genom att utnyttja Typtrianglarna får vi följande lösning:
Då diagonalen har längden \( 3\sqrt{2} \) är sidan 3 lång. Då är volymen \( 3^3 = 27 \) v.e.
- Sidan i en kub med längden \( a \) görs tre gånger längre.
- Hur många gånger större blir volymen?
\( 3^3 = 27 \)
- Hur många gånger längre blir rymddiagonalen?
Rymddiagonalen ändras lika mycket som sidan ändras. Alltså 3 gånger.
- Hur mycket ändras vinkeln mellan rymddiagonalen och ytan under rymddiagonalen?
Inte alls. Förhållandet mellan sidorna hålls samma.
- Hur många gånger större blir volymen?
- Bestäm längden av rymddiagonalen för en kub med sidan \( a \). Hur stor vinkel bildar rymddiagonalen med bottenytan?
Vi får att rymddiagonalen \( d = \sqrt{a^2 + a^2 + a^2} = a\sqrt{3} \).
Vi får \( \cos \alpha = \dfrac{a \sqrt{2}}{a\sqrt{3}} \Leftrightarrow \alpha = 35,26^{\circ} \).