Här hittar du sådant som är till nytta med tanke på dina skrivningar, kommandon för GeoGebra och TI-nSpire CAS och kommandon för Latex.
I GeoGebra ser vi på följande vyer,
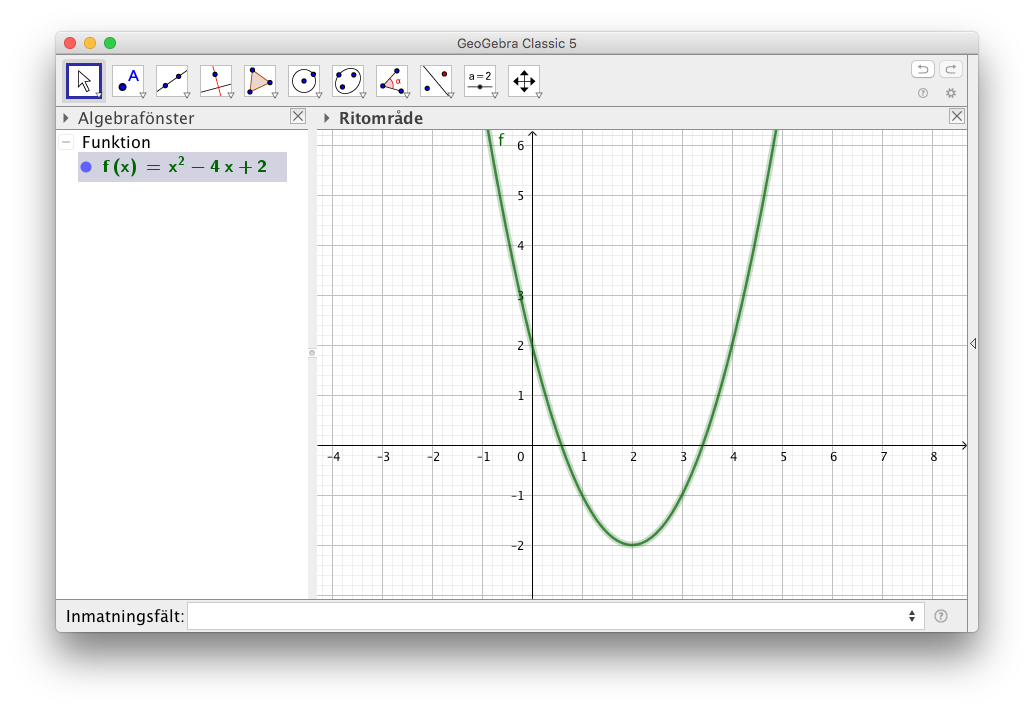
Detta är vyn som du vill ha då du snabbt skall rita en funktion och se hur den beter sig. I Inmatningsfältet skriver du funktionen och så ritas den upp i Ritområdet.

Efter att du har ritat ut den kan du ändra på uttrycket genom att dubbelklicka på funktionens uttryck i Algebrafönstret.
Då du arbetar med CAS kan du utföra uträkningar, så som lösa ekvationer, bestämma funktionsvärden mm.
CAS får du fram genom att välja Visa och CAS.
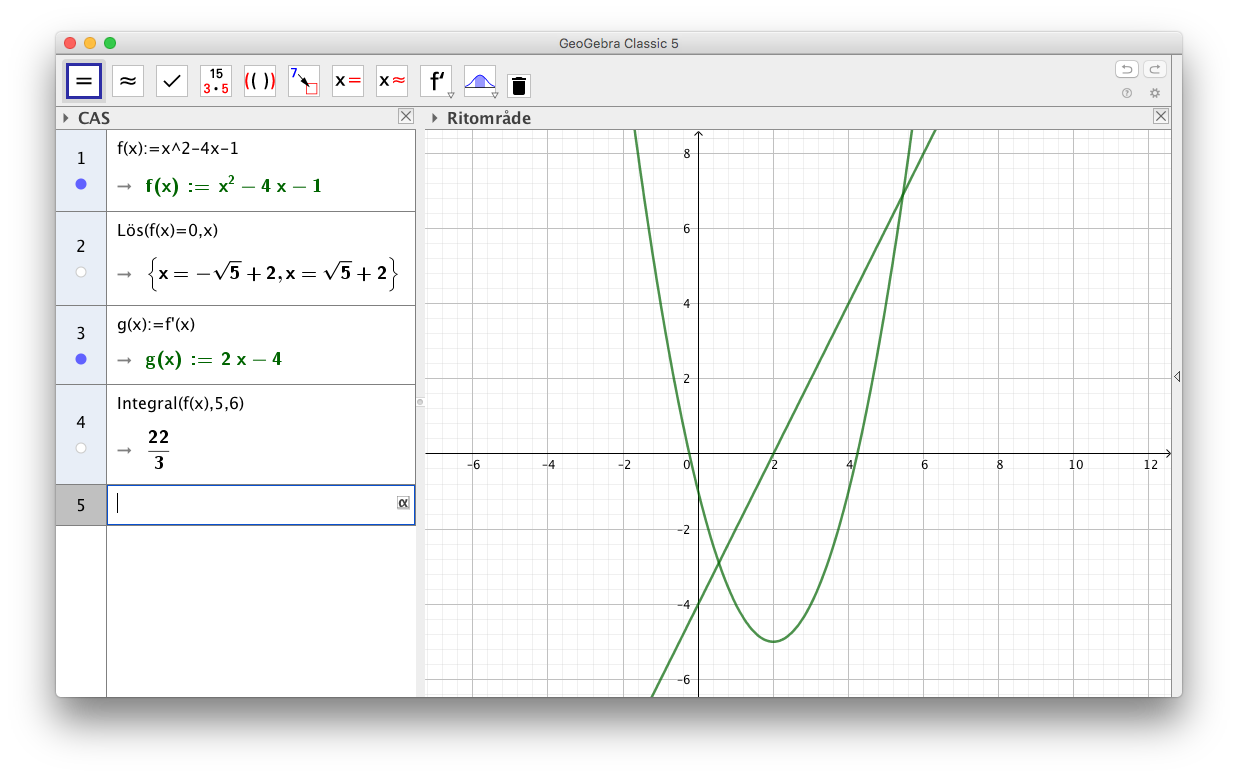
En funktion definierar du med kommando, :=, tex f(x):=x^2-4x-1.
Funktionsvärdet i en punkt beräknar du med att skriva in, f(2), det ger funktionsvärdet i punkten 2.
Vill vi lösa en ekvation, tex nollställena, använder vi oss av lös(), tex, lös(f(x)=0,x). ,x i slutet berättar att vi vill att ekvationen löses med avsende på x.
Vill vi undersöka en olikhet är det samma lös kommando, då ändrar vi = till < eller >.
Derivering sker med kommandot f', tex f'(x). Vill vi spara derivatafunktionen så måste vi definiera en funktion för den, tex g(x):=f'(x).
Integraler sker med kommandot Integral, tex Integral(f(x), 5, 6).
Med sannolikhetsfunktionen kan du lätt arbeta med sannolikhetsfördelingar.
Du får fram Sannolikhetkalkylator under Visa och Sannolikhetskalkylator.
Vid rullgardinen kan du välja mellan olika fördelningar. I gymnasiet klarar du dig bra med Normalfördeling och Binomialfördelning.
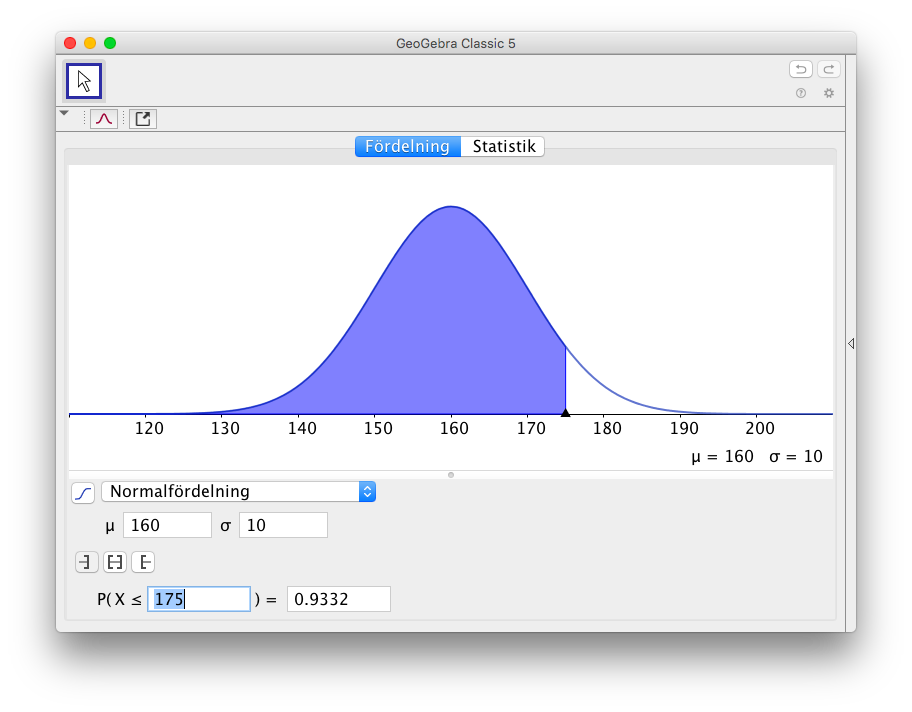
För normalfödelningen fyller du i väntevärdet, \( \mu \) och standardavvikelsen, \( \sigma \). Vid raden P(...) räknar GeoGebra ut sannolikheten åt dig.
Vi antar att vi har en population vars väntevärde är 160 cm och standardavvikelsen 10 cm. Frågan är att hur stor andel är kortare än 175 cm? Vi fyller i parametrarna och får svaret 93,3%.
Genom att klicka på knappen vid rullgardninen får du fram den kumulativa funktionen.
För binomialfördelningen fyller du i antalet, n och sannolikheten, p.
Vi tänker att vi spelar stryktipset. Vi har 13 rader och med sannolikheten 0,33 kan vi få 1, X eller 2. Då vi fyller i de värdena får vi fram sannolikheterna för de olika fördelningarna.
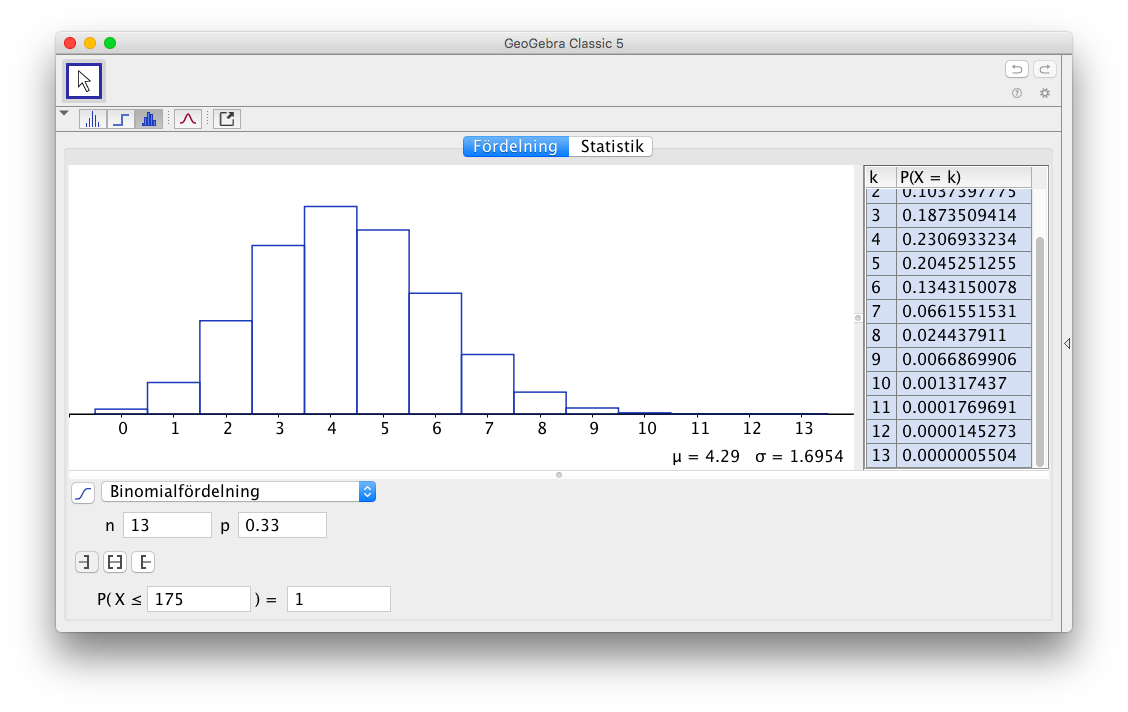
Vi märker att 4 rätt har den största sannolikheten och för att ha 12 eller 13 rätt så är sannolikheten nära 0. För att få fram den måste vi visa mera decimaler, Inställningar och Antal decimaler.
Motsvarande formel editor som används i Abittimiljön hittar du på https://math-demo.abitti.fi/sv.
Med den kan du plocka fram färdiga mallar eller skriva matematiken som LaTex.
Nedan hittar du några användbara kommandon i LaTex som, eventuellt, försnabbar processen att skriva matematik på dator.
| Vad? | Kommando | Hur det ser ut |
|---|---|---|
| Division | \dfrac{1}{2} eller \frac{1}{2} | \( \dfrac{1}{2} \) eller \(\frac{1}{2}\) |
| Upphöjt | x^2, eller x^{-2} | \( x^2 \) eller \( x^{-2} \) |
| Upphöjt med bråk | x^{\frac{1}{2}} | \( x^{\frac{1}{2}} \) |
| Kvadratrot | \sqrt{4} | \( \sqrt{4} \) |
| n:te rot | \sqrt[n]{4} | \( \sqrt[n]{4} \) |
| Logaritm, bas a | \log_a | \( \log_a \) |
| Logaritm, bas e | \ln | \( \ln \) |
| Summa | \sum_{i=1}^{10} | \( \sum_{i=1}^{10} \) |
| Vektorbeteckning med pil | \overrightarrow{a} | \( \overrightarrow{a} \) |
| Vektorbeteckning med linje | \overline{a} | \( \overline{a} \) |
| Sinus, cosinuns och tangens | \sin, \cos och \tan | \( \sin, \cos \) och \( \tan \) |
| Derivata | D | \( D \) |
| Integralbeteckning | \int_a^b | \( \int_a^b \) |
| Integralbeteckning, slutet | \text{ d}x | \( \text{ d}x \) |
| Integralbeteckning, raka sträcket | \big/_a^b | \( \big/_a^b \) |